【C++动态规划】有效括号的嵌套深度
本文涉及知识点
C++动态规划
LeetCode1111. 有效括号的嵌套深度
有效括号字符串 定义:对于每个左括号,都能找到与之对应的右括号,反之亦然。详情参见题末「有效括号字符串」部分。
嵌套深度 depth 定义:即有效括号字符串嵌套的层数,depth(A) 表示有效括号字符串 A 的嵌套深度。详情参见题末「嵌套深度」部分。
有效括号字符串类型与对应的嵌套深度计算方法如下图所示:
给你一个「有效括号字符串」 seq,请你将其分成两个不相交的有效括号字符串,A 和 B,并使这两个字符串的深度最小。
不相交:每个 seq[i] 只能分给 A 和 B 二者中的一个,不能既属于 A 也属于 B 。
A 或 B 中的元素在原字符串中可以不连续。
A.length + B.length = seq.length
深度最小:max(depth(A), depth(B)) 的可能取值最小。
划分方案用一个长度为 seq.length 的答案数组 answer 表示,编码规则如下:
answer[i] = 0,seq[i] 分给 A 。
answer[i] = 1,seq[i] 分给 B 。
如果存在多个满足要求的答案,只需返回其中任意 一个 即可。
示例 1:
输入:seq = “(()())”
输出:[0,1,1,1,1,0]
示例 2:
输入:seq = “()(())()”
输出:[0,0,0,1,1,0,1,1]
解释:本示例答案不唯一。
按此输出 A = “()()”, B = “()()”, max(depth(A), depth(B)) = 1,它们的深度最小。
像 [1,1,1,0,0,1,1,1],也是正确结果,其中 A = “()()()”, B = “()”, max(depth(A), depth(B)) = 1 。
提示:
1 < seq.size <= 10000
有效括号字符串:
仅由 “(” 和 “)” 构成的字符串,对于每个左括号,都能找到与之对应的右括号,反之亦然。
下述几种情况同样属于有效括号字符串:
-
空字符串
-
连接,可以记作 AB(A 与 B 连接),其中 A 和 B 都是有效括号字符串
-
嵌套,可以记作 (A),其中 A 是有效括号字符串
嵌套深度:
类似地,我们可以定义任意有效括号字符串 s 的 嵌套深度 depth(S): -
s 为空时,depth(“”) = 0
-
s 为 A 与 B 连接时,depth(A + B) = max(depth(A), depth(B)),其中 A 和 B 都是有效括号字符串
-
s 为嵌套情况,depth(“(” + A + “)”) = 1 + depth(A),其中 A 是有效括号字符串
例如:“”,“()()”,和 “()(()())” 都是有效括号字符串,嵌套深度分别为 0,1,2,而 “)(” 和 “(()” 都不是有效括号字符串。
简化后的问题:求最小max(a的深度,b的深度)
和本题没直接关系,类似而已。本方法可以求解,只是太麻烦。
如果s[i]为左括号,其权值为1;为右括号,其权值为-1。p[i]记录s[0…i]的权值和。
pa[i]记录s[0…i]中被a选中的权值和。pb[i]记录s[0…i]中被b选中的权值和。
根据括号的等效条件:
条件一, ∀ \forall ∀i,p[i],pa[i],pb[i]都>=0。
条件二:p.back() pa.back() pb.back()都为0。
令f(left,right) 记录s[left…right]中被拆分A,B部分,的最大深度。
推论一:如p[i]等于0,则s[0…i]和s[i+1…n-1]都是合法括号。
推论二:如p[i]等于0,则pa[i]和pb[i]都等于0,即a,b都可以通过s[i]拆分。
推论三:如果s[i] ==0 ,则f(0,n-1) = max(f(0,i),f(i+1,n-1))。
令 11,i2 = g(left,right) 记录s[left…right],i1是A的深度,i2是b的深度。确保max(i1,i2)最小。
推论四:除了p.back()外p[i]全大于0,则
i3,i4 = g(left+1,right-1) , i1 = min(i3,i4)+1 i2 = max(i3,i4)
如果left > right,则返回{0,0}
时间复杂度:O(nn) ∀ \forall ∀i,每层s[i]都只会处理一次。
代码
class Solution {public:int maxDepthAfterSplit(string seq){function<pair<int,int>(int,int)> Do = [&](int left, int right)-> pair<int, int> {if (left > right) { return make_pair(0,0); }int cur = 0;for (int i = left; i < right; i++) {cur += ('(' == seq[i]) ? 1 : -1;if (cur == 0) { auto [i1, i2] = Do(left,i);auto [i3, i4] = Do(i+1, right);vector<int> is = { i1,i2,i3,i4 };sort(is.begin(), is.end());return { is[1] ,is.back() };}}auto [i1, i2] = Do(left+1,right-1);return { min(i1,i2) + 1,max(i1,i2) };};auto [i1, i2] = Do(0, seq.length() - 1);return max(i1, i2);}};
单元测试
string seq;TEST_METHOD(TestMethod1){seq = "(())";auto res = Solution().maxDepthAfterSplit(seq);AssertEx(1, res);}TEST_METHOD(TestMethod11){seq = "(()())";auto res = Solution().maxDepthAfterSplit(seq);AssertEx(1, res);}TEST_METHOD(TestMethod12){seq = "()(())()";auto res = Solution().maxDepthAfterSplit(seq);AssertEx(1, res);}
栈
如果用栈判断一个字符串是否是合法括号
左括号入栈。遇到右括号,消掉栈顶的左括号,如果栈为空则非法。最终栈顶应该为空,否则非法。
a,b两个栈分别记录两个子序列,遇到左括号,放到元素少的栈。遇到右括号,消除栈顶元素多的栈。
我们只需要知道栈的元素数量,故可以ca,cb记录两者的数量。
时间复杂度:O(n)
代码
class Solution {public:vector<int> maxDepthAfterSplit(string seq) {int ca = 0,cb=0;const int N = seq.length();vector<int> ret(N);for (int i = 0; i < N;i++ ) {if ('(' == seq[i]) {if (ca < cb) {ca++;ret[i] = 0;}else {cb++;ret[i] = 1;}}else {if (ca > cb) {ca--;ret[i] = 0;}else {cb--;ret[i] = 1;}}}return ret;}};
单元测试
int MaxDeq(const string& s) {int ret = 0,cur=0;for (const auto& ch : s){cur += ('(' == ch) ? 1 : -1;ret = max(ret, cur);}return ret;}int Res(const string& s, const vector<int>& res) {string s1, s2;for (int i = 0; i < s.length(); i++) {if (res[i]) {s1 += s[i];}else {s2 += s[i];}}return max(MaxDeq(s1), MaxDeq(s2));}string seq;TEST_METHOD(TestMethod1){seq = "(())";auto res = Solution().maxDepthAfterSplit(seq);AssertEx(1, Res(seq, res));}TEST_METHOD(TestMethod11){seq = "(()())";auto res = Solution().maxDepthAfterSplit(seq);AssertEx(1, Res(seq, res));}TEST_METHOD(TestMethod12){seq = "()(())()";auto res = Solution().maxDepthAfterSplit(seq);AssertEx(1, Res(seq, res));}

扩展阅读
| 我想对大家说的话 |
|---|
| 工作中遇到的问题,可以按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 学习算法:按章节学习《喜缺全书算法册》,大量的题目和测试用例,打包下载。重视操作 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
| 失败+反思=成功 成功+反思=成功 |
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【C++动态规划】有效括号的嵌套深度
本文涉及知识点 C动态规划 LeetCode1111. 有效括号的嵌套深度 有效括号字符串 定义:对于每个左括号,都能找到与之对应的右括号,反之亦然。详情参见题末「有效括号字符串」部分。 嵌套深度 depth 定义:即有效括号字符串嵌套的层…...
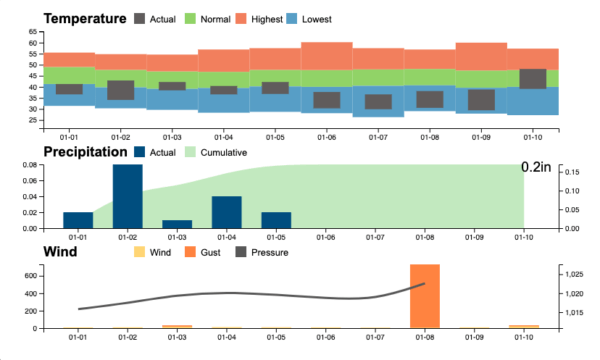
2024年优秀的天气预测API
准确、可操作的天气预报对于许多组织的成功至关重要。 事实上,在整个行业中,天气条件会直接影响日常运营,包括航运、按需、能源和供应链(仅举几例)。 以公用事业为例。根据麦肯锡的数据,在 1.4 年的时间里…...

Android和iOS有什么区别?
Android 和 iOS 有以下区别: 开发者与所属公司: Android:由谷歌公司开发以及开放手机联盟维护。它是基于 Linux 内核和其他开源软件的修改版本,代码开源程度较高,许多厂商都可以基于 Android 源代码进行深度定制和开发…...

NVR小程序接入平台/设备EasyNVR多个NVR同时管理多平台级联与上下级对接的高效应用
政务数据共享平台的建设正致力于消除“信息孤岛”现象,打破“数据烟囱”,实现国家、省、市及区县数据的全面对接与共享。省市平台的“级联对接”工作由多级平台共同构成,旨在满足跨部门、跨层级及跨省数据共享的需求,推动数据流通…...

Spring Cloud Sleuth(Micrometer Tracing +Zipkin)
分布式链路追踪 分布式链路追踪技术要解决的问题,分布式链路追踪(Distributed Tracing),就是将一次分布式请求还原成调用链路,进行日志记录,性能监控并将一次分布式请求的调用情况集中展示。比如各个服务节…...

人工智能:机遇与挑战
人工智能(AI)作为当今世界科技发展的前沿领域,正在以前所未有的速度和规模影响着我们的生活和工作方式。AI技术的应用前景广阔,从医疗健康到金融服务,从教育到交通,再到娱乐和家庭生活,AI正在逐…...

mac电脑设置crontab定时任务,以及遇到的问题解决办法
crontab常用命令 crontab -u user:用来设定某个用户的crontab服务; crontab file:file是命令文件的名字,表示将file做为crontab的任务列表文件并载入crontab。如果在命令行中没有指定这个文件,crontab命令将接受标准输入…...

Backtrader 数据篇 02
Backtrader 数据篇 本系列是使用Backtrader在量化领域的学习与实践,着重介绍Backtrader的使用。Backtrader 中几个核心组件: Cerebro:BackTrader的基石,所有的操作都是基于Cerebro的。Feed:将运行策略所需的基础数据…...

视频转场素材资源网站分享
视频剪辑者常常为找不到合适的转场素材而苦恼。合适的转场素材能让视频更流畅,给观众带来惊喜。下面就为大家介绍几个宝藏网站,提供丰富的转场剪辑素材,让你的视频瞬间高大上。 蛙学网 首先重磅推荐蛙学网,堪称视频素材界的“翘楚…...

二十二、MySQL 8.0 主从复制原理分析与实战
文章目录 一、复制(Replication)1、什么是复制2、复制的方式3、复制的数据同步类型3.1、异步复制3.2、半同步复制3.3、设计理念:复制状态机——几乎所有的分布式存储都是这么复制数据的 4、基于binlog位点同步的主从复制原理4.1、异步复制示例…...

基于OSS搭建在线教育视频课程分享网站
OSS对象存储服务是海量、安全、低成本、高持久的存储服务。适合于存储大规模非结构化数据,如图片、视频、备份文件和容器/虚拟机镜像等。 安装nginx wget https://nginx.org/download/nginx-1.20.2.tar.gz yum -y install zlib zlib-devel gcc-c pcre-devel open…...

CentOS 7 下升级 OpenSSL
升级openssh,下载:https://download.csdn.net/download/weimeilayer/89935114 上传到服务器,然后执行命令 rpm -Uvh *.rpm --nodeps --force安装依赖 yum -y install gcc perl make zlib-devel perl-CPAN下载安装包:https://github.com/ope…...

线上 Dump
优质博文:IT-BLOG-CN 一、简介 机器宕机或者请求很慢最常出现的几种问题:针对代码bug或者qps过高造成的。 【1】cpu过高致内存耗尽OOM,堆区对象回收不及时cpu被打满 【2】死锁抢用资源导致cpu过高致耗尽 【3】内存泄漏: 堆内存由…...
AcWing 1303:斐波那契前 n 项和 ← 矩阵快速幂加速递推
【题目来源】https://www.acwing.com/problem/content/1305/http://poj.org/problem?id3070【题目描述】 大家都知道 数列吧,。现在问题很简单,输入 和 ,求 的前 项和 。【输入格式】 共一行,包含两个整数 和 。【输出格式】…...

2024 Rust现代实用教程:1.2编译器与包管理工具以及开发环境搭建
文章目录 一、Rust的编译器rustc二、开发环境搭建三、Rust的包管理工具Cargo四、项目结构1.Cargo.toml文件2.创建一个可执行文件项目3.创建一个库项目 参考 一、Rust的编译器rustc 查看版本 rustc-version编译生成二进制文件 rustc -o output filename filename.rs编译生成库…...

人工智能原理实验一:知识的表示与推理实验
一、实验目的 本实验课程是计算机、智能、物联网等专业学生的一门专业课程,通过实验,帮助学生更好地掌握人工智能相关概念、技术、原理、应用等;通过实验提高学生编写实验报告、总结实验结果的能力;使学生对智能程序、智能算法等有…...

自学C语言——VS实用调试技巧总结
接上一篇:自学C语言——扫雷游戏(无递归) 什么是bug “bug”本意是昆虫或虫子,一般指电脑系统或程序中,隐藏着一些未被发现的缺陷或者问题,简称程序漏洞。 第一代的计算机是由许多庞大且昂贵的真空管组成&…...

VC2012创建弹出式菜单
首先为视类添加鼠标右键单击处理函数,添加如下代码, void CMFCApplication1View::OnRButtonDown(UINT nFlags, CPoint point) {// TODO: 在此添加消息处理程序代码和/或调用默认值CView::OnRButtonDown(nFlags, point);CMenu menu;menu.CreatePopupMenu…...

Google 第三季度季报出炉
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
)
入职总结(更新中)
【STEP 1/3】短信1之后:材料准备阶段 填写 新进教职工“入职一件事”线上办理 系统档案转递证明(需档案到校); 档案:为规范管理,请拟报到人员将个人档案寄至浙江财经大学人事处,有专职人员进行…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
