AcWing 1303:斐波那契前 n 项和 ← 矩阵快速幂加速递推
【题目来源】
https://www.acwing.com/problem/content/1305/
http://poj.org/problem?id=3070
【题目描述】
大家都知道 数列吧,
。现在问题很简单,输入
和
,求
的前
项和
。
【输入格式】
共一行,包含两个整数 和
。
【输出格式】
输出前 项和
的值。
【数据范围】
【输入样例】
5 1000
【输出样例】
12
【算法分析】
★ 矩阵快速幂加速递推
(1)已知 数列递推式为
,但当
极大时,会超时。
故基于“矩阵快速幂加速递推”的思路,改写数列递推式 为
改写后的递推式对应的 LaTex 代码为:
[F_n \quad F_{n-1}]=[F_{n-1} \quad F_{n-2}]
\begin{bmatrix}
1 & 1\\
1 & 0
\end{bmatrix}
=[F_{n-2} \quad F_{n-3}]
\begin{bmatrix}
1 & 1\\
1 & 0
\end{bmatrix}
\begin{bmatrix}
1 & 1\\
1 & 0
\end{bmatrix}
=\cdots =[F_1,F_0]
\begin{bmatrix}
1 & 1\\
1 & 0
\end{bmatrix}^{n-1}(2)若令 ,则有
。
据此公式可知,首先求出 ,然后用
左乘,便可得到
,而
的第一个元素即为
。注意:标红的公式,技巧在于使用了 LaTex 命令: \textcolor{red} {公式}
\textcolor{red} {X_n=X_1\times A^{n-1}}
★ 矩阵快速幂模板:https://blog.csdn.net/hnjzsyjyj/ar左乘ticle/details/143227091
【算法代码】
#include<bits/stdc++.h>
using namespace std;typedef long long LL;
LL A[2][2]= {{1,1},{1,0}
};
LL ans[2]= {1,0}; //save answerint n,m;//Column matrix A * matrix B
void mul1(LL A[], LL B[][2]) {LL t[2]= {0};for(int i=0; i<2; i++)for(int j=0; j<2; j++)t[i]+=A[j]*B[i][j]%m;for(int i=0; i<2; i++)A[i]=t[i]%m;
}//matrix A * matrix B
void mul2(LL A[][2], LL B[][2]) {LL t[2][2]= {0};for(int i=0; i<2; i++)for(int j=0; j<2; j++)for(int k=0; k<2; k++)t[i][j]+=A[i][k]*B[k][j]%m;for(int i=0; i<2; i++)for(int j=0; j<2; j++)A[i][j]=t[i][j]%m;
}int main() {scanf("%d%d",&n,&m);n+=2; //get f[n+2]while(n) { //fastPowif(n & 1) mul1(ans,A);mul2(A,A);n>>=1;}printf("%lld\n", ans[1]-1); //ans[1] is f[n+2]return 0;
}/*
in:
5 1000out:
12
*/
【参考文献】
https://www.acwing.com/blog/content/25/
https://blog.csdn.net/hnjzsyjyj/article/details/143227091
https://www.cnblogs.com/yijiull/p/6641422.html
https://www.acwing.com/solution/content/15121/
相关文章:
AcWing 1303:斐波那契前 n 项和 ← 矩阵快速幂加速递推
【题目来源】https://www.acwing.com/problem/content/1305/http://poj.org/problem?id3070【题目描述】 大家都知道 数列吧,。现在问题很简单,输入 和 ,求 的前 项和 。【输入格式】 共一行,包含两个整数 和 。【输出格式】…...

2024 Rust现代实用教程:1.2编译器与包管理工具以及开发环境搭建
文章目录 一、Rust的编译器rustc二、开发环境搭建三、Rust的包管理工具Cargo四、项目结构1.Cargo.toml文件2.创建一个可执行文件项目3.创建一个库项目 参考 一、Rust的编译器rustc 查看版本 rustc-version编译生成二进制文件 rustc -o output filename filename.rs编译生成库…...

人工智能原理实验一:知识的表示与推理实验
一、实验目的 本实验课程是计算机、智能、物联网等专业学生的一门专业课程,通过实验,帮助学生更好地掌握人工智能相关概念、技术、原理、应用等;通过实验提高学生编写实验报告、总结实验结果的能力;使学生对智能程序、智能算法等有…...

自学C语言——VS实用调试技巧总结
接上一篇:自学C语言——扫雷游戏(无递归) 什么是bug “bug”本意是昆虫或虫子,一般指电脑系统或程序中,隐藏着一些未被发现的缺陷或者问题,简称程序漏洞。 第一代的计算机是由许多庞大且昂贵的真空管组成&…...

VC2012创建弹出式菜单
首先为视类添加鼠标右键单击处理函数,添加如下代码, void CMFCApplication1View::OnRButtonDown(UINT nFlags, CPoint point) {// TODO: 在此添加消息处理程序代码和/或调用默认值CView::OnRButtonDown(nFlags, point);CMenu menu;menu.CreatePopupMenu…...

Google 第三季度季报出炉
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
)
入职总结(更新中)
【STEP 1/3】短信1之后:材料准备阶段 填写 新进教职工“入职一件事”线上办理 系统档案转递证明(需档案到校); 档案:为规范管理,请拟报到人员将个人档案寄至浙江财经大学人事处,有专职人员进行…...

@DeleteMapping和@PostMapping和@GetMapping和Content-Type使用记录
代码例子,有注释大家可以自己试一下 RestController RequestMapping(value "demo") public class TestController {//Content-Type:application/x-www-form-urlencoded;表单提交form-dataPostMapping("/demo1")public String test…...
unity 中使用zeroMq和Mqtt 进行通讯
最近我在做一个车上的HMI项目,也就是车机应用,需要与云端和域控进行通信。HMI的功能已经外包了,但消息的统一层留给我自己来做。因为项目组其他人都没有经验,所以这个任务就落到了我头上,尽管我自己也没有太多经验&…...
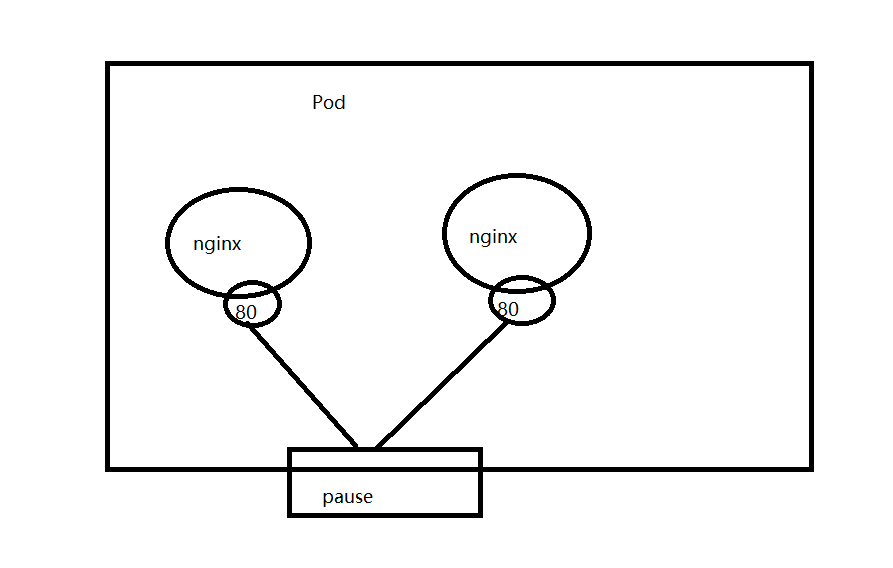
四、k8s快速入门之Kubernetes资源清单
kubernetes中的资源 ⭐️ k8s中所有的内容都抽象为资源,资源实列化之后,叫做对象 1️⃣名称空间级别 ⭐️ kubeadm在执行k8s的pod的时候会在kube-system这个名称空间下执行,所以说当你kubectl get pod 的时候是查看不到的查看的是默认的po…...

掌握ElasticSearch(六):分析过程
文章目录 一、什么是分析1. 字符过滤 (Character Filtering)2. 分词 (Breaking into Tokens)3. 词条过滤 (Token Filtering)4. 词条索引 (Token Indexing) 二、内置分析器分类1. 标准分析器 (Standard Analyzer)2. 简单分析器 (Simple Analyzer)3. 语言分析器 (Language Analyz…...

【设计模式】使用python 实践框架设计
单一职责原则(SRP):一个类应该只有一个职责,意味着该类只应该有一个引起变化的原因。这使得代码更易于维护和理解。 开放封闭原则(OCP):软件实体(类、模块、函数等)应该…...

Apache paimon-CDC
CDC集成 paimon支持五种方式通过模式转化数据提取到paimon表中。添加的列会实时同步到Paimon表中 MySQL同步表:将MySQL中的一张或多张表同步到一张Paimon表中。MySQL同步数据库:将MySQL的整个数据库同步到一个Paimon数据库中。API同步表:将您的自定义DataStream输入同步到一…...

如何分析算法的执行效率和资源消耗
分析算法的执行效率和资源消耗可以从以下几个方面入手: 一、时间复杂度分析 定义和概念 时间复杂度是衡量算法执行时间随输入规模增长的速度的指标。它通常用大 O 符号表示,表示算法执行时间与输入规模之间的关系。例如,一个算法的时间复杂度为 O(n),表示该算法的执行时间…...

提示工程(Prompt Engineering)指南(进阶篇)
在 Prompt Engineering 的进阶阶段,我们着重关注提示的结构化、复杂任务的分解、反馈循环以及模型的高级特性利用。随着生成式 AI 技术的快速发展,Prompt Engineering 已经从基础的单一指令优化转向了更具系统性的设计思维,并应用于多轮对话、…...
——FFmpeg源码中,解码Audio Tag的AudioTagHeader,并提取AUDIODATA的实现)
音视频入门基础:FLV专题(19)——FFmpeg源码中,解码Audio Tag的AudioTagHeader,并提取AUDIODATA的实现
一、引言 从《音视频入门基础:FLV专题(18)——Audio Tag简介》可以知道,未加密的情况下,FLV文件中的一个Audio Tag Tag header AudioTagHeader AUDIODATA。本文讲述FFmpeg源码中是怎样解码Audio Tag的AudioTagHead…...

前端零基础入门到上班:【Day3】从零开始构建网页骨架HTML
HTML 基础入门:从零开始构建网页骨架 目录 1. 什么是 HTML?HTML 的核心作用 2. HTML 基本结构2.1 DOCTYPE 声明2.2 <html> 标签2.3 <head> 标签2.4 <body> 标签 3. HTML 常用标签详解3.1 标题标签3.2 段落和文本标签3.3 链接标签3.4 图…...

字符脱敏工具类
1、字符脱敏工具类 import lombok.extern.slf4j.Slf4j; import org.apache.commons.lang3.StringUtils;/*** 数据脱敏工具类** date 2024/10/30 13:44*/Slf4j public class DataDesensitizationUtils {public static final String STAR_1 "*";public static final …...

【jvm】jvm对象都分配在堆上吗
目录 1. 说明2. 堆上分配3. 栈上分配(逃逸分析和标量替换)4. 方法区分配5. 直接内存(非堆内存) 1. 说明 1.JVM的对象并不总是分配在堆上。2.堆是JVM用于存储对象实例的主要内存区域,存在一些特殊情况,对象…...

@AutoWired和 @Resource原理深度分析!
嗨,你好呀,我是猿java Autowired和Resource是 Java程序员经常用来实现依赖注入的两个注解,这篇文章,我们将详细分析这两个注解的工作原理、使用示例和它们之间的对比。 依赖注入概述 依赖注入是一种常见的设计模式,…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

World-writable config file /etc/mysql/mysql.conf.d/my.cnf is ignored
https://stackoverflow.com/questions/53741107/mysql-in-docker-on-ubuntu-warning-world-writable-config-file-is-ignored 修改权限 -> 重启mysql # 检查字符集配置 SHOW VARIABLES WHERE Variable_name IN (character_set_server, character_set_database ); --------…...

【仿生机器人】刀剑神域——爱丽丝苏醒计划,需求文档
仿生机器人"爱丽丝"系统架构设计需求文档 一、硬件基础 已完成头部和颈部硬件搭建 25个舵机驱动表情系统 颈部旋转功能 眼部摄像头(视觉输入) 麦克风阵列(听觉输入) 颈部发声装置(语音输出)…...

Java在word中指定位置插入图片。
Java使用(Poi-tl) 在word(docx)中指定位置插入图片 Poi-tl 简介Maven 依赖配置Poi-tl 实现原理与步骤1. 模板标签规范2.完整实现代码3.效果展示 Poi-tl 简介 Poi-tl 是基于 Apache POI 的 Java 开源文档处理库,专注于…...
