如何分析算法的执行效率和资源消耗
分析算法的执行效率和资源消耗可以从以下几个方面入手:
一、时间复杂度分析
-
定义和概念
- 时间复杂度是衡量算法执行时间随输入规模增长的速度的指标。它通常用大 O 符号表示,表示算法执行时间与输入规模之间的关系。
- 例如,一个算法的时间复杂度为 O(n),表示该算法的执行时间与输入规模 n 成正比;一个算法的时间复杂度为 O(log n),表示该算法的执行时间与输入规模 n 的对数成正比。
-
计算方法
- 计算算法的时间复杂度通常需要分析算法的执行流程,确定算法中每个操作的执行次数与输入规模之间的关系。
- 例如,对于一个简单的循环算法,其时间复杂度通常取决于循环的次数。如果循环的次数与输入规模 n 成正比,那么该算法的时间复杂度为 O(n)。
- 对于一些复杂的算法,可能需要使用数学归纳法、递归树等方法来计算时间复杂度。
-
常见时间复杂度类型
- 常见的时间复杂度类型包括 O(1)(常数时间复杂度)、O(log n)(对数时间复杂度)、O(n)(线性时间复杂度)、O(n log n)(线性对数时间复杂度)、O(n²)(平方时间复杂度)等。
- 不同的时间复杂度类型在不同的输入规模下表现
相关文章:

如何分析算法的执行效率和资源消耗
分析算法的执行效率和资源消耗可以从以下几个方面入手: 一、时间复杂度分析 定义和概念 时间复杂度是衡量算法执行时间随输入规模增长的速度的指标。它通常用大 O 符号表示,表示算法执行时间与输入规模之间的关系。例如,一个算法的时间复杂度为 O(n),表示该算法的执行时间…...

提示工程(Prompt Engineering)指南(进阶篇)
在 Prompt Engineering 的进阶阶段,我们着重关注提示的结构化、复杂任务的分解、反馈循环以及模型的高级特性利用。随着生成式 AI 技术的快速发展,Prompt Engineering 已经从基础的单一指令优化转向了更具系统性的设计思维,并应用于多轮对话、…...
——FFmpeg源码中,解码Audio Tag的AudioTagHeader,并提取AUDIODATA的实现)
音视频入门基础:FLV专题(19)——FFmpeg源码中,解码Audio Tag的AudioTagHeader,并提取AUDIODATA的实现
一、引言 从《音视频入门基础:FLV专题(18)——Audio Tag简介》可以知道,未加密的情况下,FLV文件中的一个Audio Tag Tag header AudioTagHeader AUDIODATA。本文讲述FFmpeg源码中是怎样解码Audio Tag的AudioTagHead…...

前端零基础入门到上班:【Day3】从零开始构建网页骨架HTML
HTML 基础入门:从零开始构建网页骨架 目录 1. 什么是 HTML?HTML 的核心作用 2. HTML 基本结构2.1 DOCTYPE 声明2.2 <html> 标签2.3 <head> 标签2.4 <body> 标签 3. HTML 常用标签详解3.1 标题标签3.2 段落和文本标签3.3 链接标签3.4 图…...

字符脱敏工具类
1、字符脱敏工具类 import lombok.extern.slf4j.Slf4j; import org.apache.commons.lang3.StringUtils;/*** 数据脱敏工具类** date 2024/10/30 13:44*/Slf4j public class DataDesensitizationUtils {public static final String STAR_1 "*";public static final …...

【jvm】jvm对象都分配在堆上吗
目录 1. 说明2. 堆上分配3. 栈上分配(逃逸分析和标量替换)4. 方法区分配5. 直接内存(非堆内存) 1. 说明 1.JVM的对象并不总是分配在堆上。2.堆是JVM用于存储对象实例的主要内存区域,存在一些特殊情况,对象…...

@AutoWired和 @Resource原理深度分析!
嗨,你好呀,我是猿java Autowired和Resource是 Java程序员经常用来实现依赖注入的两个注解,这篇文章,我们将详细分析这两个注解的工作原理、使用示例和它们之间的对比。 依赖注入概述 依赖注入是一种常见的设计模式,…...

C++设计模式创建型模式———原型模式
文章目录 一、引言二、原型模式三、总结 一、引言 与工厂模式相同,原型模式(Prototype)也是创建型模式。原型模式通过一个对象(原型对象)克隆出多个一模一样的对象。实际上,该模式与其说是一种设计模式&am…...
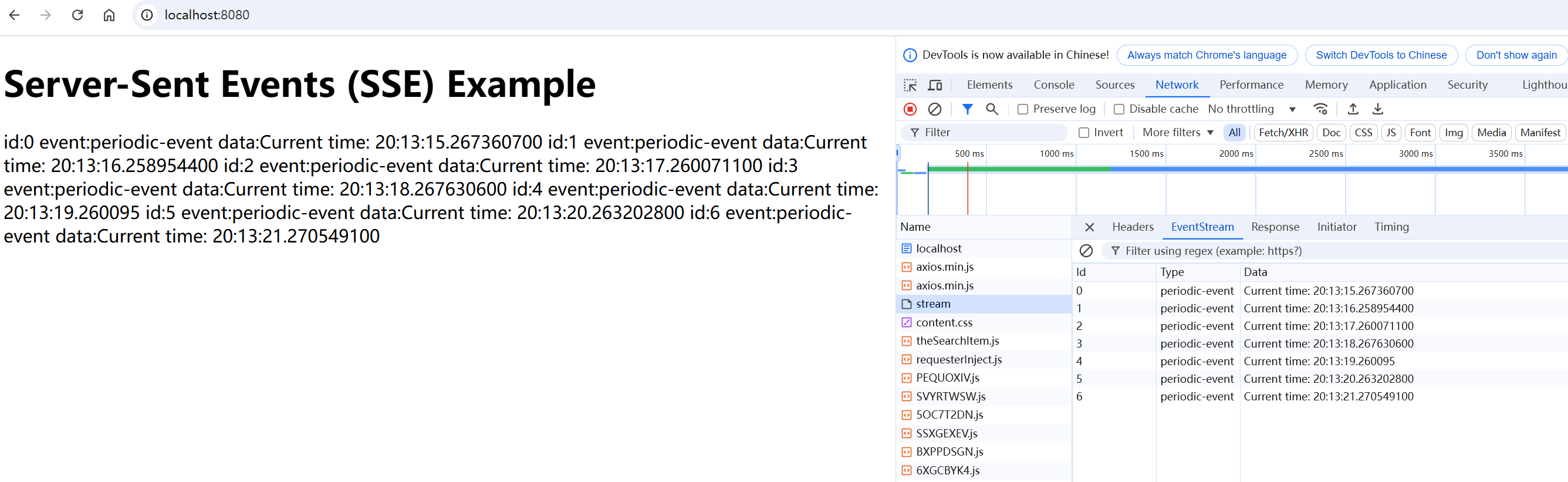
重学SpringBoot3-Spring WebFlux之SSE服务器发送事件
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ Spring WebFlux之SSE服务器发送事件 1. 什么是 SSE?2. Spring Boot 3 响应式编程与 SSE为什么选择响应式编程实现 SSE? 3. 实现 SSE 的基本步骤3.…...

YOLO即插即用模块---AgentAttention
Agent Attention: On the Integration of Softmax and Linear Attention 论文地址:https://arxiv.org/pdf/2312.08874 问题: 普遍使用的 Softmax 注意力机制在视觉 Transformer 模型中计算复杂度过高,限制了其在各种场景中的应用。 方法&a…...

探索开源语音识别的未来:高效利用先进的自动语音识别技术20241030
🚀 探索开源语音识别的未来:高效利用自动语音识别技术 🌟 引言 在数字化时代,语音识别技术正在引领人机交互的新潮流,为各行业带来了颠覆性的改变。开源的自动语音识别(ASR)系统,如…...

学习路之TP6--workman安装
一、安装 首先通过 composer 安装 composer require topthink/think-worker 报错: 分析:最新版本需要TP8,或装低版本的 composer require topthink/think-worker:^3.*安装后, 增加目录 vendor\workerman vendor\topthink\think-w…...

.NET内网实战:通过白名单文件反序列化漏洞绕过UAC
01阅读须知 此文所节选自小报童《.NET 内网实战攻防》专栏,主要内容有.NET在各个内网渗透阶段与Windows系统交互的方式和技巧,对内网和后渗透感兴趣的朋友们可以订阅该电子报刊,解锁更多的报刊内容。 02基本介绍 03原理分析 在渗透测试和红…...

AI Agents - 自动化项目:计划、评估和分配
Agents: Role 角色Goal 目标Backstory 背景故事 Tasks: Description 描述Expected Output 期望输出Agent 代理 Automated Project: Planning, Estimation, and Allocation Initial Imports 1.本地文件helper.py # Add your utilities or helper functions to…...

Git的.gitignore文件
一、各语言对应的.gitignore模板文件 项目地址:https://github.com/github/gitignore 二、.gitignore文件不生效 .gitignore文件只是ignore没有被追踪的文件,已被追踪的文件,要先删除缓存文件。 # 单个文件 git rm --cached file/path/to…...

网站安全,WAF网站保护暴力破解
雷池的核心功能 通过过滤和监控 Web 应用与互联网之间的 HTTP 流量,功能包括: SQL 注入保护:防止恶意 SQL 代码的注入,保护网站数据安全。跨站脚本攻击 (XSS):阻止攻击者在用户浏览器中执行恶意脚本。暴力破解防护&a…...

深度学习:梯度下降算法简介
梯度下降算法简介 梯度下降算法 我们思考这样一个问题,现在需要用一条直线来回归拟合这三个点,直线的方程是 y w ^ x b y \hat{w}x b yw^xb,我们假设斜率 w ^ \hat{w} w^是已知的,现在想要找到一个最好的截距 b b b。 一条…...

SparkSQL整合Hive后,如何启动hiveserver2服务
当spark sql与hive整合后,我们就无法启动hiveserver2的服务了,每次都要先启动hive的元数据服务(nohup hive --service metastore)才能启动hive,之前的beeline命令也用不了,hiveserver2的无法启动,这也导致我…...

前端路由如何从0开始配置?vue-router 的使用
在 Web 开发中,路由是指根据 URL 的不同部分将请求分发到不同的处理函数或页面的过程。路由是单页应用(SPA, Single Page Application)和服务器端渲染(SSR, Server-Side Rendering)应用中的一个重要概念。 在开发中如何…...

Java中的运算符【与C语言的区别】
目录 1. 算术运算符 1.0 赋值运算符: 1.1 四则运算符: - * / % 【取余与C有点不同】 1.2 增量运算符: - * / % * 【右侧运算结果会自动转换类型】 1.3 自增、自减:、-- 2. 关系运算符 3. 逻辑运算符 3.1 短路求值 3.2 【…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
