集合论(ZFC)之 选择公理(Axiom of Choice)注解
直观感受(Intuition)
集合论(ZFC)中的 "C" 指的是选择公理(Axiom of Choice)中的"choice"。简单来说,对于任一非空集合 S,那么存在一个函数 f,选择出其中的元素 s ∈ S,即 s = f(S) ∈ S。
形式化(Formalization)
正式定义有,对于任一索引非空集合族(indexed family of non-empty set),记,{Sᵢ: i ∈ I},其中,i for index。那么,存在一个索引集合,记,{xᵢ: i ∈ I},使得 ∀i∈I. (xᵢ ∈ Sᵢ)。
也就是说,存在一个选择函数 choice,使得,
∀i∈I. (choice( Sᵢ ∈ {Sᵢ: i ∈ I} ) ∈ Sᵢ )
其中,choice: {Sᵢ: i ∈ I} → Sᵢ
xᵢ = choice(Sᵢ)
注解(Annotation)
初步看来,其实挺合理的,就是,一个非空的集合,意味着,该集合肯定包含了某些元素,又,既然包含了一些元素,那么,肯定能选取出一个元素来。
可是,这里忽略了一点,就是,存在(existence)与能选出(choice)是两个区别的概念。而选择公理(Axiom of Choice)则规定了,只要是存在的(non-empty),那么,就能选出(choice),也就是,将这两概念等价起来了。
这样,通过选择公理(AC),可以证明一些不可构建(non-constructable)的存在(existence)。例如,最为形象的是,Banach–Tarski 悖论。由此,也引申出不可测量集合(non-measurable sets)的概念。
另外,选择公理(AC)隐含了(implies)排中律(Law of Excluded Middle),即,
AC → P∨¬P ≡ True
排中律,说的是,对于任一命题P,命题P为真,或∨,其反命题¬P为真。这里就产生了个有意思的逻辑。
对于命题连接符,或∨,来说,其输出的值,由其输入决定,即,对于A∨B来说,A、B中,有一个为真(True),那么,或∨的输出为真(True)。这里有明确的输入,产生明确的输出。即,需要证明A是真,或者,B是真,才能得出, A∨B 是真。
而对于排中律来说,不需要证明,P、¬P哪个是真,就能得出, P∨¬P 是真的。反过来说,当有 P∨¬P 为真,那么,通过 选择公理(AC),就能选择出其中为真的命题,是P,或则是¬P。即,
choice(P∨¬P) ∈ P∨¬P。
这里,合理解析为,如果P是真,那么¬P肯定不为真;反之亦然。也就是说,对于命题P来说,不管是否能证明,命题P的真值只有真(True)与假(False)。就相当于,只要是非空集合(P∨¬P),那肯定存在一个元素,无论是 P 或 ¬P ,那么,该元素就是 choice(P∨¬P) ,使得(P∨¬P)非空,即 (P∨¬P)恒为真。即,通过,choice(P∨¬P) ,证明,P∨¬P ≡ True 。
相关文章:
之 选择公理(Axiom of Choice)注解)
集合论(ZFC)之 选择公理(Axiom of Choice)注解
直观感受(Intuition) 集合论(ZFC)中的 "C" 指的是选择公理(Axiom of Choice)中的"choice"。简单来说,对于任一非空集合 S,那么存在一个函数 f,选择出…...

JS:字符串操作
目录 1、 字符串分割 1、 字符串分割 var str "123,456,789"; console.log(str.split(,)); // ["123", "456", "789"]...

.NET 一款二进制文件转换Shellcode的工具
01阅读须知 此文所提供的信息只为网络安全人员对自己所负责的网站、服务器等(包括但不限于)进行检测或维护参考,未经授权请勿利用文章中的技术资料对任何计算机系统进行入侵操作。利用此文所提供的信息而造成的直接或间接后果和损失…...

【CSS】——基础入门常见操作
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录 一:CSS引入 二:CSS对元素进行美化 1:style修饰 2:选…...
词法分析)
LuaJIT源码分析(五)词法分析
LuaJIT源码分析(五)词法分析 lua虽然是脚本语言,但在执行时,还是先将脚本编译成字节码,然后再由虚拟机解释执行。在编译脚本时,首先需要对源代码进行词法分析,把源代码分解为token流。lua的toke…...

005 匿名信
005 匿名信 题目描述 电视剧《分界线》里面有一个片段,男主为了向警察透露案件细节,且不暴露自己,于是将报刊上的字剪下来,剪拼成一封匿名信。现在有一名举报人,希望借鉴这种方式,使用英文报刊完成举报操…...

聊聊Web3D 发展趋势
随着 Web 技术的不断演进,Web3D 正逐渐成为各行业数字化的重要方向。Web3D 是指在网页中展示 3D 内容的技术集合。近年来,由于 WebGL、WebGPU 等技术的发展,3D 内容已经能够直接在浏览器中渲染,为用户提供更加沉浸、互动的体验。以…...

【数据结构与算法】LeetCode: 贪心算法
文章目录 LeetCode: 贪心算法买卖股票的最佳时机 (Hot100)买卖股票的最佳时机 II跳跃游戏 (Hot100)跳跃游戏 II(Hot100)划分字母区间 (Hot100)分发饼干K次取反后最大化的…...

Date 日期类的实现(c++)
本文用c实现日期类 将会实现以下函数 bool operator<(const Date& d);bool operator<(const Date& d);bool operator>(const Date& d);bool operator>(const Date& d);bool operator(const Date& d);bool operator!(const Date& d);Date&…...

智能家居10G雷达感应开关模块,飞睿智能uA级别低功耗、超高灵敏度,瞬间响应快
在当今科技飞速发展的时代,智能家居已经逐渐成为人们生活中不可或缺的一部分。从智能灯光控制到智能家电的联动,每一个细节都在为我们的生活带来便利和舒适。而在众多智能家居产品中,10G 雷达感应开关模块以其独特的优势,正逐渐成…...

头歌——人工智能(机器学习 --- 决策树2)
文章目录 第5关:基尼系数代码 第6关:预剪枝与后剪枝代码 第7关:鸢尾花识别代码 第5关:基尼系数 基尼系数 在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益率…...

一七一、React性能优化方式
在 React 中进行性能优化可以通过多种手段来减少渲染次数、优化渲染效率并减少内存消耗。以下是常见的性能优化方法及示例: 1. shouldComponentUpdate shouldComponentUpdate 是类组件中的生命周期方法,它可以让组件在判断是否需要重新渲染时ÿ…...

编写dockerfile生成镜像,并且构建容器运行
编写dockerfile生成镜像,并且构建容器运行 目录 编写dockerfile生成镜像,并且构建容器运行 概述 一、dockerfile文件详解 Dockerfile的基本结构 Dockerfile的常用指令 二、构建过程 概述 随着微服务应用越来越多,大家需要尽快掌握dock…...

Java项目练习——学生管理系统
1. 整体结构 代码实现了基本的学生管理系统功能,包括登录、注册、忘记密码、添加、删除、修改和查询学生信息。 使用了ArrayList来存储用户和学生信息。 使用了Scanner类来处理用户输入。 2. 主要功能模块 登录 (logIn):验证用户名和密码,…...

sqlserver、达梦、mysql的差异
差异项sqlserver达梦mysql单行注释---- 1、-- ,--后面带个空格 2、# 包裹对象名称,如表、表字段等 [tableName] "tableName"tableName表字段自增IDENTITY(1, 1)IDENTITY(1, 1)AUTO_INCREMENT二进制数据类型IMAGEIMAGE、BLOBBLOB 存储一个汉字需…...

Spring AOP(定义、使用场景、用法、3种事务、事务失效场景及解决办法、面试题)
目录 1. AOP定义? 2.常见的AOP使用场景: 3.Spring AOP用法 3.1 Spring AOP中的几个核心概念 3.1.1 切面、切点、通知、连接点 3.1.2 切点表达式AspectJ 3.2 使用 Spring AOP 的步骤总结 3.2.1 添加依赖: 3.2.2 定义切面和切点(切点和…...

Flutter鸿蒙next 封装对话框详解
✅近期推荐:求职神器 https://bbs.csdn.net/topics/619384540 🔥欢迎大家订阅系列专栏:flutter_鸿蒙next 💬淼学派语录:只有不断的否认自己和肯定自己,才能走出弯曲不平的泥泞路,因为平坦的大路…...
【项目实战】通过LLaMaFactory+Qwen2-VL-2B微调一个多模态医疗大模型
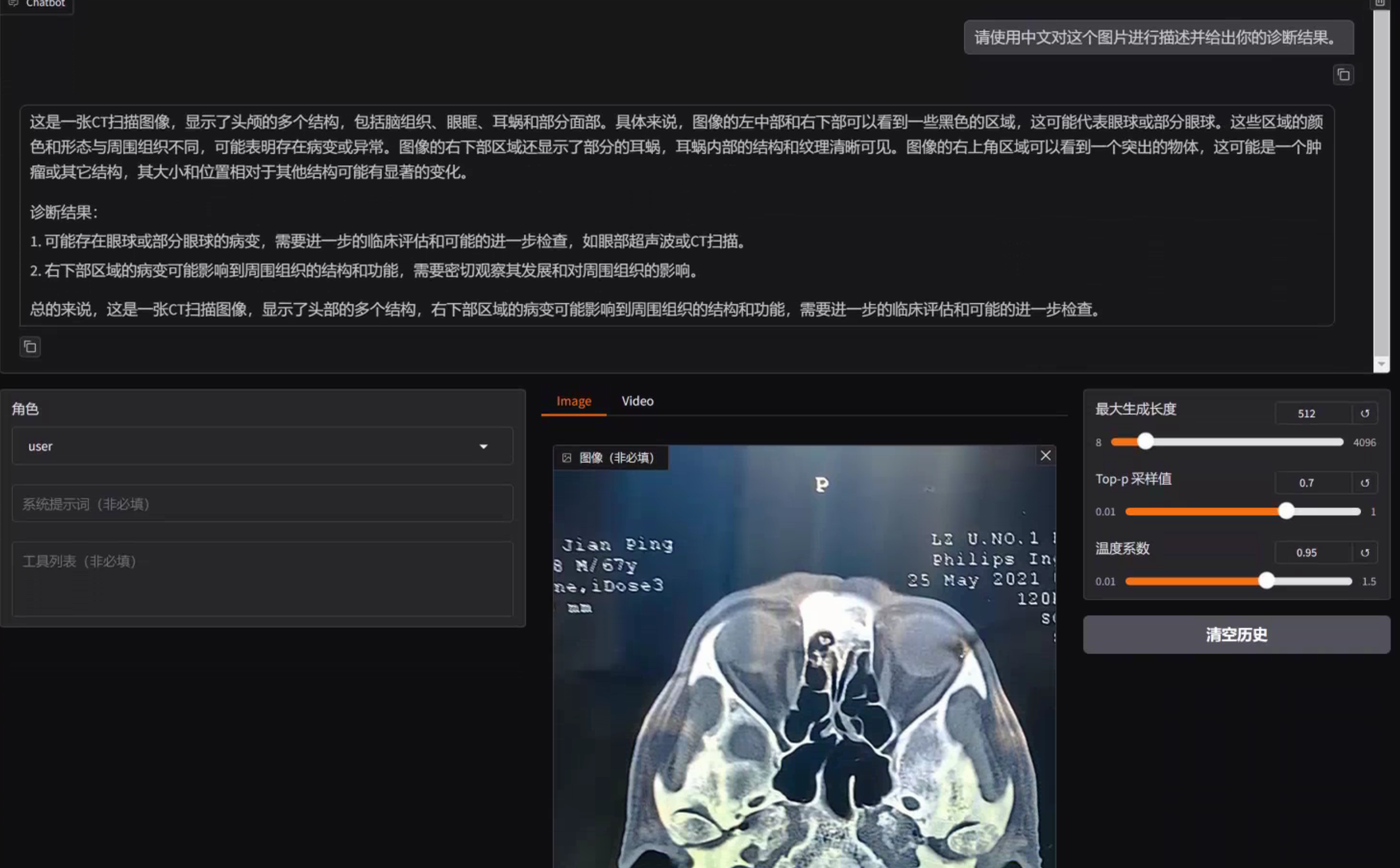
前言 随着多模态大模型的发展,其不仅限于文字处理,更能够在图像、视频、音频方面进行识别与理解。医疗领域中,医生们往往需要对各种医学图像进行处理,以辅助诊断和治疗。如果将多模态大模型与图像诊断相结合,那么这会…...

SCSI驱动与 UFS 驱动交互概况
SCSI子系统概况 SCSI(Small Computer System Interface)子系统是 Linux 中的一个模块化框架,用于提供与存储设备的通用接口。通过 SCSI 子系统,可以支持不同类型的存储协议(如 UFS、SATA、SAS),…...

软件工程实践项目:人事管理系统
一、项目的需求说明 通过移动设备登录app提供简单、方便的操作。根据公司原来的考勤管理制度,为公司不同管理层次提供相应的权限功能。通过app上面的各种标准操作,考勤管理无纸化的实现,使公司的考勤管理更加科学规范,从而节省考…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
