力扣判断字符是否唯一(位运算)
文章目录
- 给一个数n,判断它的二进制位中第x位是0还是1(从0开始计数)
- 将一个数n的二进制位第X位修改为1(从0开始计数)
- 将一个数n的二进制第x位修改为0(从0开始计数)
- 提取一个数n二进制中最右侧的1
- 去掉一个数n二进制表示中最右侧的1
今天我们通过判断字符是否唯一这个题来了解位运算的一些性质。
在做题之前我们需要先解决两个问题。
给一个数n,判断它的二进制位中第x位是0还是1(从0开始计数)

如果我们需要判断第4位是0还是1,我们只需要将n右移三位,然后和1按位与就可以了。
(n>>x)&1
先将n右移X位再按位与
将一个数n的二进制位第X位修改为1(从0开始计数)

实现方式:
n=n|(1<<x)
先将1左移X-1位再与n按位或
将一个数n的二进制第x位修改为0(从0开始计数)
实现方式:
n=n&(~(1<<x))
将1左移X-1位取反再按位与
大家可以自己举例子尝试
提取一个数n二进制中最右侧的1
实现方式:
n&(-n)
去掉一个数n二进制表示中最右侧的1
实现方式:
n&(n-1)
接下来运用上面的规律来解决判判断字符是否唯一这道题
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
示例 1:
输入: s = “leetcode”
输出: false
示例 2:
输入: s = “abc”
输出: true
限制:
0 <= len(s) <= 100
s[i]仅包含小写字母
如果你不使用额外的数据结构,会很加分。
解题思路:
因为只有26个小写字母,int 类型有32个比特位,所以我们可以将32个比特位看作一个哈希表(这个是思路有个名字叫位图),然后遍历字符串,如果字符第一次出现就将该字符对应的比特位改为1(例如字符‘a’对应的是0下标),没有出现的比特位就是0,这样我们只需要判断该字符对应的比特位是否是1,就可以判断字符串是否重复。
代码实现:
class Solution {public boolean isUnique(String astr) {int ret=0;if((astr.length())>26){return false;}char[] str=astr.toCharArray();for(char ch:str){int i=ch-'a';if(((ret>>i)&1)==1)//判断字符在之前是否出现过{return false;}ret|=1<<i;//字符第一次出现将对应的比特位初始为1}return true;}
}
大家有什么看法意见可以留言评论。
相关文章:

力扣判断字符是否唯一(位运算)
文章目录 给一个数n,判断它的二进制位中第x位是0还是1(从0开始计数)将一个数n的二进制位第X位修改为1(从0开始计数)将一个数n的二进制第x位修改为0(从0开始计数)提取一个数n二进制中最右侧的1去掉一个数n二进制表示中最右侧的1 今天我们通过判断字符是否唯一这个题来了解位运算…...
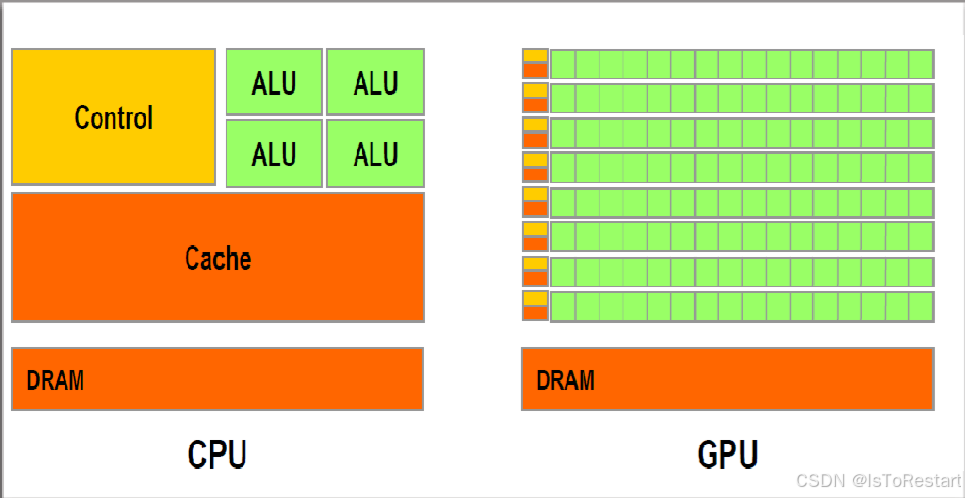
GPU和CPU区别?为什么挖矿、大模型都用GPU?
GPU(图形处理单元)和CPU(中央处理单元)是计算机中两种不同类型的处理器,它们在设计和功能上有很大的区别。 CPU是计算机的大脑,专门用于执行各种通用任务,如操作系统管理、数据处理、多任务处理等。它的架构设计旨在适应多种任务,…...
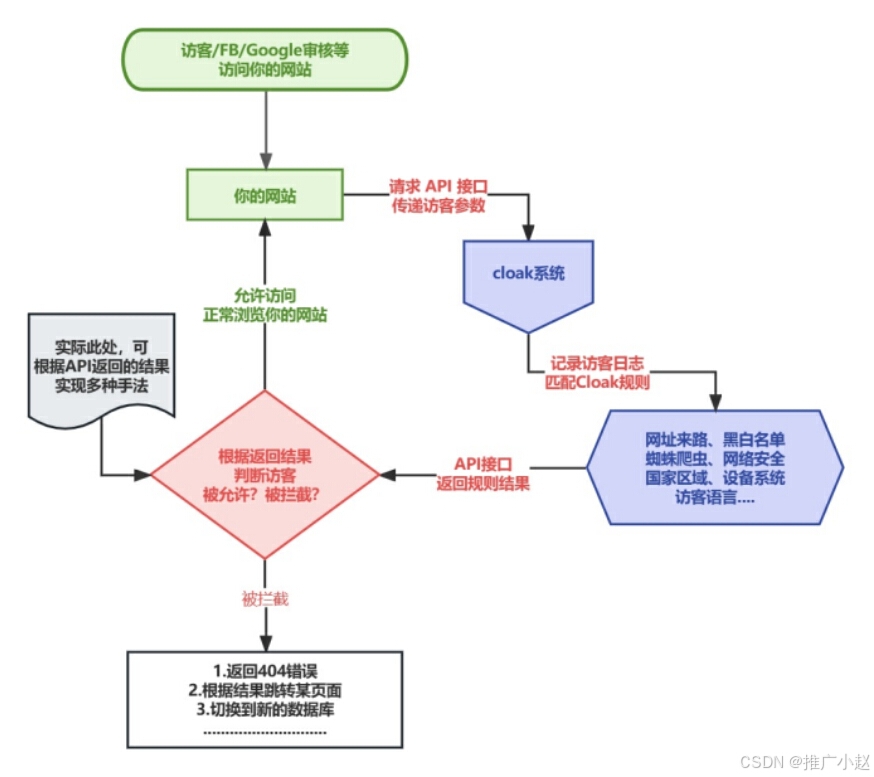
新兴斗篷cloak技术,你了解吗?
随着互联网技术的飞速发展,网络营销领域也经历了翻天覆地的变革。 从最早的网络横幅广告到如今主流的搜索引擎和社交媒体营销,广告形式变得越来越多样。 其中,搜索引擎广告一直以其精准投放而备受青睐,但近年来,一项名…...
:不变子群的几道例题)
【抽代复习笔记】34-群(二十八):不变子群的几道例题
例1:证明,交换群的任何子群都是不变子群。 证:设(G,o)是交换群,H≤G, 对任意的a∈G,显然都有aH {a o h|h∈H} {h o a|h∈H} Ha。 所以H⊿G。 【注:规范的不变子群符号是一个顶角指向左边…...
Chrome和Firefox如何保护用户的浏览数据
在当今数字化时代,保护用户的浏览数据变得尤为重要。浏览器作为我们日常上网的主要工具,其安全性直接关系到个人信息的保密性。本文将详细介绍Chrome和Firefox这两款主流浏览器如何通过一系列功能来保护用户的浏览数据。(本文由https://chrom…...

CentOS 7镜像下载
新版本系统镜像下载(当前最新是CentOS 7.4版本) CentOS官网 官网地址 http://isoredirect.centos.org/centos/7.4.1708/isos/x86_64/ http://mirror.centos.org/centos/7/isos/ 国内的华为云,超级快:https://mirrors.huaweiclou…...

opencv-windows-cmake-Mingw-w64,编译opencv源码
Windows_MinGW_64_OpenCV在线编译动态库,并使用在C项目: (mingw-w64 cmakegithub actions方案) 修改版opencv在线编译: 加入opencv-contrib库, 一起编译生成动态库,在线编译好的opencv动态库,可以下载使用.验证opencv动态库是否可用的模板项目,测试opencv动态库是否可用的模板…...

Puppeteer点击系统:解锁百度流量点击率提升的解决案例
在数字营销领域,流量和搜索引擎优化(SEO)是提升网站可见性的关键。我开发了一个基于Puppeteer的点击系统,旨在自动化地提升百度流量点击率。本文将介绍这个系统如何通过模拟真实用户行为,优化关键词排名,并…...
Kyber原理解析
Kyber是一种IND-CCA2安全的密钥封装机制。Kyber的安全性基于在模格(MLWE问题)中解决LWE问题的难度。Kyber的构造采⽤两阶段⽅法:⾸先介绍⼀种⽤来加密固定32字节⻓度的消息原⽂的IND-CPA安全性的公钥加密⽅案,我们称之为 CPAPKE&a…...
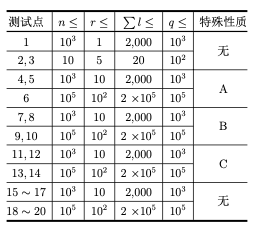
2024 CCF CSP-J/S 2024 第二轮认证 真题试卷
2024年信息学奥赛CSP-J2入门级复赛真题试卷 题目总数:4 总分数:400 编程题 第 1 题 问答题 扑克牌(poker) 【题目描述】 小 P 从同学小 Q 那儿借来一副 n 张牌的扑克牌。 本题中我们不考虑大小王,此时每张牌具有两个属性:花色和…...

Android 无障碍服务常见问题梳理
android 无障碍服务本意是为了帮助盲人操作手机而设计,但是现在也有人利用这个做自动化操作。 本片文章讲述的主要用作自动化方面。 官方文档 关于配置方法和接口列表,参考 无障碍 比较常用的接口: 1. 执行点击操作 2. 触摸屏幕…...

Milvus 与 Faiss:选择合适的向量数据库
向量数据库 Milvus 和 Faiss 都是处理大规模向量数据的工具,尤其适用于需要相似性搜索的场景,比如推荐系统、图像检索和自然语言处理等。但它们各自的设计初衷和功能有所不同,适用于不同的使用场景。下面,我们从性能、功能特性、部…...

2024最全CTF入门指南、CTF夺旗赛及刷题网站(建议收藏!)
文章目录 一、赛事介绍二、竞赛模式三、CTF各大题型简介四、赛题情况分析CTF 工具集合Web | Web 安全🕸 MISC | 杂项❆ 基础工具❆ 解题工具❆ 开源脚本🔑 Crypto | 密码学 💫 Reverse | 逆向基础工具💥 PWN | 二进制 ὄ…...

【论文阅读】ESRGAN+
学习资料 论文题目:进一步改进增强型超分辨率生成对抗网络(ESRGAN : FURTHER IMPROVING ENHANCED SUPER-RESOLUTION GENERATIVE ADVERSARIAL NETWORK)论文地址:2001.08073代码:ncarraz/ESRGANplus: ICASSP …...
北京市首发教育领域人工智能应用指南,力推个性化教育新篇章
近年来,人工智能在全球教育领域的应用呈现蓬勃发展之势,各国都在探索如何将其更好的融入教育体系,在这一背景下,北京市于10月26日发布《北京市教育领域人工智能应用指南》(以下简称《指南》),推…...

【Java并发编程】信号量Semaphore详解
一、简介 Semaphore(信号量):是用来控制同时访问特定资源的线程数量,它通过协调各个线程,以保证合理的使用公共资源。 Semaphore 一般用于流量的控制,特别是公共资源有限的应用场景。例如数据库的连接&am…...
window11使用wsl2安装Ubuntu22.04
目录 1、快速了解wsl2 安装子系统linux流程(B站视频) 2、wsl2常用命令 3、windows与子系统Linux文件访问方法 4、子系统linux使用windows网络代理、网络配置(镜像网络,非NAT) 5、wsl2 Ubuntu miniconda 安装 6、…...
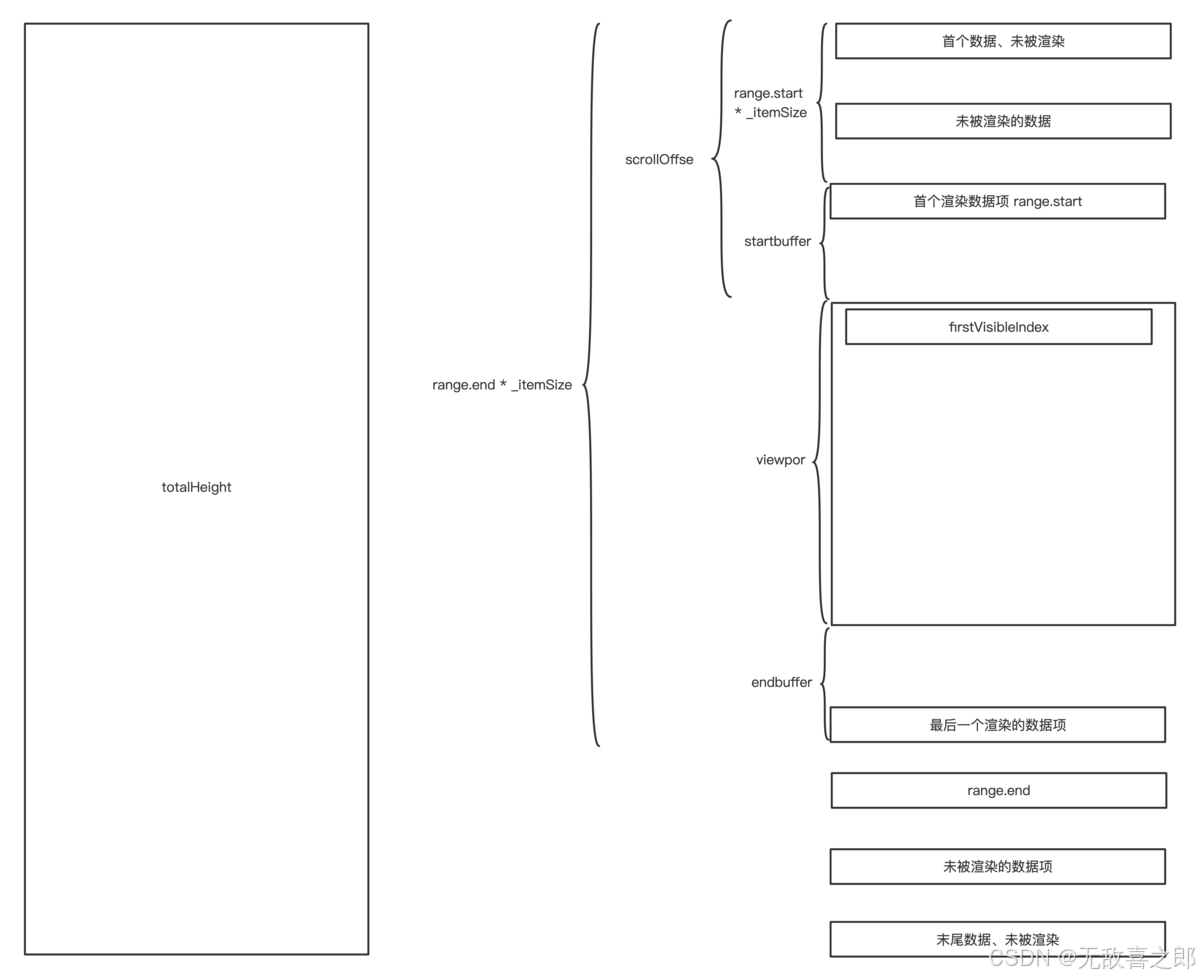
虚拟滚动 - 从基本实现到 Angular CDK
简介 在大数据列表的处理上,虚拟滚动是一种优化性能的有效方式。本篇文章将详细介绍两种常见的虚拟滚动实现方式:使用 transform 属性和 Intersection Observer。重点讲解如何通过 transform 属性实现高效的虚拟滚动,并对比Angular CDK中的实…...
)
Spring WebFlux学习笔记(一)
核心思想 WebFlux主要是异步 例子 参考一个源码: https://blog.csdn.net/qq_43923045/article/details/106309432?spm1001.2014.3001.5506 GetMapping("/delay1")public Mono<RestResult> delayResult() {long l System.currentTimeMillis();…...

富格林:正确追损思维安全交易
富格林指出,对于如何正确追损的这个问题是需要持续付出时间和精力的,发现具备耐心的投资者往往在正确追损的路上更加游刃有余。他们总是可以保持较为平和的心态,不急不躁地分析原因并通过自身掌握的安全应对措施来进行交易。富格林在以下分享…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...
