计算机低能儿从0刷leetcode | 33.搜索旋转排列数组
题目:33. 搜索旋转排序数组
思路:看到时间复杂度要求是O(log N)很容易想到二分查找,普通的二分查找我们已经掌握,本题中的数组可以看作由两个分别升序的数组拼成,在完全升序的部分中进行二分查找是容易的,因此我们每次找到mid后,判断mid左侧为完全升序还是右侧为完全升序,比如,若mid左侧为完全升序,此时如果target的范围在这当中(即nums[i]-nums[mid]中),那么就去左边寻找,否则都去右边。
因此,主要思路为以下几部分:
1、判断哪一侧是完全升序的。nums[l]<nums[mid]则左侧完全升序、否则是右侧。
2、若左侧有序且target在这个范围中,就去左边寻找,否则去右边。
3、若右侧有序且target在这个范围中,就去右边寻找,否则去左边。
4、若找不到则返回-1.
代码:
class Solution {
public:int search(vector<int>& nums, int target) {int len=nums.size();int l=0,r=len-1;while(l<=r){int mid = (l+r)/2;if(target==nums[mid]) return mid;if(nums[l]<=nums[mid]){if(target>=nums[l]&&target<nums[mid]) r=mid-1;else l=mid+1;}else if(target>nums[mid]&&target<=nums[r]) l=1+mid;else r=mid-1; }return -1;}
};补充:
在二分法中,左右指针的移动和循环条件的细微改变都会引起结果的不同。比如循环条件是while(l<r) 还是 while(l<=r),指针移动方式是l=mid,还是l=mid+1。我没有深入研究原理,只是观察并且猜测while(l<=r)与l=mid+1搭配使用是其中一种正确的方式,也许可以死板地记忆以下。
相关文章:

计算机低能儿从0刷leetcode | 33.搜索旋转排列数组
题目:33. 搜索旋转排序数组 思路:看到时间复杂度要求是O(log N)很容易想到二分查找,普通的二分查找我们已经掌握,本题中的数组可以看作由两个分别升序的数组拼成,在完全升序的部分中进行二分查找是容易的,…...
SpringBoot+VUE2完成WebSocket聊天(数据入库)
下载依赖 <!-- websocket --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId></dependency><!-- MybatisPlus --><dependency><groupId>com.ba…...
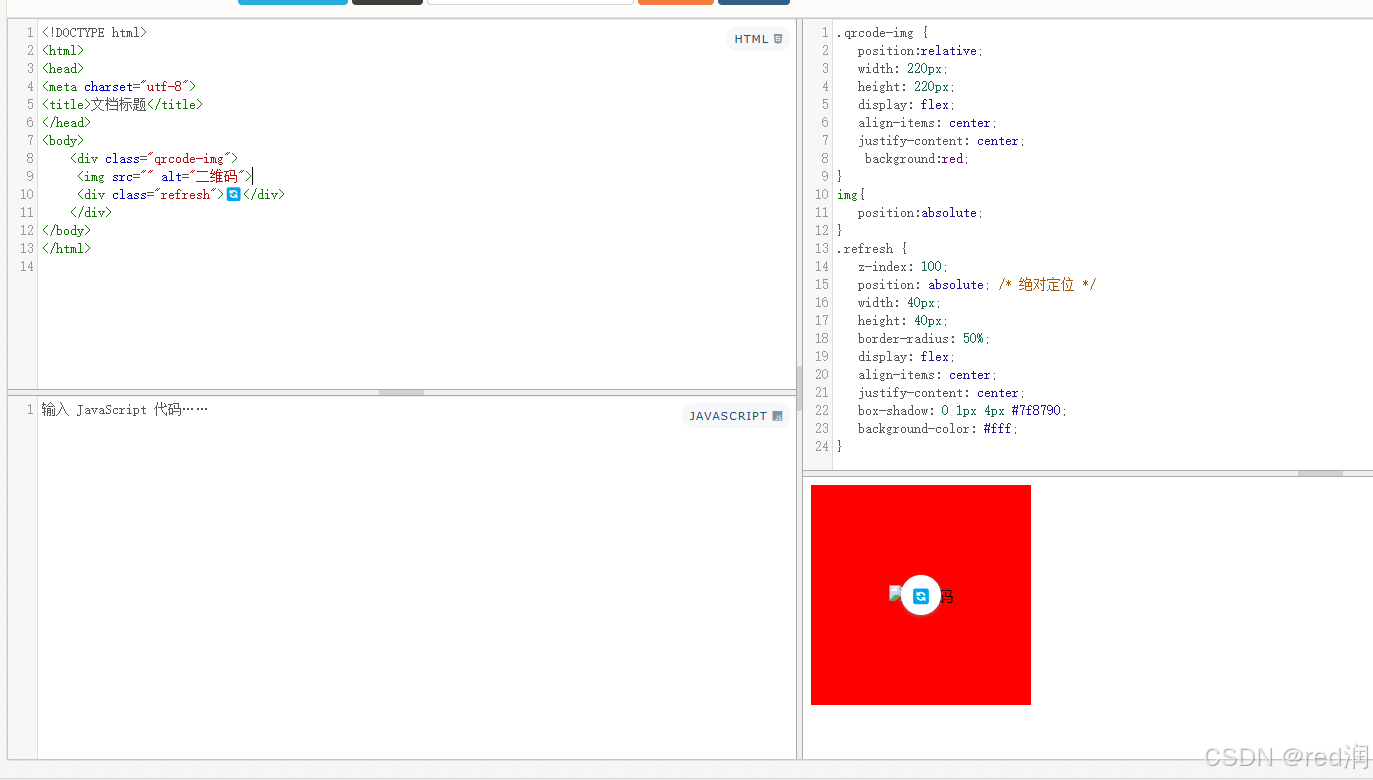
理解 CSS 中的绝对定位与 Flex 布局混用
理解 CSS 中的绝对定位与 Flex 布局混用 在现代网页设计中,CSS 布局技术如 flex 和绝对定位被广泛使用。然而,这两者结合使用时,可能会导致一些意想不到的布局问题。本文将探讨如何正确使用绝对定位元素,避免它们受到 flex 布局的…...

Redis 事务 问题
前言 相关系列 《Redis & 目录》《Redis & 事务 & 源码》《Redis & 事务 & 总结》《Redis & 事务 & 问题》 参考文献 《Redis事务详解》 Redis事务是什么? 标准的事务是指执行时具备原子性/一致性/隔离性/持久性的一系列操作。…...

Cpp学习手册-进阶学习
C标准库和C20新特性 C标准库概览: 核心库组件介绍: 容器: C 标准库提供了多种容器,它们各有特点,适用于不同的应用场景。 std::vector: vector:动态数组,支持快速随机访问。 #in…...

代码随想录-字符串-反转字符串中的单词
题目 题解 法一:纯粹为了做出本题,暴力解 没有技巧全是感情 class Solution {public String reverseWords(String s) {//首先去除首尾空格s s.trim();String[] strs s.split("\\s");StringBuilder sb new StringBuilder();//定义一个公共的字符反转…...
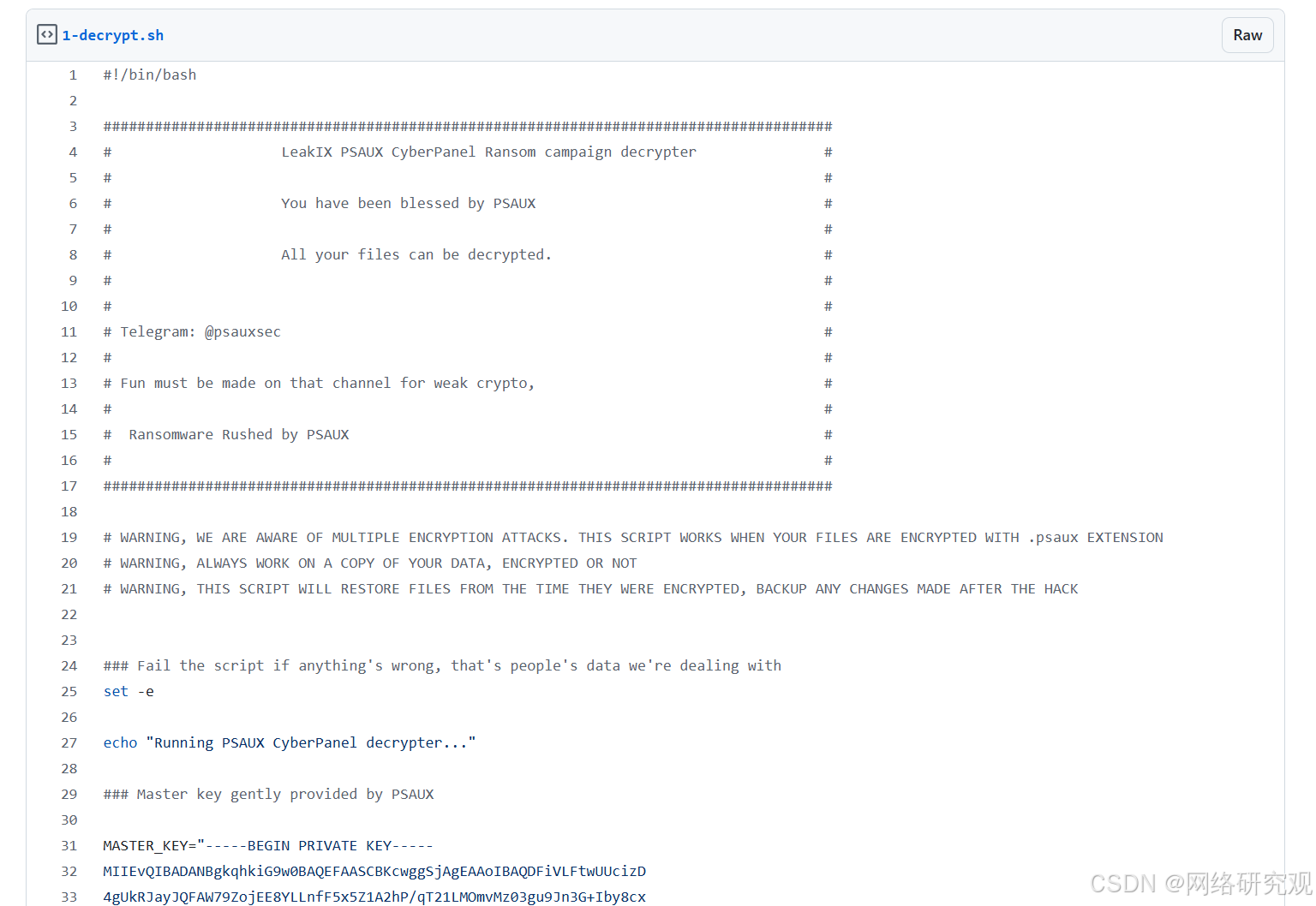
勒索软件通过易受攻击的 CyberPanel 实例攻击网络托管服务器
一个威胁行为者(或可能多个)使用 PSAUX 和其他勒索软件攻击了大约 22,000 个易受攻击的 CyberPanel 实例以及运行该实例的服务器上的加密文件。 PSAUX 赎金记录(来源:LeakIX) CyberPanel 漏洞 CyberPane…...

Open WebUI + openai API / vllm API ,实战部署教程
介绍Open WebUI + Ollama 的使用: https://www.dong-blog.fun/post/1796 介绍vllm 的使用:https://www.dong-blog.fun/post/1781 介绍 Ollama 的使用: https://www.dong-blog.fun/post/1797 本篇博客玩个花的,Open WebUI 本身可以兼容openai 的api, 那来尝试一下。 仅供…...

InsuranceclaimsController
目录 1、 InsuranceclaimsController 1.1、 保险理赔结算 1.2、 生成预约单号 1.3、 保存索赔表 InsuranceclaimsController using QXQPS.Models; using QXQPS.Vo; using System; using System.Collections; using System.Collections.Generic; using System.Li…...
如何成为开源代码库Dify的contributor:解决issue并提交PR
前言 Dify 是一个开源的大语言模型(LLM)应用开发平台,它融合了后端即服务(Backend as Service)和LLMOps的理念,旨在简化和加速生成式AI应用的创建和部署。Dify提供了一个用户友好的界面和一系列强大的工具…...
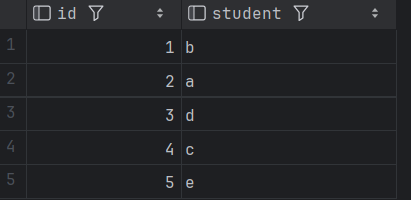
SQL进阶技巧:巧用异或运算解决经典换座位问题
目录 0 问题描述 1 数据准备 2 问题分析 2.1 什么是异或 2.2异或有什么特性? 2.3 异或应用 2.4 本问题采用异或SQL解决方案 3 小结 0 问题描述 表 seat中有2个字段id和student id 是该表的主键(唯一值)列,student表示学生姓名。 该表的每一行都表示学生的姓名和 ID。…...
进行监控)
【MySQL】 运维篇—数据库监控:使用MySQL内置工具(如SHOW命令、INFORMATION_SCHEMA)进行监控
随着应用程序的增长,数据库的性能和稳定性变得至关重要。监控数据库的状态和性能可以帮助数据库管理员(DBA)及时发现问题,进行故障排查,并优化数据库的运行效率。通过监控工具,DBA可以获取实时的性能指标、…...
【温酒笔记】DMA
参考文档:野火STM32F103 1. Direct Memory Access-直接内存访问 DMA控制器独立于内核 是一个单独的外设 DMA1有7个通道DMA2有5个通道DMA有四个等级,非常高,高,中,低四个优先级如果优先等级相同,通道编号越…...

力扣判断字符是否唯一(位运算)
文章目录 给一个数n,判断它的二进制位中第x位是0还是1(从0开始计数)将一个数n的二进制位第X位修改为1(从0开始计数)将一个数n的二进制第x位修改为0(从0开始计数)提取一个数n二进制中最右侧的1去掉一个数n二进制表示中最右侧的1 今天我们通过判断字符是否唯一这个题来了解位运算…...
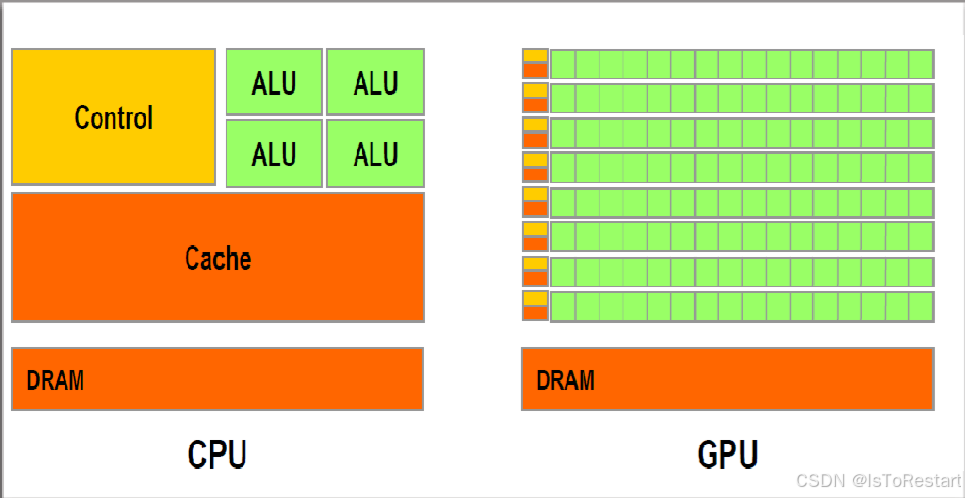
GPU和CPU区别?为什么挖矿、大模型都用GPU?
GPU(图形处理单元)和CPU(中央处理单元)是计算机中两种不同类型的处理器,它们在设计和功能上有很大的区别。 CPU是计算机的大脑,专门用于执行各种通用任务,如操作系统管理、数据处理、多任务处理等。它的架构设计旨在适应多种任务,…...
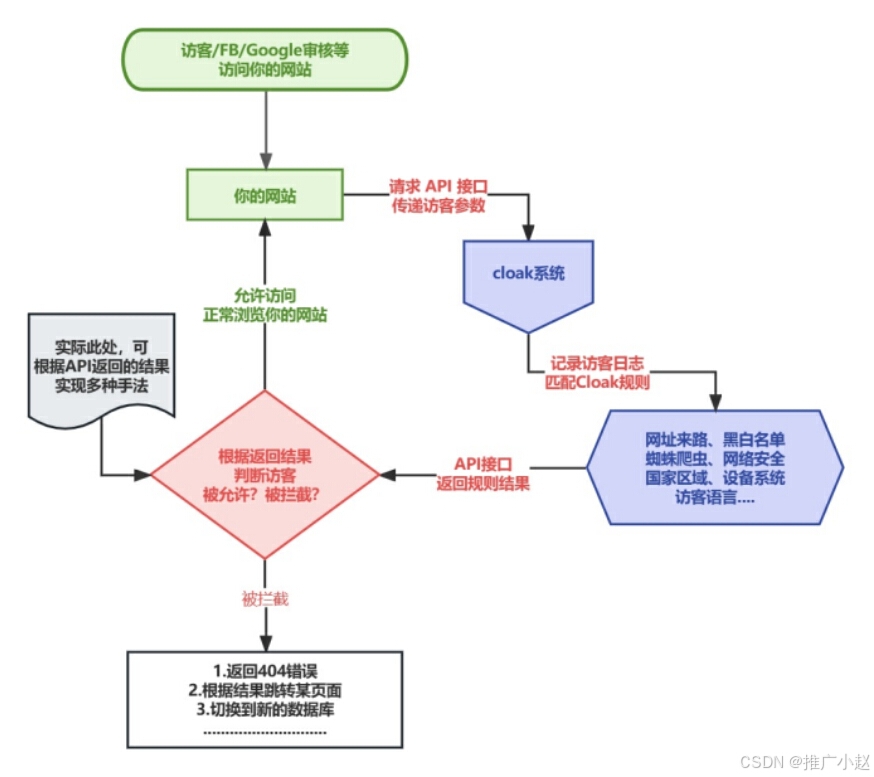
新兴斗篷cloak技术,你了解吗?
随着互联网技术的飞速发展,网络营销领域也经历了翻天覆地的变革。 从最早的网络横幅广告到如今主流的搜索引擎和社交媒体营销,广告形式变得越来越多样。 其中,搜索引擎广告一直以其精准投放而备受青睐,但近年来,一项名…...
:不变子群的几道例题)
【抽代复习笔记】34-群(二十八):不变子群的几道例题
例1:证明,交换群的任何子群都是不变子群。 证:设(G,o)是交换群,H≤G, 对任意的a∈G,显然都有aH {a o h|h∈H} {h o a|h∈H} Ha。 所以H⊿G。 【注:规范的不变子群符号是一个顶角指向左边…...
Chrome和Firefox如何保护用户的浏览数据
在当今数字化时代,保护用户的浏览数据变得尤为重要。浏览器作为我们日常上网的主要工具,其安全性直接关系到个人信息的保密性。本文将详细介绍Chrome和Firefox这两款主流浏览器如何通过一系列功能来保护用户的浏览数据。(本文由https://chrom…...

CentOS 7镜像下载
新版本系统镜像下载(当前最新是CentOS 7.4版本) CentOS官网 官网地址 http://isoredirect.centos.org/centos/7.4.1708/isos/x86_64/ http://mirror.centos.org/centos/7/isos/ 国内的华为云,超级快:https://mirrors.huaweiclou…...

opencv-windows-cmake-Mingw-w64,编译opencv源码
Windows_MinGW_64_OpenCV在线编译动态库,并使用在C项目: (mingw-w64 cmakegithub actions方案) 修改版opencv在线编译: 加入opencv-contrib库, 一起编译生成动态库,在线编译好的opencv动态库,可以下载使用.验证opencv动态库是否可用的模板项目,测试opencv动态库是否可用的模板…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
