力扣题目解析--整数反转
题目
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
输入:x = 123 输出:321
示例 2:
输入:x = -123 输出:-321
示例 3:
输入:x = 120 输出:21
示例 4:
输入:x = 0 输出:0
提示:
-231 <= x <= 231 - 1
代码展示
class Solution {
public:int reverse(int x) {string ret=to_string(x);int length=ret.size();string str="";if(ret[0]=='-'){str+="-";}for(int i=length-1;i>=0;i--){if (ret[i] != '-') {str += ret[i];}}try {int num = std::stoi(str);return num;} catch (const std::out_of_range& e) {// 如果转换失败(溢出),返回0return 0;}}
};
逐行解析
-
类定义:
class Solution { public:定义一个名为
Solution的类,并声明一个公共成员函数reverse。 -
函数定义:
int reverse(int x) {定义一个公共成员函数
reverse,接受一个整数参数x并返回一个整数。 -
将整数转换为字符串:
string ret = to_string(x);使用
to_string函数将整数x转换为字符串ret。 -
获取字符串的长度:
int length = ret.size();获取字符串
ret的长度,并将其存储在length变量中。 -
创建一个空字符串来存储反转后的结果:
string str = "";初始化一个空字符串
str,用于存储反转后的结果。 -
处理负号:
if (ret[0] == '-') {str += "-"; }检查字符串
ret的第一个字符是否为负号。如果是,将负号添加到结果字符串str中。 -
从后向前遍历字符串,将字符添加到结果字符串中
for (int i = length - 1; i >= 0; i--) {if (ret[i] != '-') {str += ret[i];} }- 使用一个
for循环从字符串ret的最后一个字符开始,向前遍历。 - 在每次迭代中,检查当前字符是否为负号。如果不是,将其添加到结果字符串
str中。
- 使用一个
-
尝试将字符串转换为整数:
try {int num = std::stoi(str);return num; } catch (const std::out_of_range& e) {// 如果转换失败(溢出),返回 0return 0; }- 使用
try块尝试将结果字符串str转换为整数num。 - 如果转换成功,返回
num。 - 如果转换失败(例如,溢出),捕获
std::out_of_range异常并返回0。
- 使用
总结
- 字符串转换:使用
to_string将整数转换为字符串。 - 处理负号:在遍历字符串时,先处理负号,确保负号被正确添加到结果字符串中。
- 字符串反转:从后向前遍历字符串,将字符添加到结果字符串中。
- 整数转换:使用
std::stoi将结果字符串转换为整数,并捕获可能的异常。
这个题相比于回文数。最困难的一点其实在于溢出这个异常处理
相关文章:

力扣题目解析--整数反转
题目 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。 假设环境不允许存储 64 位整数(有符号或无符号)。 示例 1:…...

净水前置需要安装吗?
业主问净水前置需不需要安装?是必须安装吗?这个问题其实很难回答,如果说非要安装,有可能客户会感觉我们在这上面要挣钱, 有很多业主没有安装家里用水也没有问题,如果说不需要安装,现在…...

在深度学习研究方向有哪些创新点
以下是深度学习研究方向的一些创新点: 一、模型架构创新 Transformer架构及其扩展 自注意力机制 Transformer架构摒弃了传统的卷积神经网络(CNN)和循环神经网络(RNN)中的卷积和循环结构,引入了自注意力机…...

YOLOv11改进策略【卷积层】| 2024最新轻量级自适应提取模块 LAE 即插即用 保留局部信息和全局信息
一、本文介绍 本文记录的是利用轻量级自适应提取模块(LAE)模块优化YOLOv11的目标检测网络模型。LAE (Lightweight Adaptive Extraction) 在减少参数和计算成本的同时,能够提取更丰富语义信息的特征,克服了传统卷积方法难以捕捉全局信息的问题,并能更好地提取ROI特征。本文将…...

工作转型与个人突破提升:如何在社会浪潮中激流勇进
文章目录 一、写在前面二、技术人的迷茫三、做好项目经理其实很难四、从纯技术者转型为管理者面临的事五、最重要的技能【重磅推荐!免费简单内网穿透神器!支持linuxwindows】 一、写在前面 近期工作变动,虽然说对于开发者而言,工…...

mongodb:增删改查和特殊查询符号手册
前言 最近考虑开发游戏,网上推荐使用非关系数据库mongodb,因此浅尝了一番,并将一些语句和符号记录在这里。 相对于mysql、oracle这些关系型数据库,基于json文档的mongodb在很多地方都与之大不相同(可以类比为TCP握手连…...

你的Mac book多久没有清洁键盘屏幕了,Mac清洁好帮手来了
你的Mac book键盘使用时间长了不会打油吗,你的屏幕使用久了不会沾灰吗,那你还不清洁一下 你不清洁的原因,是怕清洁键盘误触发吗,还是怕屏幕擦不干净白擦,还是觉得每次都要睡眠或关机再清洁很麻烦 Cleaner是Mac的清洁…...

ANA基因组数据库(ANAgdb)
ANA进化阶由早期发育的被子植物谱系组成,包括无油樟目(Amborellales)、睡莲目(Nymphaeales)和木兰藤目(Austrobaileyales),在进化上具有重要地位。 ANA基因组数据库(ANA…...

leetcode 704 二分查找
704. 二分查找 已解答 简单 相关标签 相关企业 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 示例 1: 输入: nu…...
)
Vue学习笔记(十一)
一. Promise 1. 异步 异步:则是将耗时很长的A交付的工作交给系统之后,就去继续做B交付的工作,等到系统完成了前面的工作之后,再通过回调或者事件,继续做A剩下的工作。AB工作的完成顺序,和交付他们的时间顺…...

ABAP进阶学习1:动态内表1-通过系统表LVC_T_FCAT类型定义内表
动态内表1-通过系统表LVC_T_FCAT类型定义内表 如果对你有帮助,点个关注收藏吧~ 做BW做久了,突然对abap有了探索欲,开始进一步学习abap了,以后这个系列会逐步更新,欢迎小伙伴点个关注一起学习,我学习的方法…...

【Vispy库】一个用于高性能交互式2D/3D数据可视化库 Python库
Vispy库 1、你好,Vispy!2、安装Vispy,轻松上手3、案例一:绘制简单的2D图形4、案例二:3D图形的绘制5、案例三:大规模数据的可视化6、结语 1、你好,Vispy! Vispy是一个用于Python的高…...

为什么 C 语言数组是从 0 开始计数的?
C 语言等大多数编程语言的数组从 0 开始而不从 1 开始,有两个原因: 第一:地址计算更方便 C 语言从 0 开始的话,array[i] 的地址就正好是: (array i) 如果是从 1 开始的话,就是 (array i - 1) 多一次计…...

matlab线性度计算程序
matlab线性度计算程序 环境 matlab2023a ads2020 原理 其中f(v)是曲线,fmax是f(v)的最大值,fmin是f(v)的最小值,vmax为fmax对应v值,vmin为fmin对应v值。 L∆fmax/(fmax-fmin) (1) ∆fmaxmax[f(v)-[fmin-K*(v-vmin)]] (2) K(…...
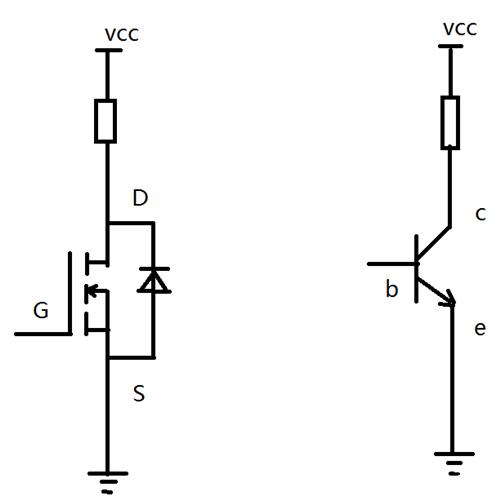
为什么NMOS管比PMOS管更受欢迎?
NMOS在实际应用中为何比PMOS要更受欢迎。本文将从导电沟道、电子迁移率和器件速度等多个方面来展开讲解。 首先是在性能方面考虑: 与NMOS管驱动能力相同的一个PMOS管,其器件面积可能是NMOS管的2~3倍,然而器件面积会影响导通电阻…...

【论文复现】短期电力负荷
作者主页: 七七的个人主页 文章收录专栏: 论文复现 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖💖 短期电力负荷 论文发表问题背景一. 基本问题二. 本论文发现的问题 对于论文发现问题的解决方案:复现…...

pytest脚本常用的执行命令
pytest脚本常用的执行命令 一、一般执行的脚本,执行.py文件整个脚本二、执行.py文件脚本中的一个模块三、执行脚本,执行.py文件整个脚本,或则一个模块,查看对应的日志信息3.1.py文件执行allure的脚本3.2去dos框下去执行对应的脚本…...

OpenCv入门
一.OpenCv简介 1 图像的起源 1.1图像是什么? 图:是物体反射或透射光的分布 像:是人的视觉系统所接受的图在人脑中所形版的印象或认识 1.2模拟图像和数字图像 模拟图像:连续存储的图像 数字图像:分级存储的图像 2 数字…...
)
超详细的flex教程(面试必考)
引言 为什么存在? Flex 布局的出现是为了解决传统 CSS 布局方式(如浮动布局、定位布局等)在处理复杂布局时的诸多限制和不便。 优势 1. 简化布局 Flex 布局的语法简洁明了,代码更易读。 2. 强大的对齐能力 提供丰富的对齐属…...

C++的输入与输出
一.格式和注意要点 1. #include<iostream>; using namespace std; 标准库定义了4个IO对象,IO(输入输出),以下: cin是一个istream流对象,现在理解为标准输入即可。cout是一个ostream流对象,理解为标准输出即可。…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
