Cpp二叉搜索树的讲解与实现(21)
文章目录
- 前言
- 一、二叉搜索树的概念
- 定义
- 特点
- 二、二叉树的实现
- 基本框架
- 查找
- 插入
- 删除
- 当只有0 ~ 1个孩子的时候
- 当有2个孩子的时候
- 三、二叉树的应用
- K模型
- KV模型
- 四、二叉树的性能分析
- 总结
前言
这是全新的一个篇章呢,二叉搜索树是我们接下来学习set、map的前提
迈过它吧,关关难过关关过!
正文开始!
一、二叉搜索树的概念
定义
二叉搜索树(Binary search tree)是基于二叉树的一种改进版本。因为 普通二叉树没有实际价值,无法进行插入、删除等操作(无意义),但二叉搜索树就不一样了,二叉搜索树对于数据的存储有严格要求:左节点比根小,右节点比根大
因此 二叉搜索树 的查找效率极高,具有一定的实际价值
所以将数据存入 二叉搜索树 中进行查找时,理想情况下只需要花费 logN 的时间(二分思想)
这就是 二叉搜索树 名字的由来,搜索(查找)速度很快
特点
二叉树的基本特点:左比根小,右比根大
- 若某个节点的 左 节点不为空,则 左 节点的值一定比当前节点的值 小,且其 左 子树的所有节点都比它 小
- 若某个节点的 右 节点不为空,则 右 节点的值一定比当前节点的值 大,且其 右 子树的所有节点都比它 大
- 二叉搜索树的每一个节点的 根、左 、右 都满足基本特点
另外,中序遍历的结果为升序
二、二叉树的实现
二叉搜索树的源代码
基本框架
跟普通的二叉树一样,二叉搜索树也需要节点类,同时将节点指针作为二叉搜索树的成员变量
template <class K>
struct BSTNode
{K _key;BSTNode<K>* _left;BSTNode<K>* _right;BSTNode(const K& key = K()):_key(key),_left(nullptr),_right(nullptr){}};template <class K>
class BSTree
{typedef BSTNode<K> Node;
public:BSTree():_root(nullptr){}private:Node* _root;
};
查找
得益于二叉搜索树的特性,我们可以比较插入数字和当前节点的值,当比当前节点大的时候的时候往右走,反之则往左,若 cur 为空,那么返回 false ,若找到,则返回 true

bool Find(const K& key)
{Node* cur = _root;while (cur) {if (key > cur->_key) cur = cur->_right;else if (key < cur->_key) cur = cur->_left;else return true;}return false;
}
插入
插入其实过程和查找差不多,只不过如果中途找到了就返回 false 表示二叉搜索树中已经有该数字,如果成功走到空了就开始插入

只不过我们需要注意,当搜索树为空树的时候,我们必须新建立一个节点,将指针赋给这个根节点,另外,我们需要申请一个指针变量 parent 来记录父节点,方便后续链接
bool Insert(const K& key)
{// 如果为空树,则直接建立一个节点// 将其地址存放在_root上if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;// 一直循环到cur为空while (cur) {if (key > cur->_key) {parent = cur;cur = cur->_right;}else if (key < cur->_key) {parent = cur;cur = cur->_left;}else {// 如果中途发现BS树已有key,则插入失败// BS树中没有重复元素,依据定义return false;}}// 此时建立一个节点,将其地址赋值给curcur = new Node(key);// 此时需要根据值的大小来判断parent左链还是右链if (key > parent->_key)parent->_right = cur;else parent->_left = cur;return true;
}
删除
删除可就复杂了,要考虑很多情况!
我们发现如果我们要删除一个节点,并且在二叉搜索树中已经确定找到了该节点,可能有三种情况:
- 该节点没有孩子,即要删除的是叶子节点
- 该节点只有一个孩子,可能是左孩子为空,也有可能是有孩子为空
- 该节点有两个孩子,这种情况比较复杂,要考虑比较复杂的情况
当只有0 ~ 1个孩子的时候
我们先来看第二种情况,当找到要删除的节点且该节点只有一个孩子后,此时显然父节点链上当前节点的子节点就可以了,这样不会破坏二叉搜索树的结构
二叉搜索树的右子树的值一定大于该节点的值,同样的,左子树的值一定小于该节点的值
于是,我们就想着再销毁当前节点之前,先判断是父节点的左边链接还是右边链接,这很简单,我们检查一下 parent 左右指针哪个指向 cur 就行,同时,我们也要思考一下子节点与 cur 的链接关系,很简单,这也是直接判断一下就可以
其实,这种方法囊括了第一第二种情况,你可以思考一下为什么
// 如果左孩子为空
// 这时候就要parent就要链到cur的右边去
if (cur->_left == nullptr) {if (parent->_left == cur)parent->_left = cur->_right;else parent->_right = cur->_right;// 删除delete cur;cur = nullptr;return true;
}// 如果右孩子为空
// 这时候就要parent就要链到cur的左边去
else if (cur->_right == nullptr) {if (parent->_left == cur)parent->_left = cur->_left;else parent->_right = cur->_left;// 删除delete cur;cur = nullptr;return true;
}
右子树为空
左子树为空
当有2个孩子的时候

当左右孩子节点都不为空的时候,我们也要想想,万一把 cur 给删掉了,要换那一个替上来?
关于这个问题,我们还是要把握二叉搜索树的一个核心特性,就是左子树所有节点的值一定比根节点小,右子树所有节点的值一定比根节点大
那么只要将左子树最大的值和右子树最小的值找到,此时我们又要想,将两个其中之一的值替代父节点的值即可,然后再销毁节点,那么这样会不会破坏二叉树的结构呢?
显然不会,只要能正确销毁并正确链接,那么就没关系,在这里我们选择找到右子树的最小值,这很简单,因为一个二叉搜索树的最小值就是最左边那个,那么我们同样用 rightMin 标记右子树的最小节点 ,用 rightMinP 标记其父节点,又为了防止 rightMinP 进不去循环,我们给 rightMinP 赋值 cur
Node* rightMinP = cur;
Node* rightMin = cur->_right;// 找到右子树的最小节点
while (rightMin->_left) {rightMinP = rightMin;rightMin = rightMin->_left;
}// 替代,这时候转换成就要删除rightMin这个节点了
// 这个时候就需要有它的父亲
cur->_key = rightMin->_key;// 因为rightMin必然是最左节点
// 所以rightMinP必然是链接rightMin的右孩子
// 同时rightMinP是左链还是右链这不确定,需要判断一下
if (rightMinP->_left == rightMin)rightMinP->_left = rightMin->_right;
else rightMinP->_right = rightMin->_right;delete rightMin;
rightMin = nullptr;return true;
但是但是!!我们发现写到这里后,当删到最后只剩几个节点之后,报错了!
我们再回看代码,发现我们的逻辑是先找到删除节点,再用父亲节点去链接当前节点的子节点,关键是,有没有可能一开始我们就找到了要删除的节点,父亲节点没进循环,也就是说,没有父亲节点,这很不好,针对这种情况,我们就要移动根节点
if (parent == nullptr) {_root = _root->_right;delete cur;cur = nullptr;return true;
}
三、二叉树的应用
K模型
K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
我们上述代码实现的也就是这种
举个例子,给一个单词word,判断该单词是否拼写正确,具体方式如下:
- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误
KV模型
每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对
KV模型也就是在K模型的基础上加上value的值,请试试吧!
四、二叉树的性能分析
如果我问你二叉搜索树的查找时间复杂度为多少,你可能会不假思索的回答出是O(logN),但是,假如我给一个递减数列呢,是不是就退化成单支树了?
所以理想状态下是O(logN),最坏情况下是O(N)
总结
看了性能分析,你可能会想怎么让二叉树的性能达到最优?不急,AVL树和红黑树已经在路上了!~
相关文章:

Cpp二叉搜索树的讲解与实现(21)
文章目录 前言一、二叉搜索树的概念定义特点 二、二叉树的实现基本框架查找插入删除当只有0 ~ 1个孩子的时候当有2个孩子的时候 三、二叉树的应用K模型KV模型 四、二叉树的性能分析总结 前言 这是全新的一个篇章呢,二叉搜索树是我们接下来学习set、map的前提 迈过它…...

微服务设计模式 — 补偿事务模式(Compensating Transaction Pattern)
微服务设计模式 — 补偿事务模式(Compensating Transaction Pattern) 定义 在云计算和分布式系统中,管理跨多个微服务或组件的事务一致性是一项极具挑战性的任务,补偿事务模式Compensating Transaction Pattern)是一种…...
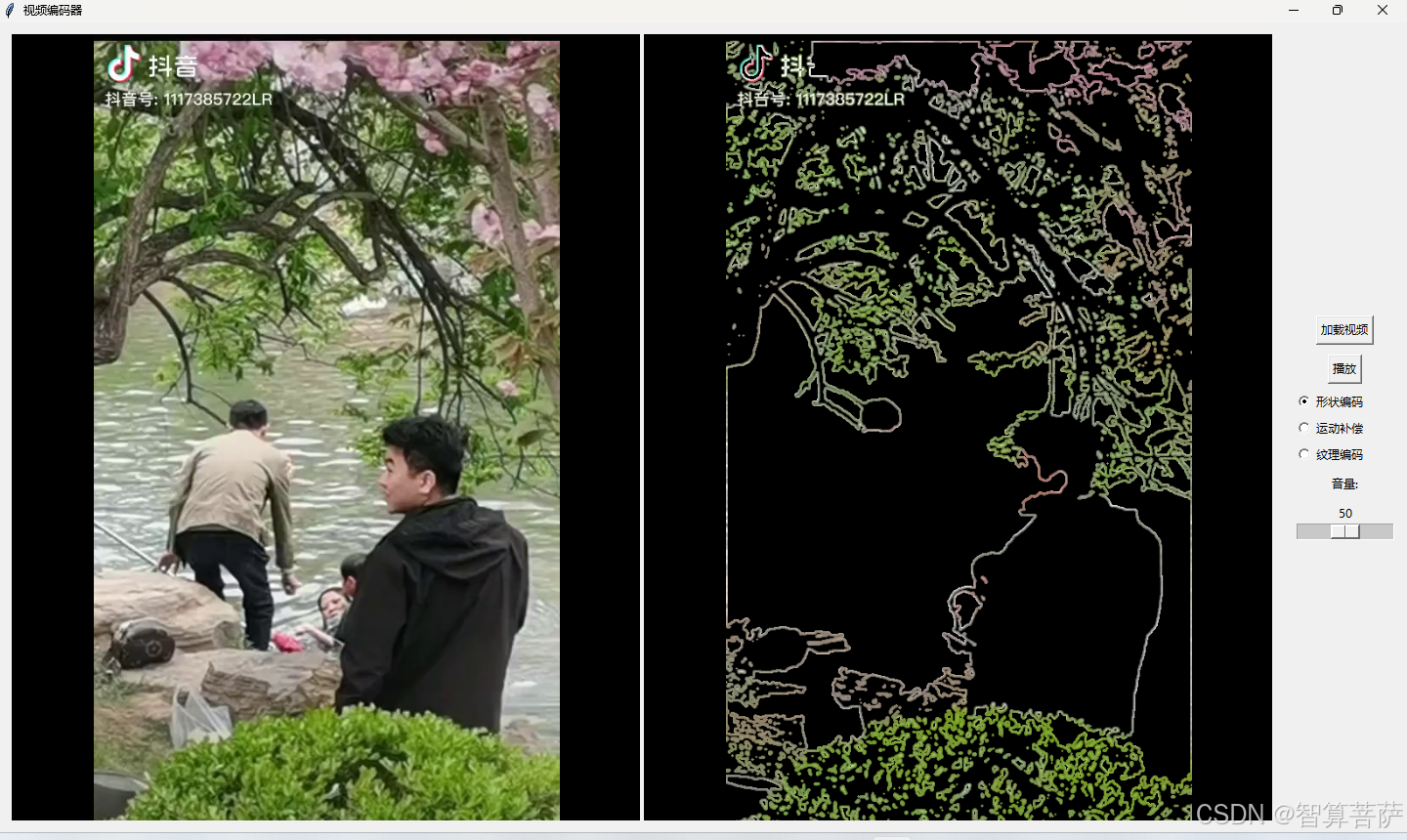
20 实战:形状编码、运动补偿和纹理编码的实现(基于python)
在当今多媒体时代,视频处理与编码已经成为各个领域中不可或缺的一部分。无论是视频编辑、流媒体传输,还是计算机视觉应用,视频编码技术都扮演着关键角色。本文将详细解析一个基于Python的图形用户界面(GUI)视频编码器。通过对代码的逐行讲解、功能分析以及参数调节方法的探…...

区块链-C++挖矿软件XMRIG源码分析
C++挖矿软件源码分析 3rdpartybackendgrgon2Obfusheader.hmain 程序 xmrig.cppxmrig命名空间process类Entry::IdApp类CoreControllerbasetoolkernelinterfacesDonateStrategy.cppdonate.h/2/dmiCmake 跨平台的自动化构建系统CMakeLists.txt.cmake 13个引入算力哈希率 HashrateE…...

C语言指针的介绍
零.导言 在日常生活中,我们常常在外出时居住酒店,细心的你一定能发现酒店不同的房间上有着不同的门牌号,上面写着像308,512之类的数字。当你定了酒店之后,你就会拿到一个写有门牌号的钥匙,凭着钥匙就能进入…...

八大排序算法——堆排序
目录 前言 一、向上调整算法建堆 二、向下调整算法建堆 三、堆排序 前言 堆排序是基于堆结构的一种排序思想,因此要为一个乱序的数组进行排序的前提是数组必须要是一个堆,所以要先对数组进行建堆操作 一、向上调整算法建堆 时间复杂度:O…...
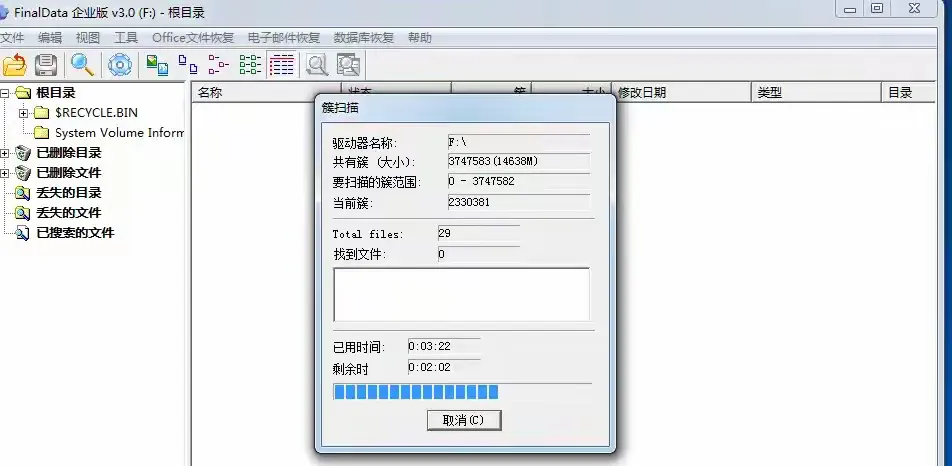
U盘文件不翼而飞?这些数据恢复工具帮你找回!
U盘因其便携性是我们日常工作和生活中不可或缺的工具。不过有时候它也会出点小状况。如果你U盘里的数据突然不见了,不要着急,可以先试试这几款数据恢复工具! 福昕数据恢复 直达链接:www.pdf365.cn/foxit-restore/ 操作教程&…...

在Java中 try catch 会影响性能吗?
1、在Java中,异常处理确实会对性能产生影响,但在正常执行的代码路径中,即没有发生异常的情况下,try-catch块的性能影响是微不足道的 2、但是,如果出现异常被抛出时,Java虚拟机需要执行一些额外的操作来处理…...

吞吐量最高飙升20倍!破解强化学习训练部署难题
**强化学习(RL)对大模型复杂推理能力提升有关键作用,然而,RL 复杂的计算流程以及现有系统局限性,也给训练和部署带来了挑战。近日,字节跳动豆包大模型团队与香港大学联合提出 HybridFlow(开源项…...

redis的数据过期策略
Redis对数据设置了数据的有效时间,数据过期之后,就需要将数据从内存中删除掉.可以按照不同的规则进行删除,这种删除规则就被称之为数据的删除策略(数据过期策略),而这种策略有两种:惰性删除和定期删除 惰性删除:设置key过期时间后,我们不去管它,当需要该key时,我们在检查其是否…...

三周精通FastAPI:27 使用使用SQLModel操作SQL (关系型) 数据库
官网文档:https://fastapi.tiangolo.com/zh/tutorial/sql-databases/ SQL (关系型) 数据库 FastAPI不需要你使用SQL(关系型)数据库。 但是您可以使用任何您想要的关系型数据库。 这里我们将看到一个使用SQLModel的示例。 SQLModel是在SQLAlchemy和Pydantic的基础…...
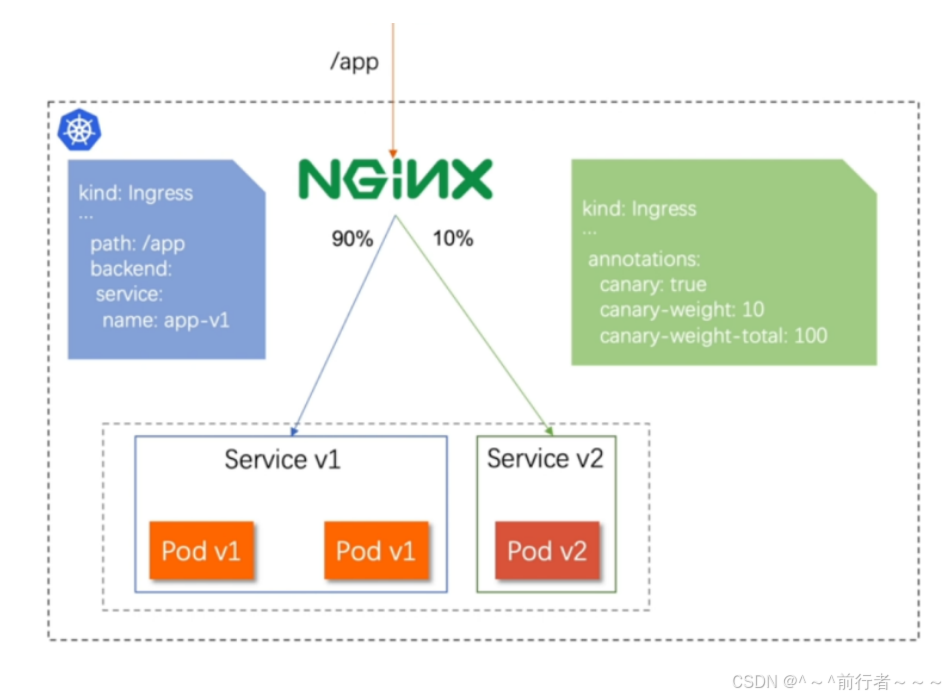
Kubernetes金丝雀发布
华子目录 Canary金丝雀发布什么是金丝雀发布Canary发布方式基于header(http包头)灰度发布基于权重的金丝雀发布 Canary金丝雀发布 什么是金丝雀发布 金丝雀发布也称为灰度发布,是一种软件发布策略主要目的是在将新版本的软件全面推广到生产环…...

树形DP讲解
文章目录 树形DP讲解一、引言二、树形DP基础1、树的定义2、树形DP的基本思想3、代码示例:子树大小 三、经典例题解析1、树的平衡点1.1、代码示例 2、没有上司的舞会(树的最大独立集)2.1、代码示例 四、总结 树形DP讲解 一、引言 树形动态规…...

容器:如何调试容器
调试容器,主要是指的调试Dockerfile,调试Dockerfile中的各个命令的执行,大小等 1、docker history查看构建过程和所有的中间层 2、docker run rm -it -u root XXX sh,通过临时容器的方式启动,可以调试中间层文件 3、do…...

用图说明 CPU、MCU、MPU、SoC 的区别
CPU CPU 负责执行构成计算机程序的指令,执行这些指令所指定的算术、逻辑、控制和输入/输出(I/O)操作。 MCU (microcontroller unit) 不同的 MCU 架构如下,注意这里的 MPU 表示 memory protection unit MPU (microprocessor un…...

牛客周赛 Round 65
文章目录 超市思路:Solved: 雨幕思路:Solved: 闺蜜思路:Solved: 医生思路:Solved: 降温(easy)思路:Solved: F-降温(hard&a…...

超级经典的79个软件测试面试题(内含答案)
1、软件的生命周期(prdctrm) 计划阶段(planning)-〉需求分析(requirement)-〉设计阶段(design)-〉编码(coding)->测试(testing)->运行与维护(running maintrnacne) 测试用例 用例编号 测试项目 测试标题 重要级别 预置条件 输入数据 执行步骤 预期结果 2、问…...

【Mac】安装 F5-TTS
1、下载项目 项目地址:【GitHub】 SWivid F5-TTS 2、创建并激活 Python 虚拟环境 # 创建 Python 虚拟环境 userMac F5-TTS-main % python3 -m venv f5-tts# 激活进入 Python 虚拟环境 userMac F5-TTS-main % source f5-tts/bin/activate (f5-tts) userrMac F5-TT…...

Leaflet查询矢量瓦片偏移的问题
1、问题现象 使用Leaflet绘制工具查询出来的结果有偏移 2、问题排查 1)Leaflet中latLngToContainerPoint和latLngToLayerPoint的区别 2)使用Leaflet查询需要使用像素坐标 3)经排查发现,container获取的坐标是地图容器坐标&…...

存储引擎技术进化
B-tree 目前支撑着数据库产业的半壁江山。 50 年来不变而且人们还没有改变它的意向 鉴定一个算法的优劣,有一个学派叫 IO复杂度分析 ,简单推演真假便知。 下面就用此法分析下 B-tree(traditional b-tree) 的 IO 复杂度,对读、写 IO 一目了…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...


