八大排序算法——堆排序
目录
前言
一、向上调整算法建堆
二、向下调整算法建堆
三、堆排序
前言
堆排序是基于堆结构的一种排序思想,因此要为一个乱序的数组进行排序的前提是数组必须要是一个堆,所以要先对数组进行建堆操作
一、向上调整算法建堆
时间复杂度:O( n*logn )
由于向上调整算法建堆的时间复杂度的证明太过晦涩难懂,还要涉及数学中的错位相减法,所以这里就不证明了,感兴趣的可以自己去了解一下
这里只需要知道向上调整算法建堆的时间复杂度为 O( n*logn )
//交换两个数的位置
void sweap(int* num1, int* num2)
{int tmp = *num1;*num1 = *num2;*num2 = tmp;
}
//向上调整算法(大根堆)
void AdjustUp(int* arr, int pos)
{//当前调整的位置不能是堆顶if (pos == 0){return;}//寻找双亲节点int parents = (pos - 1) / 2;//当前位置与双亲节点进行比较//如果当前位置的数大于双亲节点,就进行交换,并且继续向上调整//如果当前位置的数小于双亲节点,表示堆已经构建好了if (arr[parents] < arr[pos]){//交换两个数位置sweap(&arr[parents], &arr[pos]);//继续向上调整AdjustUp(arr, parents);}
}
int main()
{//给定一个乱序数组int arr[] = { 8,3,2,6,7,1,4,9,5 };//计算数组元素个数int size = sizeof(arr) / sizeof(arr[0]);//向上调整算法建堆//从前往后依次调整建堆//先让节点之前的数为堆,然后整体为堆for (int i = 0; i < size; i++){AdjustUp(arr, i);}return 0;
}
二、向下调整算法建堆
时间复杂度:O( n )
由于向下调整算法建堆的时间复杂度的证明太过晦涩难懂,还要涉及数学中的错位相减法,所以这里就不证明了,感兴趣的可以自己去了解一下
这里只需要知道向下调整算法建堆的时间复杂度为 O( n )
//交换两个数的位置
void sweap(int* num1, int* num2)
{int tmp = *num1;*num1 = *num2;*num2 = tmp;
}
//向下调整算法(大根堆)
void AdjustDown(int* arr, int size, int pos)
{//左孩子位置int child = pos * 2 + 1;//向下调整算法,直到左孩子位置大于数组个数if (child < size){//选出左右孩子中最大的那个孩子if (child + 1 < size && arr[child] < arr[child + 1]){child++;}//与当前位置进行比较//如果左右孩子中最大数大于当前位置的数,就进行交换,并且继续向下调整//如果左右孩子中最大数小于当前位置的数,表示堆已经调整好了if (arr[child] > arr[pos]){//交换两个数的位置sweap(&arr[pos], &arr[child]);//继续向下调整AdjustDown(arr, size, child);}}
}
int main()
{//给定一个乱序数组int arr[] = { 8,3,2,6,7,1,4,9,5 };//计算数组元素个数int size = sizeof(arr) / sizeof(arr[0]);//向上调整算法建堆//从最后一个叶子节点父节点往前依次调整建堆//先让节点的左右子树为堆,然后整体为堆int pos = (size - 1) / 2;//最后一个叶子节点父节点for (int i = pos; i >= 0; i--){AdjustDown(arr, size, i);}return 0;
}
三、堆排序
时间复杂度:O( n*logn )
在进行建堆操作时我们可以选择向上调整算法和向下调整算法,但是由于向下调整算法的时间复杂度要优于向上调整算法,因此更推荐使用向下调整算法建堆
建堆的时间复杂度为O( n ),每次调整的堆结构的时间复杂度为O( logn ) ,因此整体时间复杂度为O( n*logn )
堆排序的过程大致如下:
- 将待排序的数组构造成一个大顶堆(或小顶堆,根据需要)。此时,整个数组的最大值(或最小值)就是堆结构的顶端
- 将顶端的数与末尾的数交换。此时,末尾的数为最大值(或最小值),剩余待排序数组个数为n-1
- 将剩余的n-1个数再构造成大顶堆(或小顶堆),再将顶端数与n-1位置的数交换。如此反复执行,便能得到有序数组
【注意】
- 排升序要建大堆
- 排降序要建小堆
整体代码实现
//交换两个数的位置
void sweap(int* num1, int* num2)
{int tmp = *num1;*num1 = *num2;*num2 = tmp;
}//向下调整算法(大根堆)
void AdjustDown(int* arr, int size, int pos)
{//左孩子位置int child = pos * 2 + 1;//向下调整算法,直到左孩子位置大于数组个数if (child < size){//选出左右孩子中最大的那个孩子if (child + 1 < size && arr[child] < arr[child + 1]){child++;}//与当前位置进行比较//如果左右孩子中最大数大于当前位置的数,就进行交换,并且继续向下调整//如果左右孩子中最大数小于当前位置的数,表示堆已经调整好了if (arr[child] > arr[pos]){//交换两个数的位置sweap(&arr[pos], &arr[child]);//继续向下调整AdjustDown(arr, size, child);}}
}//堆排序——升序
void HeapSort(int* arr, int size)
{//从后往前依次调整建堆//先让节点的左右子树为堆,然后整体为堆int pos = (size - 1) / 2;//最后一个叶子节点父节点for (int i = pos; i >= 0; i--){//向下调整建堆AdjustDown(arr, size, i);}//堆排序//排升序要建大堆//排降序要建小堆for (int i = 0; i < size; i++){//堆顶与最后一个有效元素交换位置sweap(&arr[0], &arr[size - 1 - i]);//向下调整,保持堆的结构AdjustDown(arr, size - i - 1, 0);}
}int main()
{//给定一个乱序数组int arr[] = { 8,3,2,6,7,1,4,9,5 };//计算数组元素个数int size = sizeof(arr) / sizeof(arr[0]);//堆排序HeapSort(arr, size);//打印排序后的数据for (int i = 0; i < size; i++){printf("%d ", arr[i]);}return 0;
} 
相关文章:

八大排序算法——堆排序
目录 前言 一、向上调整算法建堆 二、向下调整算法建堆 三、堆排序 前言 堆排序是基于堆结构的一种排序思想,因此要为一个乱序的数组进行排序的前提是数组必须要是一个堆,所以要先对数组进行建堆操作 一、向上调整算法建堆 时间复杂度:O…...
U盘文件不翼而飞?这些数据恢复工具帮你找回!
U盘因其便携性是我们日常工作和生活中不可或缺的工具。不过有时候它也会出点小状况。如果你U盘里的数据突然不见了,不要着急,可以先试试这几款数据恢复工具! 福昕数据恢复 直达链接:www.pdf365.cn/foxit-restore/ 操作教程&…...

在Java中 try catch 会影响性能吗?
1、在Java中,异常处理确实会对性能产生影响,但在正常执行的代码路径中,即没有发生异常的情况下,try-catch块的性能影响是微不足道的 2、但是,如果出现异常被抛出时,Java虚拟机需要执行一些额外的操作来处理…...

吞吐量最高飙升20倍!破解强化学习训练部署难题
**强化学习(RL)对大模型复杂推理能力提升有关键作用,然而,RL 复杂的计算流程以及现有系统局限性,也给训练和部署带来了挑战。近日,字节跳动豆包大模型团队与香港大学联合提出 HybridFlow(开源项…...

redis的数据过期策略
Redis对数据设置了数据的有效时间,数据过期之后,就需要将数据从内存中删除掉.可以按照不同的规则进行删除,这种删除规则就被称之为数据的删除策略(数据过期策略),而这种策略有两种:惰性删除和定期删除 惰性删除:设置key过期时间后,我们不去管它,当需要该key时,我们在检查其是否…...

三周精通FastAPI:27 使用使用SQLModel操作SQL (关系型) 数据库
官网文档:https://fastapi.tiangolo.com/zh/tutorial/sql-databases/ SQL (关系型) 数据库 FastAPI不需要你使用SQL(关系型)数据库。 但是您可以使用任何您想要的关系型数据库。 这里我们将看到一个使用SQLModel的示例。 SQLModel是在SQLAlchemy和Pydantic的基础…...
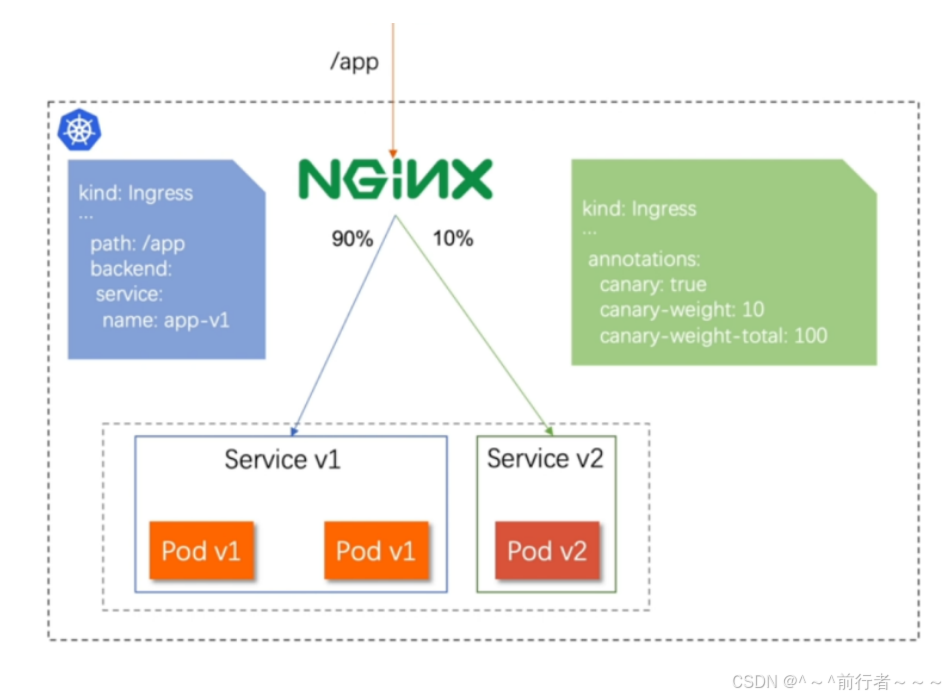
Kubernetes金丝雀发布
华子目录 Canary金丝雀发布什么是金丝雀发布Canary发布方式基于header(http包头)灰度发布基于权重的金丝雀发布 Canary金丝雀发布 什么是金丝雀发布 金丝雀发布也称为灰度发布,是一种软件发布策略主要目的是在将新版本的软件全面推广到生产环…...

树形DP讲解
文章目录 树形DP讲解一、引言二、树形DP基础1、树的定义2、树形DP的基本思想3、代码示例:子树大小 三、经典例题解析1、树的平衡点1.1、代码示例 2、没有上司的舞会(树的最大独立集)2.1、代码示例 四、总结 树形DP讲解 一、引言 树形动态规…...

容器:如何调试容器
调试容器,主要是指的调试Dockerfile,调试Dockerfile中的各个命令的执行,大小等 1、docker history查看构建过程和所有的中间层 2、docker run rm -it -u root XXX sh,通过临时容器的方式启动,可以调试中间层文件 3、do…...

用图说明 CPU、MCU、MPU、SoC 的区别
CPU CPU 负责执行构成计算机程序的指令,执行这些指令所指定的算术、逻辑、控制和输入/输出(I/O)操作。 MCU (microcontroller unit) 不同的 MCU 架构如下,注意这里的 MPU 表示 memory protection unit MPU (microprocessor un…...

牛客周赛 Round 65
文章目录 超市思路:Solved: 雨幕思路:Solved: 闺蜜思路:Solved: 医生思路:Solved: 降温(easy)思路:Solved: F-降温(hard&a…...

超级经典的79个软件测试面试题(内含答案)
1、软件的生命周期(prdctrm) 计划阶段(planning)-〉需求分析(requirement)-〉设计阶段(design)-〉编码(coding)->测试(testing)->运行与维护(running maintrnacne) 测试用例 用例编号 测试项目 测试标题 重要级别 预置条件 输入数据 执行步骤 预期结果 2、问…...

【Mac】安装 F5-TTS
1、下载项目 项目地址:【GitHub】 SWivid F5-TTS 2、创建并激活 Python 虚拟环境 # 创建 Python 虚拟环境 userMac F5-TTS-main % python3 -m venv f5-tts# 激活进入 Python 虚拟环境 userMac F5-TTS-main % source f5-tts/bin/activate (f5-tts) userrMac F5-TT…...

Leaflet查询矢量瓦片偏移的问题
1、问题现象 使用Leaflet绘制工具查询出来的结果有偏移 2、问题排查 1)Leaflet中latLngToContainerPoint和latLngToLayerPoint的区别 2)使用Leaflet查询需要使用像素坐标 3)经排查发现,container获取的坐标是地图容器坐标&…...

存储引擎技术进化
B-tree 目前支撑着数据库产业的半壁江山。 50 年来不变而且人们还没有改变它的意向 鉴定一个算法的优劣,有一个学派叫 IO复杂度分析 ,简单推演真假便知。 下面就用此法分析下 B-tree(traditional b-tree) 的 IO 复杂度,对读、写 IO 一目了…...

CentOS 9 Stream 上安装 Maven
CentOS 9 Stream 上安装 Maven 在 CentOS 9 Stream 上安装 Maven,可以按照以下步骤进行: 更新系统软件包: sudo dnf update安装 Maven: CentOS 9 Stream 默认的包管理器中已经包含 Maven,你可以直接安装: s…...

强势改进!TCN-Transformer时间序列预测
强势改进!TCN-Transformer时间序列预测 目录 强势改进!TCN-Transformer时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现TCN-Transformer时间序列预测; 2.运行环境为Matlab2023b; 3.单个变量时间序…...

MyBatis的不同参数传递封装
MyBatis参数传递 传参方式 1. 使用 #{} 占位符 这是 MyBatis 中最常用的参数传递方式。它将参数直接替换到 SQL 语句中的占位符位置。 单个参数: <select id"selectUserById" resultType"User">SELECT * FROM users WHERE id #{id}…...

kotlin 协程方法总结
Kotlin 协程是一套强大的异步编程工具,以下是对 Kotlin 协程常用方法的总结: 1. 协程构建器 launch: 启动一个新的协程,不阻塞当前线程,返回一个 Job 对象。 GlobalScope.launch {// 协程体}async: 启动一个新的协程并返回一个…...

脉冲当量计算方法
脉冲的概念: 脉冲当量是指控制器输出一个定位控制脉冲时,所产生的定位控制移动的位移。在直线运动中,它表示移动的距离;在圆周运动中,它表示转动的角度。简而言之,脉冲当量就是电机接收一个脉冲信号后能够移…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
