ubuntu-开机黑屏问题快速解决方法
-
开机黑屏一般是由于显卡驱动出现问题导致。

-
快速解决方法:
- 通过ubuntu高级选项->recovery模式->resume->按esc即可进入recovery模式,进去后重装显卡驱动,重启即可解决。
- 附加问题:
- ubuntu的默认显示管理器是gdm3,如果重装显卡驱动无法解决,还可以尝试卸载gdm3,安装lightdm。
sudo apt install lightdm #安装好备用的显示管理器
sudo service gdm3 stop #强制停止当前的gdm3进程
sudo dpkg-reconfigure lightdm #将默认的显示管理器设置成lightdm
sudo service lightdm start #立马启用新的显示管理器
sudo reboot #重启
相关文章:

ubuntu-开机黑屏问题快速解决方法
开机黑屏一般是由于显卡驱动出现问题导致。 快速解决方法: 通过ubuntu高级选项->recovery模式->resume->按esc即可进入recovery模式,进去后重装显卡驱动,重启即可解决。附加问题:ubuntu的默认显示管理器是gdm3,如果重…...

DNS服务器
正反解析 [rootlocalhost ~]# systemctl stop firewalld #关防火墙 [rootlocalhost ~]# setenforce 0 #关闭selinux [rootlocalhost ~]# mount /dev/sr0 /mnt #挂载 mount: /mnt: WARNING: source write-protected, mounted read-only. [rootlocalhost ~]# yum …...

【C++笔记】string类使用详解
前言 各位读者朋友们大家好!上期我们讲完了C的模板初阶,这一期我们开启STL的学习。STL是C的数据结构和算法库,是我们学习C的很重要的一部分内容,在以后的工作中也很重要。现在我们开始讲解。 目录 前言一. 为什么学习string类1.…...

数字隔离器与光隔离器有何不同?---腾恩科技
在电子隔离中,两种常用的解决方案是数字隔离器和光学隔离器。两者都旨在电气隔离电路的各个部分,以保护敏感元件免受高压干扰,但它们通过不同的技术实现这一目标。本文探讨了这些隔离器之间的差异,重点介绍了它们的工作原理、优势…...

方差与协方差
方差是一种特殊的协方差。...

【含文档】基于Springboot+Vue的工商局商家管理系统 (含源码数据库+LW)
1.开发环境 开发系统:Windows10/11 架构模式:MVC/前后端分离 JDK版本: Java JDK1.8 开发工具:IDEA 数据库版本: mysql5.7或8.0 数据库可视化工具: navicat 服务器: SpringBoot自带 apache tomcat 主要技术: Java,Springboot,mybatis,mysql,vue 2.视频演示地址 3.功能 系统定…...

【股票市场情绪量化模型】
股票市场情绪量化模型:理论与实践 目录 什么是股票市场情绪情绪量化模型的基本概念情绪数据的来源与获取情绪量化模型的构建 4.1 情绪指标的选择4.2 模型设计与算法 情绪与市场表现的关系情绪量化模型的应用案例模型的局限性与挑战总结 1. 什么是股票市场情绪 股…...

Oracle视频基础1.3.8与1.4.1练习
1.3.8与1.4.1 -看数据文件的目录, dump 的目录,oracle的软件目录 -(secureCRT,telnet连接linux。)看当前用户,当前所属组,通过操作系统认证以sysdba登陆,启动数据库然后关闭 -看口令文件 看数据文件的目录,…...

基于前馈神经网络模型和卷积神经网络的MINIST数据集训练
目录 前馈神经网络FNN模型 卷积神经网络CNN模型 前馈神经网络FNN模型 author: lxy function: model--mnist date : 2024/10/25 email : 13102790991163.com # 导入必要的库 import torch import torch.nn as nn import torchvision.datasets as dsets import torchvision.t…...

Vue3中Element Plus==el-eialog弹框中的input无法获取表单焦点
有弹框情况下 <template> <input ref"input" /> </template> <script setup> import { ref, onMounted } from vue // 声明一个 ref 来存放该元素的引用 // 必须和模板里的 ref 同名 const input ref(null) onMounted(() > { ne…...

16.网工入门篇--------介绍下网络服务及应用
一、网络服务的概念 网络服务是指通过网络提供的软件功能或设施,它允许不同的设备和用户在网络环境中进行信息交换、资源共享和协作。这些服务基于各种网络协议,以实现高效、可靠的通信。 二、常见网络服务类型 (一)文件传输服务 …...

区分 electron 全屏和最大化
一. 全屏 在 Electron 中,当窗口处于全屏状态时,通常不能直接使用 JavaScript 来改变窗口大小。这是出于安全和用户体验的考虑,以防止意外的窗口大小变化影响全屏体验。 1. 退出全屏后再调整大小 检测全屏状态,退出全屏并调整大…...
)
封装一个请求的hook(react函数组件)
对于后台系统,上面筛选,下面表格分页的页面,这个hook非常实用 omitBy方法:过滤不为undefined的对象属性 export const omitBy <T extends IObject, K extends keyof T>(object:T, predicate:(value:T[K]) > boolean):I…...
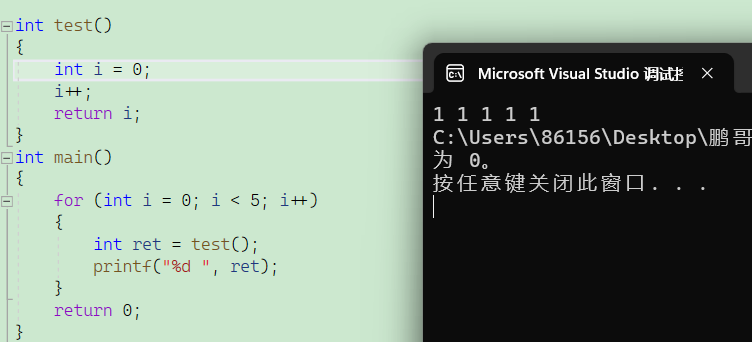
c语言内存块讲解
文章目录 前言一、栈区1、栈区的特点:1.1 自动管理1.2 后进先出1.3 有限大小1.4 高速访问1.5 栈区存储方向 2、栈区使用注意事项 二、堆区1、堆区的定义2、堆区的特点3、堆区的内存分配与释放4、注意事项: 三、全局/静态存储区1、全局存储区1.1 全局变量…...

2024年10月23日Github流行趋势
项目名称:hiteshchoudhary / apihub 项目维护者:wajeshubham, atulbhatt-system32, jwala-anirudh, arnb-smnta, shrey-dadhaniya 项目介绍:您自己的API Hub,用于学习和掌握API交互。非常适合前端、移动开发人员和后端开发人员。 …...

YOLOv6-4.0部分代码阅读笔记-dbb_transforms.py
dbb_transforms.py yolov6\layers\dbb_transforms.py 目录 dbb_transforms.py 1.所需的库和模块 2.def transI_fusebn(kernel, bn): 3.def transII_addbranch(kernels, biases): 4.def transIII_1x1_kxk(k1, b1, k2, b2, groups): 5.def transIV_depthconcat(kernel…...
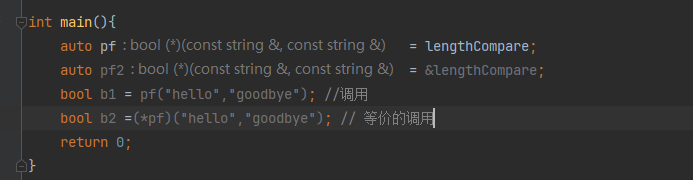
C++ 基础语法 一
C 基础语法 一 文章目录 C 基础语法 一const 限定符常量指针类型别名autodecltypeQStringvector迭代器指针和数组显示转换static_castconst_cast 函数尽量使用常量引用数组形参不要返回局部对象的引用和指针返回数组指针 C四种转换内联函数constexpr函数函数指针 const 限定符 …...

B2020 分糖果
题目描述 某个幼儿园里,有 55 位小朋友编号依次为 1,2,3,4,51,2,3,4,5 他们按照自己的编号顺序围坐在一张圆桌旁。他们身上有若干糖果,现在他们玩一个分糖果游戏。从 11 号小朋友开始,将自己的糖果均分成 33 份(如果有多余的糖果…...
VBA字典与数组第二十讲:如何在代码运行时创建数组
《VBA数组与字典方案》教程(10144533)是我推出的第三套教程,目前已经是第二版修订了。这套教程定位于中级,字典是VBA的精华,我要求学员必学。7.1.3.9教程和手册掌握后,可以解决大多数工作中遇到的实际问题。…...

字符串统计(Python)
接收键盘任意录入,分别统计大小写字母、数字及其它字符数量,打印输出。 (笔记模板由python脚本于2024年11月02日 08:23:31创建,本篇笔记适合熟悉python字符串并懂得基本编程技法的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...

可下载旧版app屏蔽更新的app市场
软件介绍 手机用久了,app越来越臃肿,老手机卡顿成常态。这里给大家推荐个改善老手机使用体验的方法,还能帮我们卸载不需要的app。 手机现状 如今的app不断更新,看似在优化,实则内存占用越来越大,对手机性…...
