二叉苹果树

AcWing 1074. 二叉苹果树【有依赖背包DP】 - AcWing
问题描述
在一棵有权无向树中,从某个节点(这里假设为节点 1)出发,遍历树的子节点,每经过一条边会获得对应的权重值。在访问节点数的限制下(即体积限制),我们希望获得最大的路径权重和。
代码解析
1. 全局变量和常量
const int N = 110, M = N << 1;
int n, m; // n 表示节点数, m 表示最大访问节点数(体积限制)
int h[N], e[M], w[M], ne[M], idx; // 邻接表
int f[N][N]; // 动态规划数组 f[u][j] 表示以 u 为根的子树中,最多选择 j 条边能得到的最大权重和
N是节点数上限,M是边数的上限。h[N]:邻接表的头节点数组,h[u]表示从u出发的第一条边在e中的索引。e[M]:邻接表存储的边的目标节点数组。w[M]:边的权重数组,表示e[i]对应边的权重。ne[M]:存储下一条边的索引。idx:记录当前插入边的位置。f[u][j]:动态规划数组,表示以u为根的子树中,选择至多j条边所能获得的最大权重和。
2. 添加边函数 add
void add(int a, int b, int c) {e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
- 该函数通过邻接表方式添加边。
a到b的边权重为c,同时更新h[a]和ne数组。
3. 深度优先搜索 dfs
void dfs(int u, int father) {for (int i = h[u]; ~i; i = ne[i]) {int ver = e[i];if (ver == father) continue;dfs(ver, u);for (int j = m; j >= 0; j--)for (int k = 0; k <= j - 1; k++)f[u][j] = max(f[u][j], f[u][j - k - 1] + f[ver][k] + w[i]);}
}
dfs是核心的递归函数。以节点u为根节点,递归处理子树中的路径选择问题。- 遍历从
u出发的每一条边,跳过回到父节点的边father。 - 调用
dfs(ver, u)递归处理子节点ver的子树,计算在ver处的最优路径权重。 - 动态规划转移:
- 外层循环
j:表示从u出发选择至多j条边。 - 内层循环
k:枚举当前子节点选择的边数。 - 转移方程
f[u][j] = max(f[u][j], f[u][j - k - 1] + f[ver][k] + w[i]);:f[u][j]:更新u节点的最优解。f[u][j - k - 1]:u剩余的边数(预留一个选择的子节点跟父节点交互时的链接)。f[ver][k]:子节点ver的最优解。w[i]:u到ver的边权。
- 外层循环
4. 主函数 main
int main() {memset(h, -1, sizeof h);scanf("%d%d", &n, &m);for (int i = 1; i < n; i++) {int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c), add(b, a, c);}dfs(1, -1);printf("%d\n", f[1][m]);return 0;
}
- 初始化邻接表头数组
h,设为-1表示空。 - 输入节点数
n和最大体积m。 - 读取并建立双向边,
add(a, b, c)和add(b, a, c)将每条边双向存储。 - 从节点
1开始进行 DFS,设-1为父节点标记,避免重复访问。 - 输出
f[1][m],即以1为根、最多选m条边所能获得的最大权重和。
相关文章:

二叉苹果树
AcWing 1074. 二叉苹果树【有依赖背包DP】 - AcWing 问题描述 在一棵有权无向树中,从某个节点(这里假设为节点 1)出发,遍历树的子节点,每经过一条边会获得对应的权重值。在访问节点数的限制下(即体积限制…...

【大数据学习 | kafka】producer的参数与结构
1. producer的结构 producer:生产者 它由三个部分组成 interceptor:拦截器,能拦截到数据,处理完毕以后发送给下游,它和过滤器不同并不是丢弃数据,而是将数据处理完毕再次发送出去,这个默认是不…...
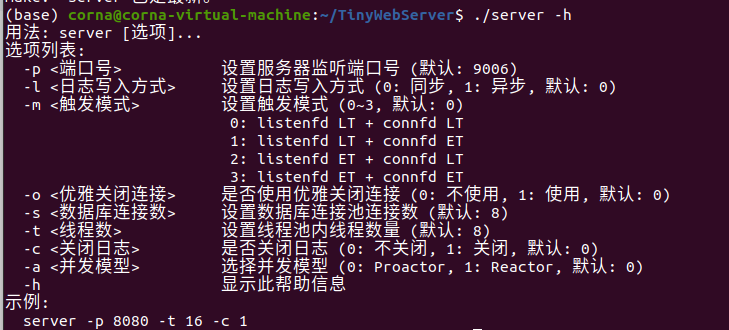
2. 从服务器的主接口入手
Webserver 的主函数 main.cpp,完成了哪些功能? #include "config.h"int main(int argc, char *argv[]) {string user "";string passwd "";string databasename "";Config config;config.parse_arg(argc, a…...

nginx上传文件超过限制大小、响应超时、反向代理请求超时等问题解决
1、文件大小超过限制 相关配置: client_max_body_size: Syntax:client_max_body_size size;Default:client_max_body_size 1m;Context:http, server, location 2、连接超时: proxy_read_timeout: Syntax:proxy_read_timeout time;Default…...

第16课 核心函数(方法)
掌握常用的内置函数及其用法。 数学类函数:abs、divmod、max、min、pow、round、sum。 类型转换函数:bool、int、float、str、ord、chr、bin、hex、tuple、list、dict、set、enumerate、range、object。 序列操作函数:all、any、filter、m…...

【工具变量】中国制造2025试点城市数据集(2000-2023年)
数据简介:《中国制造2025》是中国ZF于2015年5月8日印发的一项战略规划,旨在加快制造业的转型升级,提升制造业的质量和效益,实现从制造大国向制造强国的转变。该规划是中国实施制造强国战略的第一个十年行动纲领,明确提…...
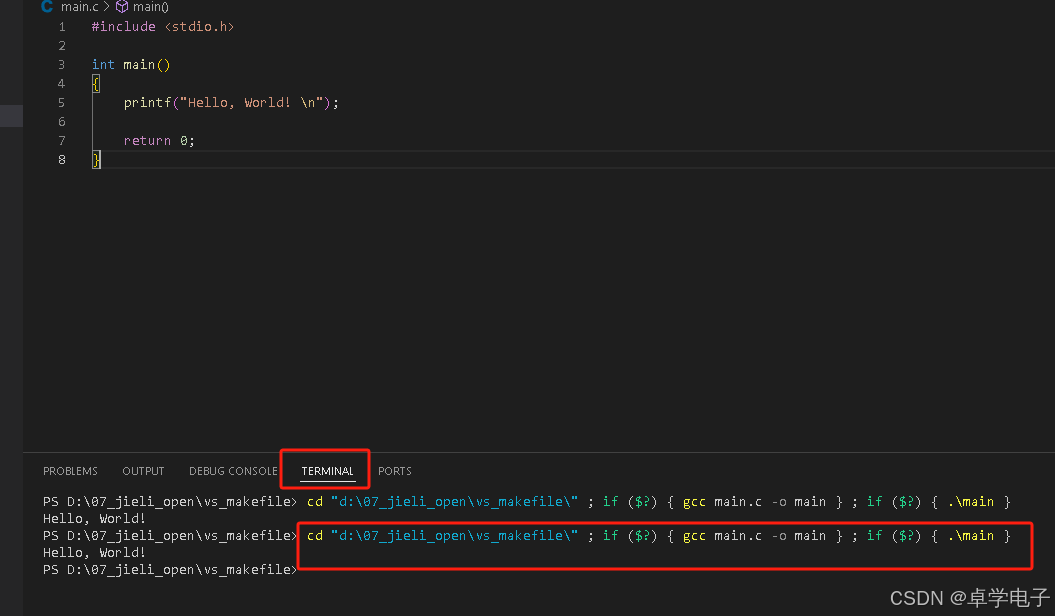
vscode makfile编译
MinGW-w64下载安装 为了在 Windows 上安装 GCC,您需要安装 MinGW-w64。 MinGW-w64 是一个开源项目,它为 Windows 系统提供了一个完整的 GCC 工具链,支持编译生成 32 位和 64 位的 Windows 应用程序。 访问 MinGW-w64 的主页 mingw-w64.org…...
PostgreSQL数据库操作示例)
(四)PostgreSQL数据库操作示例
删除有外键约束的表 最近做数据库练习遇到一个问题,数据库里面有一个表,存在外键约束,我想要删除,所以必须先删除这些外键约束。 查询外键约束 查找外键约束:当你需要知道某个表的外键约束及其引用关系时࿰…...

Docker-微服务项目部署
环境准备 1.微服务项目 参考:通过网盘分享的文件:wolf2w_cloud.zip 链接: https://pan.baidu.com/s/1Lr4k6LPIJ59gVNA_DgKM_Q?pwdkjxt 提取码: kjxt 前端项目:trip-mgrsite-ui,trip-website-ui,trip-wenda-ui 服务项…...

测试Bug提交报告模板
撰写测试Bug提交说明时,清晰、详细和准确是至关重要的。这有助于开发团队快速理解问题、重现Bug并修复它。以下是一个测试Bug提交说明的模板,可以根据实际情况进行调整: 测试Bug提交说明 1. Bug基本信息 Bug编号:[系统自动生成…...

MybatisPlus - 核心功能
文章目录 1.MybatisPlus实现基本的CRUD快速开始常见注解常见配置 2.使用条件构建造器构建查询和更新语句条件构造器自定义SQLService接口 官网 MybatisPlus无侵入和方便快捷. MybatisPlus不仅仅可以简化单表操作,而且还对Mybatis的功能有很多的增强。可以让我们的开…...
小柴冲刺软考中级嵌入式系统设计师系列二、嵌入式系统硬件基础知识(6)嵌入式系统总线及通信接口
目录 越努力,越幸运! flechazo 小柴冲刺软考中级嵌入式系统设计师系列总目录 一、PCI、PCI-E 等接口基本原理与结构 1、PCI (1)高速性。 (2)即插即用性。 (3)可靠性。 (4)复杂性。 (5)自动配置。 (6)共享中断。 (7)扩展性好。 (8)多路复用。…...

利用字典对归一化后的数据0误差还原
假设我对精度要求很高,高到无法容忍有任何误差,那么我先将x按照大小排序,然后归一化,用字典将归一化前后的x存储下来,在深度学习时使用归一化后的x进行处理,但是最后画图等处理时,我用字典取出归…...

HarmonyOS:UIAbility组件概述
一、概述 UIAbility组件是一种包含UI的应用组件,主要用于和用户交互。 UIAbility的设计理念: 原生支持应用组件级的跨端迁移和多端协同。支持多设备和多窗口形态。 UIAbility划分原则与建议: UIAbility组件是系统调度的基本单元,…...

12寸半导体厂说的华夫区是什么意思
1\什么是华夫板 在半导体行业中,“华夫区”通常指的是“华夫板”(Waffle Slab),这是一种特殊设计的楼板,其表面具有许多均匀分布的孔洞,这些孔洞形成了回风通道,用于电子芯片厂房等对空气洁净度有极高要求的环境。华夫板的设计和施工对于保证洁净室的功能发挥至关重要。…...

数据结构之链式结构二叉树的实现(进阶版)
本篇文章主要讲解链式二叉树的层序遍历以及判断是否为一棵完全二叉树 二者将会用到之前学过的队列知识,是将队列和二叉树的整合 一、如何将之前已经写好的文件加入当前的编译界面 如图所示,打开我们需要加入文件所在的文件夹,找到我们要加…...
【高等数学】3-2多元函数积分学
1. 二重积分 可以想象你有一块不规则的平面薄板,它在一个平面区域上。二重积分就是用来求这个薄板的质量(假设薄板的面密度函数是)。 把区域划分成许多非常小的小方块(类似于把一块地划分成很多小格子),在每个小方块上,密度近似看成是一个常数,然后把每个小方块的质量加…...

【传知代码】智慧医疗:纹理特征VS卷积特征
🍑个人主页:Jupiter. 🚀 所属专栏:传知代码 欢迎大家点赞收藏评论😊 目录 论文概述纹理特征和深度卷积特征算法流程数据预处理方法纹理特征提取深度卷积特征提取分类网络搭建代码复现BLS_Model.py文件——分类器搭建py…...

Python-创建并调用自定义文件中的模块/函数
背景:在Python编程中,我们常常需要创建自己的专属文件,以便帮助我们更高效,快捷地完成任务。那么在Python中我们怎么创建并调用自己文件中的模块/函数呢? 在Python中调用自定义文件,通常是指调用自己编写的Python模块…...
Kali Linux
起源与背景 Kali Linux是一个基于Debian的开源Linux发行版,专门为信息安全工作者和渗透测试员设计。它是由Offensive Security Ltd.开发和维护的,作为BackTrack的继承者而诞生。BackTrack是一个流行的安全测试发行版,但为了提供更好的支持和…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
