LeetCode 104.二叉树的最大深度
题目描述
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:3示例 2:
输入:root = [1,null,2]
输出:2提示:
- 树中节点的数量在
[0, 10^4]区间内。 -100 <= Node.val <= 100
思路
首先需要搞清楚二叉树的深度和高度是什么?
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数或者节点数(取决于高度从0开始还是从1开始)
因此,根节点的高度就是二叉树的最大深度(正因此,本题使用后序遍历来求高度)。本题笔者使用递归法来解决。
递归三部曲:
- 确定递归函数的参数和返回值。参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
- 确定终止条件。如果为空节点的话,就返回0,表示高度为0。
- 确定单层递归的逻辑。本题可以分解为先求左子树和右子树的最大高度,再加上1便是父节点的最大高度的子问题,且子问题与本问题的求解思路相同,只是规模不同,也存在终止条件,这就是本题能够使用递归法解决的关键。
代码
C++版:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:// 递归法,后序遍历求高度int getHeight(TreeNode* node){if(node==NULL) return 0;int leftHeight=getHeight(node->left); // 左int rightHeight=getHeight(node->right); // 右int height=1+max(leftHeight,rightHeight)// 中return height;}int maxDepth(TreeNode* root) {return getdepth(root);}
};Python版:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:# 递归法,后序遍历求高度def getHeight(self, node: Optional[TreeNode]) -> int:if not node:return 0leftheight = self.getHeight(node.left) # 左rightheight = self.getHeight(node.right) # 右height = 1 + max(leftheight, rightheight) # 中return heightdef maxDepth(self, root: Optional[TreeNode]) -> int:return self.getHeight(root)需要注意的地方
1.二叉树求高度需要使用后序遍历(左右中,从下往上计数+1),求深度需要使用前序遍历(中左右,从上往下计数+1)。
2.本题使用递归法解决的话也可以使用前序遍历,使用迭代法解决的话则使用层序遍历是最为合适的。
相关文章:

LeetCode 104.二叉树的最大深度
题目描述 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3 示例 2: 输入:root [1…...

Android启动流程_Init阶段
前言 本文将会介绍 Android 启动流程,将基于 Android 10 代码逻辑介绍原生启动过程。 bootloader 上电 -> 加载 recovery 镜像或者 boot 镜像 -> linux kernel 启动 -> 加载 init 进程 -> 加载 zygote 进程 -> systemserver 进程 -> 系统启动 …...

萤火虫算法优化BILSTM神经网络多输入回归分析
目录 LSTM的基本定义 LSTM实现的步骤 BILSTM神经网络 代码 结果分析 展望 完整代码下载:的MATALB代码(代码完整,数据齐全)资源-CSDN文库 https://download.csdn.net/download/abc991835105/88755564 背影 bp神经网络是一种成熟的神经网络,应用非常广,本文用萤火虫算法…...

在线QP(QuotedPrintable)编码解码工具
具体前往:Quoted-printable在线编码解码工具-将给定文本编码为:可打印字符引用编码(简称:QP编码),也支持在线解码...

【已解决】cra 配置路径别名 @ 后,出现 ts 报错:找不到模块“@/App”或其相应的类型声明。ts(2307)
cra 配置路径别名 后,出现 ts 报错:找不到模块“/App”或其相应的类型声明。ts(2307) 然后可以在 tsconfig.json 中配置 baseUrl 和 paths : {"compilerOptions": {"target": "es5","lib": [&quo…...

leetcode-643. 子数组最大平均数 I
文章目录 二 解法2.1 每次都重新计算2.2 使用窗口 给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。请你找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数。任何误差小于 10-5 的答案都将被视为正确答案。二 解法 2.1 每次都重新计算 超时 pu…...

论分布式架构设计及其实现
一、引言 随着互联网用户规模的扩大和需求的多样化,传统的集中式架构已经难以支撑高并发、高可用的系统要求。分布式架构的出现,提供了将计算和存储分布到不同服务器上的解决方案,有效提高了系统的可扩展性和容灾能力。分布式架构目前已广泛…...

基于BP神经网络的手写体数字图像识别
基于BP神经网络的手写体数字图像识别 摘要 在信息化飞速发展的时代,光学字符识别是一个重要的信息录入与信息转化的手段,其中手写体数字的识别有着广泛地应用,如:邮政编码、统计报表、银行票据等等,因其广泛地应用范围…...

QT——串口调试助手
目录 1.QSerialPort类包含了很多有关串口的API 2.实现串口的打开 2.1 方法一:通过函数实现 2.2 方法二:在ui界面右下角实现 3. 实现定时发送 3.1类的私有成员中添加定时器QTimer timer并去构造函数中初始化它 3.2帮助文档中有QTimer类相关的说明 …...
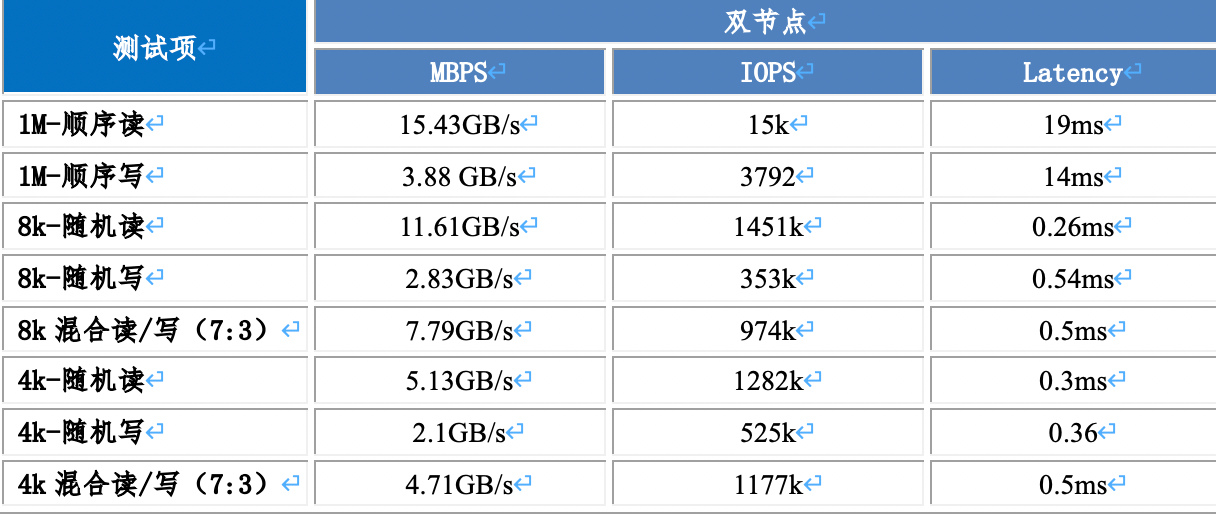
国产操作系统卖疯了!最营收7.84亿,最低1.5亿
最近看各种报道,似乎国产化有提速的绩效,那么既然如此,各个国产操作系统厂商是不是都起飞了呢? 周末闲暇之余,我们来看看各家的营收表现。 银河麒麟2024年1-9月一共卖了多少钱? 前几天中国软件发布了202…...
)
2024年华为OD机试真题-最小的调整次数-Python-OD统一考试(E卷)
最新华为OD机试考点合集:华为OD机试2024年真题题库(E卷+D卷+C卷)_华为od机试题库-CSDN博客 每一题都含有详细的解题思路和代码注释,精编c++、JAVA、Python三种语言解法。帮助每一位考生轻松、高效刷题。订阅后永久可看,发现新题及时跟新。 题目描述: 有一个特异性的…...

React.js教程:从JSX到Redux的全面解析
文章目录 介绍react脚手架jsx语法和react组件jsx的基本语法jsx的行内样式jsx的类名classNameif条件渲染map循环渲染创建组件方法 可视区渲染 (React- virtualized)React-redux 介绍 javascript库,起源于Facebook的内部项目,类似于vue特点 声明式组件化 …...

二叉苹果树
AcWing 1074. 二叉苹果树【有依赖背包DP】 - AcWing 问题描述 在一棵有权无向树中,从某个节点(这里假设为节点 1)出发,遍历树的子节点,每经过一条边会获得对应的权重值。在访问节点数的限制下(即体积限制…...

【大数据学习 | kafka】producer的参数与结构
1. producer的结构 producer:生产者 它由三个部分组成 interceptor:拦截器,能拦截到数据,处理完毕以后发送给下游,它和过滤器不同并不是丢弃数据,而是将数据处理完毕再次发送出去,这个默认是不…...
2. 从服务器的主接口入手
Webserver 的主函数 main.cpp,完成了哪些功能? #include "config.h"int main(int argc, char *argv[]) {string user "";string passwd "";string databasename "";Config config;config.parse_arg(argc, a…...

nginx上传文件超过限制大小、响应超时、反向代理请求超时等问题解决
1、文件大小超过限制 相关配置: client_max_body_size: Syntax:client_max_body_size size;Default:client_max_body_size 1m;Context:http, server, location 2、连接超时: proxy_read_timeout: Syntax:proxy_read_timeout time;Default…...

第16课 核心函数(方法)
掌握常用的内置函数及其用法。 数学类函数:abs、divmod、max、min、pow、round、sum。 类型转换函数:bool、int、float、str、ord、chr、bin、hex、tuple、list、dict、set、enumerate、range、object。 序列操作函数:all、any、filter、m…...

【工具变量】中国制造2025试点城市数据集(2000-2023年)
数据简介:《中国制造2025》是中国ZF于2015年5月8日印发的一项战略规划,旨在加快制造业的转型升级,提升制造业的质量和效益,实现从制造大国向制造强国的转变。该规划是中国实施制造强国战略的第一个十年行动纲领,明确提…...
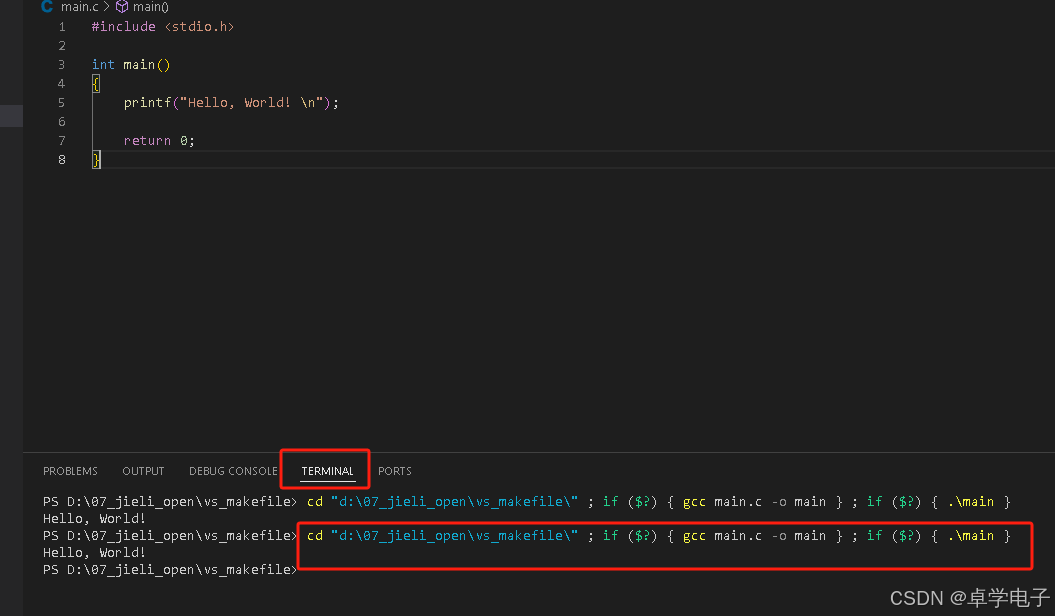
vscode makfile编译
MinGW-w64下载安装 为了在 Windows 上安装 GCC,您需要安装 MinGW-w64。 MinGW-w64 是一个开源项目,它为 Windows 系统提供了一个完整的 GCC 工具链,支持编译生成 32 位和 64 位的 Windows 应用程序。 访问 MinGW-w64 的主页 mingw-w64.org…...
PostgreSQL数据库操作示例)
(四)PostgreSQL数据库操作示例
删除有外键约束的表 最近做数据库练习遇到一个问题,数据库里面有一个表,存在外键约束,我想要删除,所以必须先删除这些外键约束。 查询外键约束 查找外键约束:当你需要知道某个表的外键约束及其引用关系时࿰…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
