LeetCode --- 421周赛
题目列表
3334. 数组的最大因子得分
3335. 字符串转换后的长度 I
3336. 最大公约数相等的子序列数量
3337. 字符串转换后的长度 II
一、数组的最大因子得分

数据范围足够小,可以用暴力枚举移除的数字,得到答案,时间复杂度为O(n^2),代码如下
class Solution {
public:long long maxScore(vector<int>& nums) {int n = nums.size();auto get = [&](int i)->long long{// gcd(0, x) = x, lcm(1, x) = xlong long x = 0; // 计算 gcdlong long y = 1; // 计算 lcmfor(int j = 0; j < n; j++){if(i == j) continue;x = gcd(x, nums[j]);y = lcm(y, nums[j]);}return x * y;};long long ans = get(-1); // 不去除任何数字for(int i = 0; i < n; i++){ans = max(ans, get(i));}return ans;}
};有没有更快的做法?我们同样枚举被移除的数字,有没有方法能更加快速的算出剩余数字的 LCM 和 GCD?有的,只要我们提前算出左右两个部分的 LCM 和 GCD,就能直接计算得出剩余部分的LCM 和 GCD,即进行前后缀分解,时间复杂度为O(n),代码如下
注意:上面的时间复杂度默认 LCM 和 GCD 是O(1),但实际上 GCD/LCM 的时间复杂度为O(logn)
class Solution {
public:long long maxScore(vector<int>& nums) {int n = nums.size();vector<long long> suf_gcd(n + 1), suf_lcm(n + 1, 1);// gcd(0, x) = x, lcm(1, x) = xfor(int i = n - 1; i >= 0; i--){suf_gcd[i] = gcd(suf_gcd[i + 1], nums[i]);suf_lcm[i] = lcm(suf_lcm[i + 1], nums[i]);}long long ans = suf_gcd[0] * suf_lcm[0]; // 不去除任何数long long pre_gcd = 0, pre_lcm = 1;for(int i = 0; i < n; i++){ // 同时计算 ans 和 前缀gcd/lcmans = max(ans, gcd(pre_gcd, suf_gcd[i + 1]) * lcm(pre_lcm, suf_lcm[i+1]));pre_gcd = gcd(pre_gcd, nums[i]);pre_lcm = lcm(pre_lcm, nums[i]);}return ans;}
};二、字符串转换后的长度 I

这题的数据范围比较小,我们可以模拟 t 次转换的过程。对于任意一个字母,它的转换规则是一样的,所以我们先统计出 26 个字母出现的次数,然后根据规则,进行转换即可,代码如下
class Solution {const int MOD = 1e9 + 7;
public:int lengthAfterTransformations(string s, int t) {vector<int> cnt(26);for(auto e : s) cnt[e - 'a']++;while(t--){vector<int>tmp(26);for(int i = 0; i < 26; i++)tmp[i] = cnt[(i-1+26)%26]; // 如'a'的出现次数变成'b'的出现次数// 'z' 不仅能变成 'a' , 还能变成 'b'tmp[1] =(tmp[1] + cnt[25]) % MOD;swap(tmp, cnt);}int ans = 0;for(int i = 0; i < 26; i++) ans = (ans + cnt[i]) % MOD;return ans;}
};但是一旦 t 的范围过大,就会超时,有没什么更快的方法?由于每个字母的转移方式是固定的,所以只要给定一个字母和操作次数就能得到一个长度,问题是如何加速这个计算过程?
假设f[i][j]表示字母 i (用0-25表示) 经过 j 次操作的长度,我们有如下方程

代码如下
class Solution {const int MOD = 1e9 + 7;// 矩阵快速幂vector<vector<int>> POW(vector<vector<int>> a, int n){int m = a.size();vector<vector<int>> res(m, vector<int>(m));for(int i = 0; i < m; i++) res[i][i] = 1;while(n){if(n & 1) res = mul(res, a);a = mul(a, a);n >>= 1;}return res;}// 矩阵相乘vector<vector<int>> mul(const vector<vector<int>>& a, const vector<vector<int>>& b){int n = a.size(), m = b[0].size();vector<vector<int>> c(n, vector<int>(m));for(int i = 0; i < n; i++){for(int k = 0; k < n; k++){if(a[i][k] == 0) continue;for(int j = 0; j < m; j++){c[i][j] = (c[i][j] + 1LL * a[i][k] * b[k][j]) % MOD;}}}return c;}
public:int lengthAfterTransformations(string s, int t) {int n = s.size();vector<vector<int>> mtx(26, vector<int>(26));for(int i = 0; i < 26; i++){mtx[i][(i+1)%26] = 1;}mtx[25][1] = 1;auto f = POW(mtx, t); // 矩阵的t次幂vector<int> cnt(26);for(auto e : s) cnt[e - 'a']++;long long ans = 0;for(int i = 0; i < 26; i++){ans += reduce(f[i].begin(), f[i].end(), 0LL) * cnt[i];}return ans % MOD;}
};三、最大公约数相等的子序列数量

对于每一个数,都有三种可能,要么在seq1,要么在seq2,要么不选,一旦我们选择完一个数,对于剩下的数,我们依旧可以用相同的方法进行处理,大问题被划分为一个个小问题,进行解决。
设dfs(i,j,k)表示当seq1的gcd=j,seq2的gcd=k时,从前 i 个数中进行选择能得到的合法方案数
对于 nums[i]
- 1、不选,方案数为 dfs(i-1,j,k)
- 2、选入seq1,方案数为 dfs(i-1,gcd(j,nums[i]),k)
- 3、选入seq2,方案数为 dfs(i-1,j,gcd(k,nums[i]))
故状态转换方程为
dfs(i,j,k) = dfs(i-1,j,k) + dfs(i-1,gcd(j,nums[i]),k) + dfs(i-1,j,gcd(k,nums[i]))
边界条件:当 i < 0 时,返回 j == k,表示将所有的数都进行分配后,如果seq1的gcd = seq2的gcd,则为一种合法方案数
代码如下
class Solution {const int MOD = 1e9 + 7;
public:int subsequencePairCount(vector<int>& nums) {int n = nums.size();int memo[n][201][201];memset(memo, -1, sizeof(memo));function<int(int,int,int)> dfs = [&](int i, int j, int k)->int{if(i < 0) return j == k;if(memo[i][j][k] != -1) return memo[i][j][k];int res = dfs(i - 1, j, k); // 不选res = (res + dfs(i - 1, gcd(j, nums[i]), k)) % MOD;res = (res + dfs(i - 1, j, gcd(k, nums[i]))) % MOD;return memo[i][j][k] = res;};// 注意我们的dfs会包含一种seq1和seq2都为空的方案,需要被减去// 由于取模操作 dfs(n - 1, 0, 0) - 1 可能为负数,所以要 + MOD) % MODreturn (dfs(n - 1, 0, 0) - 1 + MOD) % MOD;}
};四、字符串转换后的长度 II

这题的思路同第二题,只是计算的矩阵不同,具体代码如下
class Solution {const int MOD = 1e9 + 7;// 矩阵快速幂vector<vector<int>> POW(vector<vector<int>> a, int n){int m = a.size();vector<vector<int>> res(m, vector<int>(m));for(int i = 0; i < m; i++) res[i][i] = 1;while(n){if(n & 1) res = mul(res, a);a = mul(a, a);n >>= 1;}return res;}// 矩阵相乘vector<vector<int>> mul(const vector<vector<int>>& a, const vector<vector<int>>& b){int n = a.size(), m = b[0].size();vector<vector<int>> c(n, vector<int>(m));for(int i = 0; i < n; i++){for(int k = 0; k < n; k++){if(a[i][k] == 0) continue;for(int j = 0; j < m; j++){c[i][j] = (c[i][j] + 1LL * a[i][k] * b[k][j]) % MOD;}}}return c;}
public:int lengthAfterTransformations(string s, int t, vector<int>& nums) {int n = s.size();vector<vector<int>> mtx(26, vector<int>(26));for(int i = 0; i < 26; i++){for(int j = i + 1; j <= i + nums[i]; j++){mtx[i][j%26] = 1;}}auto f = POW(mtx, t);vector<int> cnt(26);for(auto e : s) cnt[e - 'a']++;long long ans = 0;for(int i = 0; i < 26; i++){ans += reduce(f[i].begin(), f[i].end(), 0LL) * cnt[i];}return ans % MOD;}
};相关文章:

LeetCode --- 421周赛
题目列表 3334. 数组的最大因子得分 3335. 字符串转换后的长度 I 3336. 最大公约数相等的子序列数量 3337. 字符串转换后的长度 II 一、数组的最大因子得分 数据范围足够小,可以用暴力枚举移除的数字,得到答案,时间复杂度为O(n^2)&#…...

简单了解前缀树/字典树(Trie树)C++代码
介绍Trie树 Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补全和拼写检查。 前缀树也有一些其它的名称:字典…...

ubuntu安装与配置Nginx(2)
1. 配置 Nginx Nginx 的配置文件通常位于 /etc/nginx/nginx.conf,而虚拟主机的配置文件通常在 /etc/nginx/sites-available/ 和 /etc/nginx/sites-enabled/ 目录中。 在/etc/nginx/conf.d目录下新建xx.conf文件,配置文件, nginx -t 检查语法…...
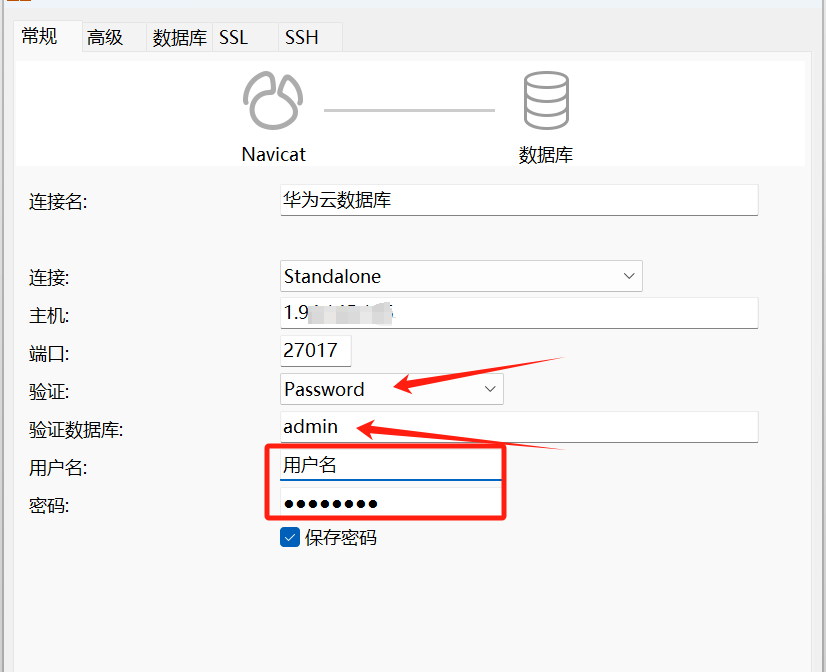
Linux环境下Mongodb部署
文章目录 一、系统环境二、MongoDb安装添加MongoDB官方库安装MongoDB配置MongoDB 三、MongoDB常见操作四、MongoDB用户管理创建用户修改密码删除用户 五、启用安全控制六、备份与还原1. 备份2. 恢复 七、外部工具连接MongoDB 一、系统环境 CentOS Stream 9 64bit 二、MongoD…...

(九)JavaWeb后端开发——Servlet
目录 1.Servlet由来 2.Servlet快速入门 3.Servlet执行原理 4.Servlet生命周期 1.Servlet由来 在JaveEE API文档中对Servlet的描述是:可以运行在服务器端的微小程序,但是实际上,Servlet就是一个接口,定义了Java类被浏览器访问…...

【零售和消费品&家居用品】家庭门窗开闭状态安全监控系统源码&数据集全套:改进yolo11-DCNV2
改进yolo11-GhostDynamicConv等200全套创新点大全:家庭门窗开闭状态安全监控系统源码&数据集全套 1.图片效果展示 项目来源 人工智能促进会 2024.11.01 注意:由于项目一直在更新迭代,上面“1.图片效果展示”和“2.视频效果展示”…...

【JavaScript】axios 二次封装拦截器(接口、实例、全局)
学习 coderwhy 老师结合 ts 二次封装 axios 目录结构 config config\index.ts // export const BASE_URL "http://codercba.com:9002"; export const TIME_OUT 10000;// 1. 根据环境变量区分接口地址 // let BASE_URL: string; // if (process.env.NODE_ENV &qu…...

Linux_02 Linux常用软件——vi、vim
vi编辑器有三种主要模式,每种模式的功能和用途不同: 一、命令模式 (Command Mode): - 启动 vi 时默认进入此模式。 - 你可以在此模式下移动光标,输入各种命令(如删除、复制、粘贴等)。 yy:…...

C++代码优化--要求或禁止在堆中产生对象
目录 1.引言 2.栈与堆区别 2.1. 栈(Stack) 2.2. 堆(Heap) 3.限制在堆上分配内存的好处 4.对象在栈上分配内存的方法 4.1. 使用RAII(资源获取即初始化) 4.2. 避免使用new和delete 4.3. 限制对象的生…...

MybatisPlus入门(六)MybatisPlus-空值处理
一、MybatisPlus-空值处理 1.1)问题引入: 在查询中遇到如下情况,有部分筛选条件没有值,如商品价格有最大值和最小值,商品价格部分时候没有值。 1.2)解决办法: 步骤一:新建查询实体…...

钉钉内集成第三方免密登录(Vue+.Net)
需要实现的效果就是在钉钉内点击应用能跳转到第三方网站并且免密登录 1.登录钉钉PC端管理后台 2.通过管理后台进去开发者后台 3.应用开发 创建H5微应用 4.应用创建成功后直接点权限管理全部授权 5.设置H5登录地址 6. 应用管理发布 至此需要配置的步骤全部已完成,…...

卷积神经网络实验三:模型优化(1)
作者有话说: 这篇文章写的还是比混乱的。因为本人也是第一次做这样的尝试,虽然接触深度学习有一年了,但是对于模型的优化仅仅是局限于理论上。通过这一次的实验,我对于模型的理解也更深了几分。我不期望这篇文章能帮你能解决多大问…...

STM32F103的CAN通讯接收测试
首先配置CUBEMX 1.打开CUBEMX 设置时钟,由于我没有外部时钟,所以我选择内部时钟,选择8倍频,1分频,APB1时钟频率为32MKHZ,也就是说每秒能够执行 3200 万个时钟周期,1M是每秒执行100万个时钟周期。 2.CAN收…...

【Rust中的智能指针】
Rust中的智能指针 什么是智能指针?什么是Rust中的智能指针?Rust中的智能指针BoxBox的使用场景 Rust中的智能指针Rc与Arcrust中的RefCellrefcell的缺点:rust中的weak先来看看C中的weak_ptr定义代码示例: Deref和Drop 总结 什么是智…...

基于深度学习的社交网络中的社区检测
在社交网络分析中,社区检测是一项核心任务,旨在将网络中的节点(用户)划分为具有高内部连接密度且相对独立的子群。基于深度学习的社区检测方法,通过捕获复杂的网络结构信息和节点特征,在传统方法基础上实现…...

【Python基础】
一、编程语言介绍 1、分类 机器语言 (直接用 0 1代码编写)汇编语言 (英文单词替代二进制指令)高级语言 2、总结 1、执行效率:机器语言>汇编语言>高级语言(编译型>解释型) 2、开发效率&…...
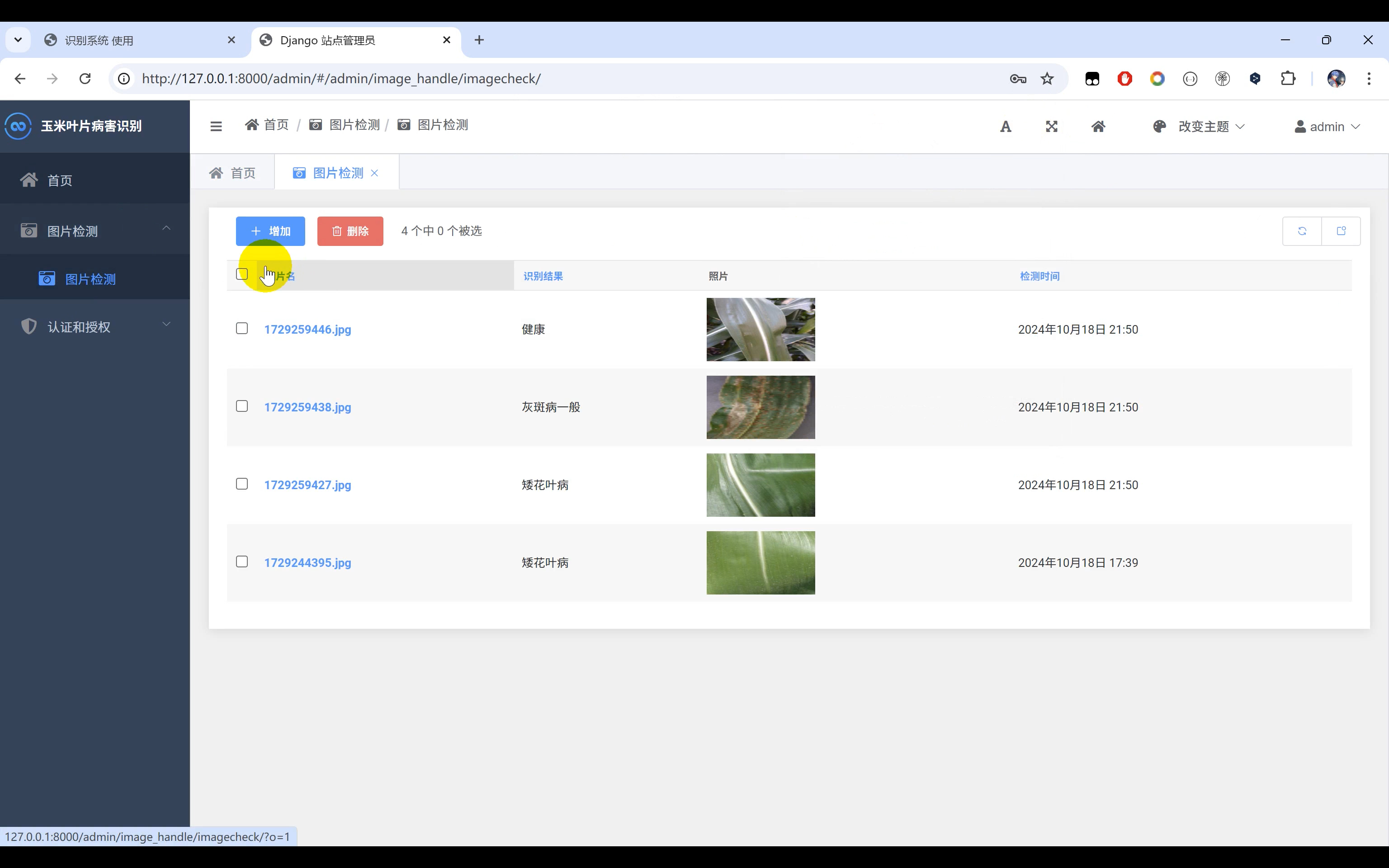
【玉米叶部病害识别】Python+深度学习+人工智能+图像识别+CNN卷积神经网络算法+TensorFlow
一、介绍 玉米病害识别系统,本系统使用Python作为主要开发语言,通过收集了8种常见的玉米叶部病害图片数据集(‘矮花叶病’, ‘健康’, ‘灰斑病一般’, ‘灰斑病严重’, ‘锈病一般’, ‘锈病严重’, ‘叶斑病一般’, ‘叶斑病严重’&#x…...

【设计模式】如何用C++实现依赖倒置
【设计模式】如何用C实现依赖倒置 一、什么是依赖倒置? 依赖倒置原则(Dependency Inversion Principle,DIP)是SOLID面向对象设计原则中的一项。它的核心思想是: 高层模块不应该依赖于低层模块,两者都应该…...

使用onnxruntime-web 运行yolov8-nano推理
ONNX(Open Neural Network Exchange)模型具有以下两个特点促成了我们可以使用onnxruntime-web 直接在web端上运行推理模型,为了让这个推理更直观,我选择了试验下yolov8 识别预览图片: 1. 跨平台兼容性 ONNX 是一种开…...
格式视频)
Gin框架html/vue前端使用hls.js播放/点播m3u8(hls)格式视频
说明 在web应用开发时遇到在线播放m3u8格式视频,由于m3u8是多分片视频,原生video标签无法直接播放,所以需要js对m3u8处理才能播放,网上有很多插件,这里我选择最近简单方法hls.js播放,引入一个js文件即可。…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
