求最大公约数,最小公倍数
输入两个正整数
m和n,求其最大公约数和最小公倍数。
求最小公倍数算法:
最小公倍数 = 两整数的乘积 ÷ 最大公约数
根据求最小公倍数的算法,可以看出如果已知最大公约数,就能很容易求出最小公倍数。而通过辗转相除法和相减法,可以求得最大公约数,下面分别进行介绍。
代码如下:
#include<stdio.h>
int main()
{int m,n;//定义两个整数scanf("%d %d",&m,&n);int max,min;int a,b;//找出较小值a,较大值ba=m<n?m:n;//若m<n成立,则输出m,若不成立,则输出nb=m>n?m:n;//若m>n成立,则输出m,若不成立,则输出nfor(int i=1;i<=a;i++)循环1到较小数范围内的数{if(a%i==0&&b%i==0)能被同时整除{max=i;最大公约数}}min=m*n/max;//最小公倍数printf("最大公约数是:%d\n最小公倍数是:%d", max, min);return 0;
}相关文章:

求最大公约数,最小公倍数
输入两个正整数 m 和 n,求其最大公约数和最小公倍数。 求最小公倍数算法: 最小公倍数 两整数的乘积 最大公约数 根据求最小公倍数的算法,可以看出如果已知最大公约数,就能很容易求出最小公倍数。而通过辗转相除法和相减法&#…...

Android——横屏竖屏
系统配置变更的处理机制 为了避免横竖屏切换时重新加载界面的情况,Android设计了一中配置变更机制,在指定的环境配置发生变更之时,无需重启活动页面,只需执行特定的变更行为。该机制的视线过程分为两步: 修改 Androi…...

scala---10.30
val、var package com_1030class Person {var name:String"rose"def sum(n1:Int,n2:Int):Int{n1n2} } object Person{def main(args: Array[String]): Unit {//创建person对象var personnew Person()println(person.sum(10,20))//30println(person.name)person.nam…...
Pinctrl子需要中client端使用pinctrl过程的驱动分析
往期内容 本专栏往期内容: Pinctrl子系统和其主要结构体引入Pinctrl子系统pinctrl_desc结构体进一步介绍Pinctrl子系统中client端设备树相关数据结构介绍和解析inctrl子系统中Pincontroller构造过程驱动分析:imx_pinctrl_soc_info结构体 input子系统专栏…...

【网络】传输层协议TCP
目录 四位首部长度 序号 捎带应答 标记位 超时重传机制 连接管理机制(RST标记位) 三次握手及四次挥手的原因 TCP的全称是传输控制协议(Transmission Control Protocol),也就是说,对于放到TCP发送缓冲…...
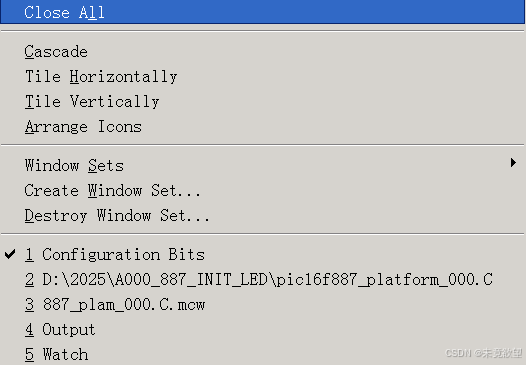
00-开发环境 MPLAB IDE 配置
MPLAB IDE V8.83 File 菜单简介 New (CtrlN): 创建一个新文件,用于编写新的代码。 Add New File to Project...: 将新文件添加到当前项目中。 Open... (CtrlO): 打开现有文件。 Close (CtrlE): 关闭当前打开的文件。 …...

<meta property=“og:type“ content=“website“>
<meta property"og:type" content"website"> 这段代码是HTML中的一部分,具体来说,它是一个用于定义Open Graph协议的meta标签。 代码分析 <meta> 标签:这是一个HTML标签,用于在HTML文档的头…...

C++ 实现俄罗斯方块游戏
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

QT打包Macosx应用发布App Store简易流程
1、QC里编译工程,生成Release版的的app文件; 2、运行macdeployqt把需要的文件打包进app文件中; % ~/Qt/5.15.0/clang_64/bin/macdeployqt {编译的app文件所在路径}/Release/xxxx.app 3、使用codesign对app进行签名,如果要发App…...

untiy mlagents 飞机大战 ai训练
前言 之前那个python源码的飞机大战bug过多,还卡顿,难以继续训练。可直接放弃的话又不甘心,所以找了个unity版本的飞机大战继续(终于不卡了),这次直接使用现成的mlagents库。 过程 前前后后花了两周时间,甚至因此拖…...

从0开始学统计-什么是中心极限定理
引言 中心极限定理(Central Limit Theorem, CLT)是统计学中的一块基石,它揭示了一个难以置信的数学现象:无论一个随机变量的原始分布如何,只要我们取足够大的样本量,这些样本的平均值(或总和&a…...

工具方法 - 个人活动的分类
人类活动的分类是一个复杂的话题,因为人类的活动范围非常广泛且相互交叉。然而,我们可以尝试将人类的活动大致分为以下几个主要类别: 工作活动 工作活动是人类生活中不可或缺的一部分,通常包括以下方面: 1. 职业工作&a…...

11.1组会汇报-基于区块链的安全多方计算研究现状与展望
基础知识 *1.背书,这个词源来自银行票据业务,是指票据转让时,原持有人在票据背面加盖自己的印鉴,证明该票据真实有效、如果有问题就可以找原持有人。 区块链中的背书就好理解了。可以简单的理解为验证交易并声明此交易合法&…...

ubuntu【桌面】 配置NAT模式固定IP
DHCP分配导致虚拟机IP老变,SSH老要重新配置,设成静态方便些 一、设NAT模式 1、设为NAT模式 2、看模式对应的虚拟网卡 - VMnet8 3、共享主机网卡网络到虚拟网卡 - VMnet8 二、为虚拟网卡设置静态IP 记住这个IP 三、设置ubuntu固定IP 1、关闭DHCP并…...

评估 机器学习 回归模型 的性能和准确度
回归 是一种常用的预测模型,用于预测一个连续因变量和一个或多个自变量之间的关系。 那么,最后评估 回归模型 的性能和准确度非常重要,可以帮助我们判断模型是否有效并进行改进。 接下来,和大家分享如何评估 回归模型 的性能和准…...

如何下载安装TestLink?
一、下载TestLink、XAMPP TestLink 下载 |SourceForge.net 备用:GitHub - TestLinkOpenSourceTRMS/testlink-code: TestLink开源测试和需求管理系统 下载XAMPP: Download XAMPP 注意:TestLink与PHP版本有关系,所以XA…...

基于SSM+微信小程序的订餐管理系统(点餐2)
👉文末查看项目功能视频演示获取源码sql脚本视频导入教程视频 1、项目介绍 基于SSM微信小程序的订餐管理系统实现了管理员和用户。管理端实现了 首页、个人中心、用户管理、菜品分类管理、菜品信息管理、订单信息管理、配送信息管理、菜品评价管理、订单投诉管理、…...

【C++排序 双指针】1996. 游戏中弱角色的数量|1996
本文涉及的基础知识点 排序 C算法:滑动窗口及双指针总结 本题其它解法 【C单调栈 排序】1996. 游戏中弱角色的数量|1996 LeetCode1996. 游戏中弱角色的数量 你正在参加一个多角色游戏,每个角色都有两个主要属性:攻击 和 防御 。给你一个…...

GESP4级考试语法知识(捕捉异常)
参考程序代码: #include <iostream> using namespace std;double divide(double a, double b) {if (b 0) {throw "Division by zero error"; // 抛出异常}return a / b; }int main() {double num1, num2;cout << "Enter two numbers:…...

HTML 基础标签——元数据标签 <meta>
文章目录 1. `<meta>` 标签概述2. 属性详解2.1 `charset` 属性2.2 `name` 属性2.3 `content` 属性2.4 `http-equiv` 属性3. 其他常见属性小结在 HTML 文档中,元数据标签 <meta> 是一种重要的标签,用于提供关于文档的信息,这些信息不直接显示在网页内容中,但对于…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
