计算机视觉实验一:图像基础处理
1. 图像的直方图均衡
1.1 实验目的与要求
(1)理解直方图均衡的原理与作用;
(2)掌握统计图像直方图的方法;
(3)掌握图像直方图均衡的方法。
1.2 实验原理及知识点
直方图均衡化是通过灰度变换将一幅图象转换为另一幅均衡直方图,即在每个灰度级上都具有相同的象素点数的过程。图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。直方图拉伸是通过对比度拉伸对直方图进行调整,从而“扩大”前景和背景灰度的差别,以达到增强对比度的目的,这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。直方图均衡的缺点是:1、变换后图像的灰度级减少,某些细节消失;2、某些图像,如直方图有高峰,经处理后对比度不自然的过分增强。
1.3 实验仪器与软件
(1) PC计算机
(2) MatLab或opencv
(3) 实验所需要的图片 (注意: 示例代码中的如 rice.png,pout.tif 等图片一般可以直接使用不需要准备,这些图片是安装matlab后就有的示例图片,如果读不了可以尝试修改一下文件名的后缀,如.png,.jpg或者.tif,也可以在本报告中另存图片在工作目录上)
1.4 实验报告要求
描述实验的基本步骤,用数据和图片给出各个步骤中取得的实验结果和源代码,并进行必要的讨论,必须包括原始图像及其计算/处理后的图像。
1.5 实验内容及步骤
(1) 直方图显示
读入图像‘rice.png’,在一个窗口中显示灰度级n=64,128和256的图像直方图。
% 读入图像
image = imread('rice.png');
% 显示灰度级为64的直方图
subplot(3,1,1);
imhist(image, 64);
title('Histogram with 64 Gray Levels');
% 显示灰度级为128的直方图
subplot(3,1,2);
imhist(image, 128);
title('Histogram with 128 Gray Levels');
% 显示灰度级为256的直方图
subplot(3,1,3);
imhist(image, 256);
title('Histogram with 256 Gray Levels');
(2)直方图灰度调节
利用函数imadjust调解图像灰度范围,观察变换后的图像及其直方图的变化。
% 读入图像
image = imread('rice.png');
% 对图像进行灰度范围调节
adjusted_image = imadjust(image);
% 显示原图像
subplot(2,2,1);
imshow(image);
title('Original Image');
% 显示原图像的直方图
subplot(2,2,2);
imhist(image);
title('Original Histogram');
% 显示调节后的图像
subplot(2,2,3);
imshow(adjusted_image);
title('Adjusted Image');
% 显示调节后的图像的直方图
subplot(2,2,4);
imhist(adjusted_image);
title('Adjusted Histogram');
(3)直方图均衡化
分别对图像‘pout.tif’和‘tire.tif’进行直方图均衡化处理,比较处理前后图像及直方图分布的变化。
% 读入图像1
image1 = imread('pout.tif');% 读入图像2
image2 = imread('tire.tif');% 对图像1进行直方图均衡化
equalized_image1 = histeq(image1);% 对图像2进行直方图均衡化
equalized_image2 = histeq(image2);% 显示处理前的图像和直方图
subplot(2,4,1);
imshow(image1);
title('Original Image 1');subplot(2,4,2);
imhist(image1);
title('Original Histogram 1');subplot(2,4,5);
imshow(image2);
title('Original Image 2');subplot(2,4,6);
imhist(image2);
title('Original Histogram 2');% 显示处理后的图像和直方图
subplot(2,4,3);
imshow(equalized_image1);
title('Equalized Image 1');subplot(2,4,4);
imhist(equalized_image1);
title('Equalized Histogram 1');subplot(2,4,7);
imshow(equalized_image2);
title('Equalized Image 2');subplot(2,4,8);
imhist(equalized_image2);
title('Equalized Histogram 2');
(4)读取一幅彩色图像(图片自己准备),对RGB图像的每个通道进行直方图均衡化,对均衡化后进行重新合并成彩色图像,展示不同阶段的图像效果。另将RGB图像转换为HSV图像(rgb2hsv函数),分别对三分量的图像行直方图均衡化,最后合并成新的彩色图像,分析不同阶段的图像效果。
% 读入彩色图像
rgb_image = imread('你的图片文件路径');% 对RGB图像的每个通道进行直方图均衡化
equalized_R = histeq(rgb_image(:,:,1));
equalized_G = histeq(rgb_image(:,:,2));
equalized_B = histeq(rgb_image(:,:,3));% 合并三个通道成彩色图像
equalized_rgb_image = cat(3, equalized_R, equalized_G, equalized_B);% 显示不同阶段的图像效果
subplot(2,3,1);
imshow(rgb_image);
title('Original RGB Image');subplot(2,3,2);
imshow(equalized_R);
title('Equalized Red Channel');subplot(2,3,3);
imshow(equalized_G);
title('Equalized Green Channel');subplot(2,3,4);
imshow(equalized_B);
title('Equalized Blue Channel');subplot(2,3,5);
imshow(equalized_rgb_image);
title('Equalized RGB Image');% 将RGB图像转换为HSV图像
hsv_image = rgb2hsv(rgb_image);% 分别对HSV图像的三分量进行直方图均衡化
equalized_h = histeq(hsv_image(:,:,1));
equalized_s = histeq(hsv_image(:,:,2));
equalized_v = histeq(hsv_image(:,:,3));% 合并三个通道成新的彩色图像
equalized_hsv_image = cat(3, equalized_h, equalized_s, equalized_v);% 转回RGB图像
equalized_rgb_from_hsv = hsv2rgb(equalized_hsv_image);% 显示不同阶段的图像效果
figure;
subplot(1,2,1);
imshow(equalized_rgb_image);
title('Equalized RGB Image');subplot(1,2,2);
imshow(equalized_rgb_from_hsv);
title('Equalized RGB Image from HSV');
(5)自行设计程序实现图像的直方图均衡(选做,即不使用matlab或其它库内的相关函数实现)。
选做就是不做
2. 图像的形态学操作
2.1 实验目的与要求
目的:学习常见的数学形态学运算基本方法,了解腐蚀、膨胀、开运算、闭运算取得的效果,培养处理实际图像的能力。
2.2 实验原理及知识点
数学形态学是一种基于形状的图像处理理论和方法,数学形态学图像处理的基本思想是选择具有一定尺寸和形状的结构元素,并提取图像中相关形状结构的图像分量,以达到对图像分析和识别的目的。
膨胀和腐蚀是数学形态学图像处理的两个基本运算,其他数学形态学运算或算法均是以这两种基本运算为基础。二值图像形态学的基本运算包括膨胀、腐蚀、开运算、闭运算和击中击不中运算。在基本运算的基础上设计了多种二值形态学的实用算法,例如,去噪、边界提取、孔洞填充、连通分量的提取、骨架、凸包、细化、粗化、剪枝。灰度形态学的基本运算包括灰度膨胀、灰度腐蚀、灰度的开运算和闭运算,在基本的运算的基础上,灰度图像形态学的主要算法有顶帽变换、底帽变换和灰度形态学重构。数学形态学算法具有利于并行实现的结构,适合于并行操作,且硬件上容易实现。
在二值图像形态学中,结构元素是一个由0值和1值组成的矩阵。每一个结构元素有一个原点,结构元素中的原点指定待处理像素的位置。结构元素中的1值定义了结构元素的邻域,输出图像中对应原点的值建立在输入图像中相应像素及其邻域像素比较的基础上。在以下操作中,设Α表示二值图像,B表示结构元素,使用结构元素B对二值图像A进行操作。
2.2.1 膨胀
膨胀是将与物体接触的所有背景点合并到该物体中,使边界外部向外扩张的过程。通过膨胀,可以填充图像中的小孔及在图像边缘外的小凹陷部分。

2.2.2 腐蚀
腐蚀和膨胀是对偶操作。腐蚀是移除图像中目标边界的像素,使边界向内部收缩的过程。利用腐蚀操作,可以消除小且无意义的物体。

2.2.3 开运算

2.2.4 闭运算

2.3 实验仪器与软件
(1) PC计算机
(2) MatLab或opencv
(3) 实验所需要的图片
2.4 实验报告要求
描述实验的基本步骤,用数据和图片给出各个步骤中取得的实验结果和源代码,并进行必要的讨论,必须包括原始图像及其计算/处理后的图像。
2.5 实验内容及步骤
(1)图像膨胀
a)对包含矩形对象的二进制图像进行膨胀操作。
BW=zeros(9,10);
BW(4:6,4:7)=1;
imshow(BW,'notruesize')
se=strel('square',3);
BW2=imdilate(BW,se);
figure,imshow(BW2,'notruesize')b)改变上述结构元素类型(如:line, diamond, disk等),重新进行膨胀操作。
Line: BW=zeros(9,10);
BW(4:6,4:7)=1;
imshow(BW,'notruesize')
se=strel('line',3,3);
BW2=imdilate(BW,se);
figure,imshow(BW2,'notruesize')
(2)图像腐蚀
a) 对图像‘circbw.tif’(系统自带图像可以直接读取)进行腐蚀操作。
BW1=imread('circbw.tif');
se=strel('arbitrary',eye(5));
BW2=imerode(BW1,se);
imshow(BW1)
figure,imshow(BW2)
b) 对图像‘text.tif’进行腐蚀操作。我的MATLAB没有自带text.tif,我换成了其他
BW=imread('text.tif');
se=strel('line',11,90);
BW2=imerode(BW3,se);
imshow(BW)
figure,imshow(BW2)
(3)膨胀与腐蚀的综合使用
a) 从原始图像‘circbw.tif’中删除电流线,仅保留芯片对象。
方法一:先腐蚀(imerode),再膨胀(imdilate);
BW1=imread('circbw.tif');
imshow(BW1)
se=strel('rectangle',[40 30]); %选择适当大小的矩形结构元素
BW2=imerode(BW1,se); %先腐蚀,删除较细的直线
figure,imshow(BW2)
BW3=imdilate(BW2,se); %再膨胀,恢复矩形的大小
figure,imshow(BW3)

方法二:使用形态开启函数(imopen)。
BW1=imread('circbw.tif');
imshow(BW1)
se=strel('rectangle',[30,20]);
BW2=imopen(BW1,se); %开启操作
figure,imshow(BW2)b)改变结构元素的大小,重新进行开启操作,观察处理结果。
se=strel(‘rectangle’,[20 10]);
se=strel(‘rectangle’,[50 40]);c)置结构元素大小为[4 3],同时观察形态开启(imopen)与闭合(imclose)的效果,总结形态开启与闭合在图像处理中的作用。
I=imread('circbw.tif');
imshow(I)
se=strel('rectangle',[4 3]);
I1=imopen(I,se); %开启操作
I2=imclose(I,se); %闭合操作
figure,imshow(I1)
figure,imshow(I2)
(4)利用数学形态学函数bwmorph(BW,'skel',Inf),对下面二值图像的目标提取骨架,并分析骨架结构。其中,BW表示二值图像。


图片自提:计算机视觉实验一:图像基础处理资源-CSDN文库
% 读入二值图像(替换'your_binary_image.png'为实际图像文件名)
BW = imread('your_binary_image.png');% 提取骨架
skeleton = bwmorph(BW, 'skel', Inf);% 显示原始图像和骨架
figure;
subplot(1, 2, 1);
imshow(BW);
title('Original Binary Image');subplot(1, 2, 2);
imshow(skeleton);
title('Skeleton');% 分析骨架结构
% 可以进行一些骨架结构分析,如检测骨架中的交叉点和端点。
% 以下是一个示例来检测和可视化骨架的交叉点和端点:% 检测骨架的交叉点
branchpoints = bwmorph(skeleton, 'branchpoints');% 检测骨架的端点
endpoints = bwmorph(skeleton, 'endpoints');% 可视化交叉点和端点
[r_branch, c_branch] = find(branchpoints);
[r_end, c_end] = find(endpoints);% 显示骨架,交叉点和端点
figure;
imshow(skeleton);
hold on;% 交叉点用红色表示
plot(c_branch, r_branch, 'ro', 'MarkerSize', 10);% 端点用蓝色表示
plot(c_end, r_end, 'bo', 'MarkerSize', 10);title('Skeleton with Branchpoints and Endpoints');



3.实验参考图像

相关文章:

计算机视觉实验一:图像基础处理
1. 图像的直方图均衡 1.1 实验目的与要求 (1)理解直方图均衡的原理与作用; (2)掌握统计图像直方图的方法; (3)掌握图像直方图均衡的方法。 1.2 实验原理及知识点 直方图均衡化是通过灰度变换将一幅图象转换为另一幅均衡直方图,即在每个灰度级上都具有相同的象素…...

【WebApi】C# webapi 后端接收部分属性
在C#的Web API后端接收部分属性,可以使用[FromBody]特性配合JsonPatchDocument或者Delta来实现。这里提供一个使用JsonPatchDocument的示例。 首先,定义一个模型类:public class User public class User {public int Id {get; set; }...

Java 使用 Redis
Java 使用 Redis 1. 引言 Redis是一个开源的、基于内存的数据结构存储系统,可以用作数据库、缓存和消息中间件。它支持多种类型的数据结构,如字符串、哈希、列表、集合、有序集合等。由于Redis基于内存,其读写速度非常快,因此被广泛应用于需要高速缓存和实时通讯的场景。…...

【ONE·Linux || 高级IO(二)】
总言 主要内容:多路转接:epoll学习。 文章目录 总言5、多路转接:epoll5.1、相关概念与接口5.1.1、基本函数认识5.1.1.1、epoll_create5.1.1.2、epoll_ctl5.1.1.3、epoll_wait 5.1.2、epoll的工作原理5.1.2.1、准备工作(…...
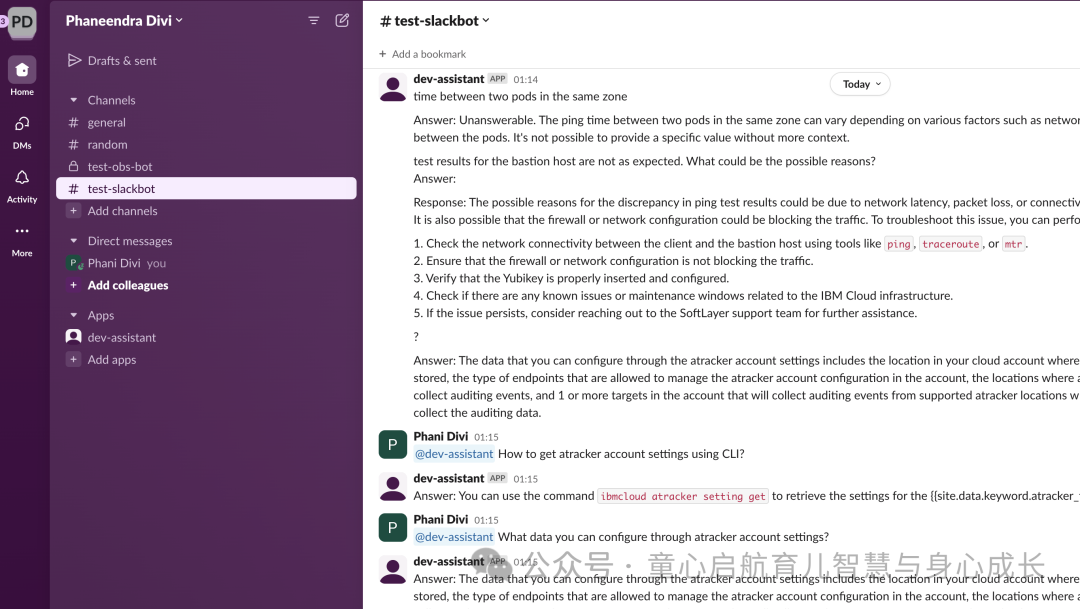
将 IBM WatsonX 数据与 Milvus 结合使用,构建用于知识检索的智能 Slack 机器人
在当今快节奏的工作环境中,快速轻松地访问信息对于保持生产力和效率至关重要。无论是在 Runbook 中查找特定说明,还是访问关键知识转移 (KT) 文档,快速检索相关信息的能力都可以产生重大影响。 本教程将指导您构建一个…...

2024 网鼎杯 CTF --- Crypto wp
文章目录 青龙组Crypto1Crypto2 白虎组Crypto1Crypto2 朱雀组Crypto2Crypto3part1part2part3part4 青龙组 Crypto1 题目: from Crypto.Util.number import * from secret import flagp getPrime(512) q getPrime(512) n p * q d getPrime(299) e inverse(d,…...

深度学习基础知识-损失函数
目录 1. 均方误差(Mean Squared Error, MSE) 2. 平均绝对误差(Mean Absolute Error, MAE) 3. Huber 损失 4. 交叉熵损失(Cross-Entropy Loss) 5. KL 散度(Kullback-Leibler Divergence&…...

《逆向记录》
这里写自定义目录标题 1.什么是vmp加密VMP加密的工作原理VMP加密的应用场景和优缺点实际应用案例 2.什么是ast混淆3.魔改算法总结 1.什么是vmp加密 VMP加密(Virtual Machine Protection)是一种软件保护技术,旨在通过虚拟化和加密技术来保…...

chatgpt3.5权重参数有多少MB;llama7B权重参数有多少MB
目录 chatgpt3.5权重参数有多少MB llama7B权重参数有多少MB chatgpt3.5权重参数有多少MB 关于ChatGPT 3.5的权重参数占用的存储空间大小,虽然直接给出具体的MB数值可能较为困难(因为这取决于多种因素,如参数表示的精度、是否进行了压缩等),但可以根据其参数量来估算一个…...

ST IoT Wireless 物联网与无线技术 研讨会
一、研讨会背景与目的 ◆ 意法半导体致力于提供可靠且经济实惠的无线连接解决方案,包含Wireless NFC Security & Esim等产品。 ◆ 将智能物体连接到互联网和云,或者从更广泛的意义上说,连接到物联网(IoT)。 ◆ 远程监控、配…...

PHP实现雪花算法生成唯一ID
引言 雪花算法是Twitter开源的分布式ID生成算法,可以产生64位的ID。其中第一位是固定的正数标识,41位用于存储时间戳,剩下的为机器ID和序列号。通过时间戳、机器ID和序列号的组合,确保每个ID都是唯一的。 PHP代码 1、定义雪花算…...

APP的设置页面,应该怎样尽可能减少用户的输入操作呢
一、引言 在当今数字化时代,移动应用程序(APP)已经成为人们生活中不可或缺的一部分。无论是社交娱乐、工作学习还是日常生活,我们都离不开各种 APP 的帮助。而 APP 的设置页面作为用户调整应用参数、个性化定制功能的重要入口&am…...

Node.js:内置模块
Node.js:内置模块 Node.jsfs模块读取文件写入文件__dirname path模块路径拼接文件名解析 http模块创建服务 Node.js 传统的JavaScript是运行在浏览器的,浏览器就是其运行环境。 浏览器提供了JavaScript的API,以及解析JavaScript的解析引擎&a…...

3. keil + vscode 进行stm32协同开发
1. 为什么使用vscode 主要还是界面友好,使用习惯问题,vscode 从前端,js, c/c, qt, 仓颉,rust都有很好插件的支持,并且有romote, wsl 等很多插件可以提高效率, 唯一的问题就是要使用插件进行环境…...

React 组件生命周期与 Hooks 简明指南
文章目录 一、类组件的生命周期方法1. 挂载阶段2. 更新阶段3. 卸载阶段 二、函数组件中的 Hooks1. useState2. useEffect3. useContext4. useReducer 结论 好的,我们来详细讲解一下 React 类组件的生命周期方法和函数组件中的钩子(hooks)。 …...

【springcloud】gateway网关的作用
目录 1. 说明2. 路由转发3. 负载均衡4. 安全认证与授权5. 熔断与降级6. 请求限流7. 监控与日志8. 过滤器功能 1. 说明 1.在Spring Cloud中,Gateway网关扮演着至关重要的角色。2.基于Spring Framework 5、Spring Boot和Project Reactor构建的API网关,专为…...

「C/C++」C++11 之<thread>多线程编程
✨博客主页何曾参静谧的博客📌文章专栏「C/C++」C/C++程序设计📚全部专栏「VS」Visual Studio「C/C++」C/C++程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasolid函数说明目…...

HTML前端页面设计静态网站-仿百度
浅浅分享一下前端作业,大佬轻喷~ <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>百度(伪)</title><style>body {margin: 0;padding: 0;}.top-bar {dis…...

百度SEO是否还有用?福州百度SEO专家林汉文为你深度解析
大家好,我是林汉文,一名专注于百度SEO优化的专家,最近有很多人问我:百度SEO还有用吗?在如今快速变化的数字营销环境中,这确实是一个值得探讨的问题。今天,我就来为大家详细分析百度SEO的现状&am…...
:使用Python基于WISP的多准则决策分析)
数学建模学习(134):使用Python基于WISP的多准则决策分析
WISP算法技术性文章 1. 算法介绍 WISP(Weighted Independent Set Problem)是一种优化算法,主要用于解决图论中的加权独立集问题。加权独立集问题是一个经典的组合优化问题,涉及从一个图中选择一个独立的顶点集,使得所选顶点的总权重最大。这个问题在计算机科学、运筹学、…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
LINUX编译vlc
下载 VideoLAN / VLC GitLab 选择最新的发布版本 准备 sudo apt install -y xcb bison sudo apt install -y autopoint sudo apt install -y autoconf automake libtool编译ffmpeg LINUX FFMPEG编译汇总(最简化)_底部的附件列表中】: ffmpeg - lzip…...

codeforces C. Cool Partition
目录 题目简述: 思路: 总代码: https://codeforces.com/contest/2117/problem/C 题目简述: 给定一个整数数组,现要求你对数组进行分割,但需满足条件:前一个子数组中的值必须在后一个子数组中…...

win11部署suna
参考链接 项目链接 沙盒链接 数据库链接 本文介绍 本文只为项目的辅助,手把手太麻烦 执行步骤 1.下载代码 git clone https://github.com/kortix-ai/suna.git cd suna2.配置环境(在Anaconda Prompt上执行) python setup.py3.运行代码 …...
