什么是贪心算法
贪心算法(Greedy Algorithm)是一种逐步构建解决方案的方法,在每一步选择中都作出局部最优的选择,希望最终能够获得全局最优解。贪心算法的核心思想是贪心选择性质,即每次选择当前看来最好的解,不考虑未来可能的影响。
贪心算法的特点
- 局部最优选择:贪心算法在每一步都只关心当前的最佳选择,而不关心全局的整体结构。这意味着它不做回溯或修改先前的选择。
- 不保证全局最优:贪心算法只能在某些特定问题(具有“最优子结构”特性)中才能得到全局最优解。在许多问题中,贪心算法只能获得近似解,无法保证是最优解。
- 效率较高:由于贪心算法不进行回溯和全局搜索,相比于其他方法(如动态规划),通常能够在较短时间内找到一个解,时间复杂度较低。
贪心算法的基本步骤
- 选择准则:在问题中确定每一步的选择标准,以保证每一步选择的最优性。
- 逐步构建解:按照贪心准则,每一步都选择当前最优的方案,并将该选择加入当前解中。
- 终止条件:当满足终止条件时,结束选择过程,得到最终解。
贪心算法的应用场景
贪心算法适合具有“贪心选择性质”和“最优子结构”的问题。以下是一些经典应用:
- 最小生成树(Minimum Spanning Tree):在图论中,Prim算法和Kruskal算法就是典型的贪心算法,用于构建最小生成树。
- 最短路径问题:在Dijkstra算法中,每一步选择当前到达某个节点的最短路径,最终得到从起点到其他节点的最短路径(仅适用于非负权重图)。
- 活动选择问题:在活动选择问题中,每次选择当前最早结束的活动,最终可以安排最多的活动。
- 背包问题(0-1背包问题的贪心解法):虽然经典的0-1背包问题无法通过贪心算法得到最优解,但分数背包问题可以用贪心算法解决,选择单位价值最高的物品。
贪心算法的优缺点
优点
- 简单直观:贪心算法的思想简单,每一步都选择当前看起来最优的解,易于理解和实现。
- 效率高:贪心算法通常只需遍历一遍数据,因此时间复杂度较低,效率较高。
缺点
- 不保证最优解:贪心算法不考虑全局情况,只关注当前的最优选择,可能导致最终解不是全局最优。
- 依赖问题特性:贪心算法只在特定问题中有效,只有具备“贪心选择性质”和“最优子结构”特性的问题才能用贪心算法求得最优解。
贪心算法的实例
例子:找零钱问题
假设你有面值为1元、5元、10元和20元的硬币,现在需要用尽量少的硬币组合凑出27元。
- 选择准则:每次选择面值最大的硬币且不超过剩余金额。
- 步骤:
- 选择一枚20元硬币,还剩下7元。
- 选择一枚5元硬币,还剩下2元。
- 选择两枚1元硬币,刚好凑成27元。
这种方式总共用了4枚硬币,即获得了最少硬币数的解。
不过,如果硬币面值不满足某些特性,贪心算法可能无法获得最优解。例如,在面值为1元、3元、4元的硬币中凑6元,贪心算法可能会选择4+1+1,得到3枚硬币的解,而不是最优解(2枚硬币,即3+3)。
总结
贪心算法是一种每一步都选择局部最优解的算法,在特定问题中能够有效且快速地找到解,但不保证全局最优。它在图论、贪心选择问题、动态规划等领域中有着广泛应用。
相关文章:

什么是贪心算法
贪心算法(Greedy Algorithm)是一种逐步构建解决方案的方法,在每一步选择中都作出局部最优的选择,希望最终能够获得全局最优解。贪心算法的核心思想是贪心选择性质,即每次选择当前看来最好的解,不考虑未来可…...

YOLOv6-4.0部分代码阅读笔记-effidehead_lite.py
effidehead_lite.py yolov6\models\heads\effidehead_lite.py 目录 effidehead_lite.py 1.所需的库和模块 2.class Detect(nn.Module): 3.def build_effidehead_layer(channels_list, num_anchors, num_classes, num_layers): 1.所需的库和模块 import torch import t…...
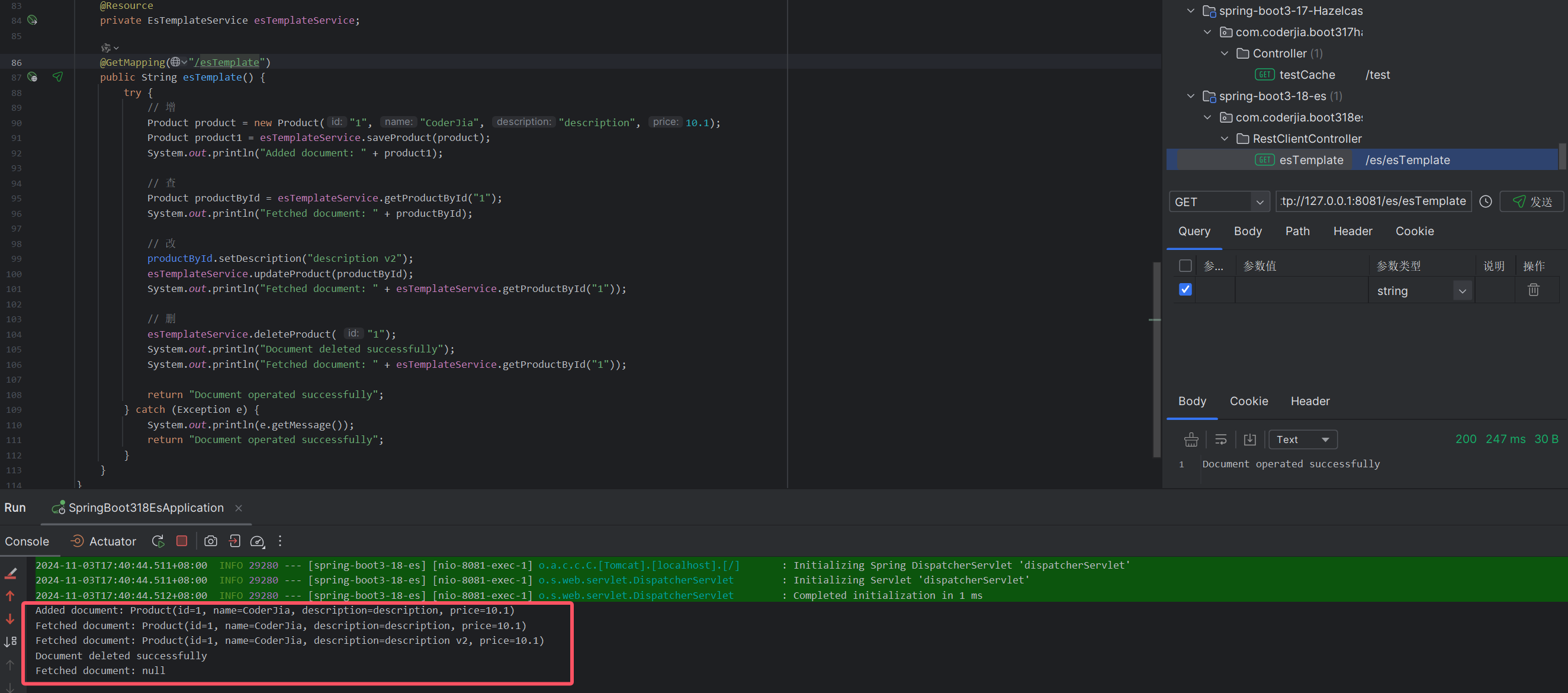
重学SpringBoot3-整合 Elasticsearch 8.x (一)客户端方式
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 这里写目录标题 1. 为什么选择 Elasticsearch?2. Spring Boot 3 和 Elasticsearch 8.x 的集成概述2.1 准备工作2.2 添加依赖 3. Elasticsearch 客户端配置方式…...

极简实现酷炫动效:Flutter隐式动画指南第三篇自定义Flutter隐式动画
目录 前言 一、TweenAnimationBuilder 二、使用TweenAnimationBuilder实现的一些动画效果 1.调整透明度的动画 2.稍微复杂点的组合动画 3.数字跳动的动画效果 前言 上两节博客分别介绍了Flutter中的隐式动画的基础知识以及使用隐式动画实现的一些动画效果。当系统提供的隐…...

无人机维护保养、部件修理更换技术详解
无人机作为一种精密的航空设备,其维护保养和部件修理更换是确保飞行安全、延长使用寿命的重要环节。以下是对无人机维护保养、部件修理更换技术的详细解析: 一、无人机维护保养技术 1. 基础构造理解: 熟悉无人机的基本构造,包括…...

xilinx vitis 更换硬件平台——ZYNQ学习笔记5
1、重新生成硬件信息 2、选择带有bit信息 3、设施路径和名字 4、打开更新硬件选项 5、选择新的硬件信息 6、打开系统工程界面 7、复位硬件信息 更新完毕...
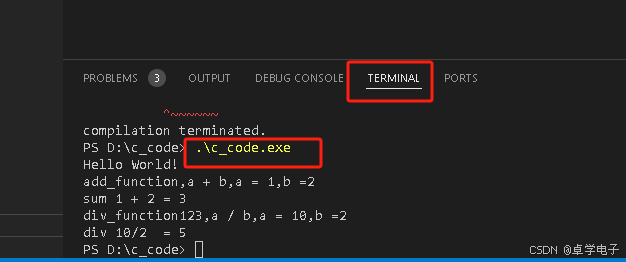
vscode makfile编译c程序
编译工具安装 为了在 Windows 上安装 GCC,您需要安装 MinGW-w64。 MinGW-w64 是一个开源项目,它为 Windows 系统提供了一个完整的 GCC 工具链,支持编译生成 32 位和 64 位的 Windows 应用程序。 1. 下载MinGW-w64源代码,如图点…...

【学术论文投稿】探索嵌入式硬件设计:揭秘智能设备的心脏
【IEEE出版】第六届国际科技创新学术交流大会暨通信、信息系统与软件工程学术会议(CISSE 2024)_艾思科蓝_学术一站式服务平台 更多学术会议论文投稿请看:https://ais.cn/u/nuyAF3 目录 引言 嵌入式系统简介 嵌入式硬件设计的组成部分 设…...

JavaScript 概述
### JavaScript 概述 JavaScript 是一种广泛使用的编程语言,它最初由 Netscape 公司的 Brendan Eich 在1995年创建,目的是为网页添加交互性。随着时间的发展,JavaScript 已经从一个简单的脚本语言演变成了一种功能强大的编程语言,…...

2024年10月个人工作生活总结
本文为 2024年10月工作生活总结。 研发编码 一个证书过期问题记录 某天,现场反馈某服务无法使用问题,经同事排查,是因为服务证书过期导致的。原来,证书的有效期设置为5年,这个月刚好到期。 虽然这个问题与自己无直接…...

uniapp ,微信小程序,滚动(下滑,上拉)到底部加载下一页内容
前言 小程序的内容基本都是滑动到底部加载下一页,这个一般都没有什么好用的组件来用,我看vant和uniapp的插件里最多只有个分页,没有滚动到底部加载下一页。再次做个记录。 效果预览 下滑到底部若是有下一页,则会自动加载下一页&…...

MySQL中的日志类型有哪些?binlog、redolog和undolog的作用和区别是什么?
简介: MySQL中有六种日志文件,分别是:重做日志(redo log)、回滚日志(undo log)、二进制日志(binlog)、错误日志(errorlog)、慢查询日志࿰…...

【uni-app】创建自定义模板
1. 步骤 打开自定义模板文件夹 在此文件夹下创建模板文件(注意后缀名) 重新点击“新建页面” 即可看到新建的模板 2. 注意事项 创建的模板必须文件类型对应(vue模板就创建*.vue文件, uvue模板就创建*.uvue文件)...

Cesium移动Primitive位置
与传统的Entity实体不同,Primitive作为一种自定义基本图元,几何形状、材质和其他属性均由使用者定义,在需要绘制大量静态几何图形的高效渲染场景中更为适用。 Primitive的移动涉及到矩阵变换,并不像Entity那样给它替换一个新的坐…...

安卓13默认连接wifi热点 android13默认连接wifi
总纲 android13 rom 开发总纲说明 文章目录 1.前言2.问题分析3.代码分析4.代码修改5.编译6.彩蛋1.前言 有时候我们需要让固件里面内置好,相关的wifi的ssid和密码,让固件起来就可以连接wifi,不用在手动操作。 2.问题分析 这个功能,使用普通的安卓代码就可以实现了。 3.代…...

parted 磁盘分区
目录 磁盘格式磁盘分区文件系统挂载使用扩展 - parted、fdisk、gdisk 区别 磁盘格式 parted /dev/vdcmklabel gpt # 设置磁盘格式为GPT p # 打印磁盘信息此时磁盘格式设置完成! 磁盘分区 开始分区: mkpart data_mysql # 分区名&…...

第三百零八节 Log4j教程 - Log4j日志到数据库
Log4j教程 - Log4j日志到数据库 我们可以使用log4j API通过使用org.apache.log4j.jdbc.JDBCAppender对象将信息记录到数据库中。 下表列出了JDBCAppender的配置属性。 属性描述bufferSize设置缓冲区大小。默认大小为1。driverJDBC驱动程序类。默认为sun.jdbc.odbc.JdbcOdbcDr…...

ai智能语音电销机器人可以做哪些事情?
AI智能语音电销机器人是结合人工智能技术进行自动化电话销售和客户互动的工具,能够完成一系列任务,有助于提升销售效果、优化客户体验和提高工作效率。以下是AI智能语音电销机器人可以做的一些主要事情: 1. 自动拨号 AI语音电销机器人可以自…...
CleanShot X - Mac(苹果电脑)专业截图录屏软件
CleanShot X 不仅提供了基础的截图功能,更内置了强大的图片编辑器,让你能轻松添加标注、形状、文本……以及将多个截图进行合并。 无论是为社交媒体制作图文,还是制作专业的产品 / 教程演示,CleanShot X 都能满足你的需求。 软件…...

Kafka 客户端工具使用分享【offsetexplorer】
前言: 前面我们使用 Spring Boot 继承 Kafka 完成了消息发送,有朋友会问 Kafka 有没有好用的客户端工具,RabbitMQ、RocketMQ 都有自己的管理端,那 Kafka 如何去查看发送出去的消息呢? 本篇我们就来分享一个好用的工具…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
