精华帖分享|缠论系列 -笔
本文来源于量化小论坛策略分享会板块精华帖,作者为吴奕萱,发布于2023年6月4日。
以下为精华帖正文:
01
笔
昨天讲了3根K线组合关系的完全分类,按照逻辑,其实我们会考虑是不是应该讲4根、5根K线的组合关系了。
精华帖分享 | 缠论系列
的确如此,在讲缠师的笔之前,我们来聊聊,为什么从3根K线之后,就是笔的出现,而不是更多根K线组合?
先来看看4根K线的组合关系完全分类,很容易得出,从高低点比较的情况的来看,是有4*2 = 8种情况的。
我们来比较下:
3根K线的情况下,转折最高点和最低点的位置出现在哪里是有迹可循的:
顶分型的最高点,肯定在第2根K线;
底分型的最低点,肯定在第2根K线;
4根K线的情况下,画图举个例子吧:
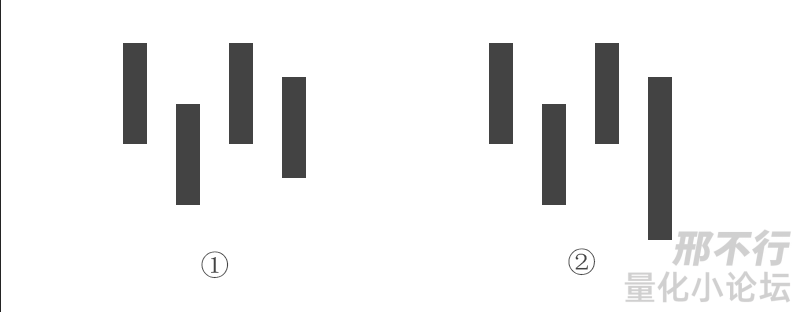
最低点在哪?可能在第二根,可能在第4根。
那么5根K线,6根K线,可能会更加犬牙交错,情况会更加复杂。
所以缠师忽略了这一些波动,工具用的就是笔!(这里的信息也会缺失)
当然笔的出现,原因肯定不在与此,这个后面聊到动力学的时候,还可以再分析一遍,聊到两者结合的时候还可以再分析一遍,我们这里仅仅从形态学处理的角度出发,讲了我的一点片面的观点。前面我尽量不讲没出现过的概念和解释。
到这里为止,我们来想想我们是怎么从分笔数据到笔的概念的,分笔数据 → 和成K线 → K线包含 → K线分型 → 笔,再这些最小的概念里面,我们还忽略了一个东西:缺口!
为什么之前没有讲缺口这个概念,是因为缺口,代表的东西有些复杂。
(缺口在不同的情况下,在形态学上都有不同的用法,但背后的原理又是动力学的东西,形式上要涉及到中枢,级别,所以在没有讲走势级别和动力学前,挺不好说的。)
这里简单一点,大部分的缺口,可以看成独立的1根虚拟K线,后面我们再详细说,缺口成K,缺口成笔,甚至成段的条件。(这一部分,成段是原文有出处的,成笔和成K是推理出来的)
下一篇,我们讲笔的定义。
02
笔的定义
网络上的笔概念杂七杂八的特别多,但原文中,只有两种,一种是老笔(严格笔),一种是新笔(宽松笔)。
老笔和旧笔定义的规则都是动力学原理,后面讲动力学的时候可以讨论一下。
在讲笔定义之前,还需要了解2个小学数学上的定义:结合律和交换律(牢记,后面时刻都要用!)
举个简单的例子:
结合律:a + b + c = (a + b) + c = a + (b + c) ;只要算子的位置没变,其运算顺序就不影响运算结果。
交换律:a + b = b + a ; 算子的位置改变,不影响运算结果。
K线本身具有时间序列的属性,两根K线是否能交换位置,还能保持原来的信息含量,显然是不能的。那么笔的定义也只符合结合律,而不符合交换律的。(牢记牢记)
严格笔的定义:
所谓笔,就是顶和底之间的其他波动,都可以忽略不算(65原文)。
两个相邻的顶和底之间构成一笔(65原文)。
注意:一定是相邻的顶和底,隔了几个就不是了(65原文)。
必须遵守结合律(原文)。
上升笔:底分型+上升K线+顶分型(65原文)
下降笔:顶分型+下降K线+底分型(65原文)
其实这个不太合适用上升K线和下降K线的说法,更合适的是独立K线(这两种K线都是一种组合关系,缠师实际是用独立K线,后文也有提到77课)。
上升笔(改):底分型+N根独立K线+顶分型,N>0
下降笔(改):顶分型+N根独立K线+底分型,N>0
在同一笔中,顶分型中最高那 K 线的区间至少要有一部分高于底分型中最低那 K 线的区间(77原文)。
如图(以上升笔为例)
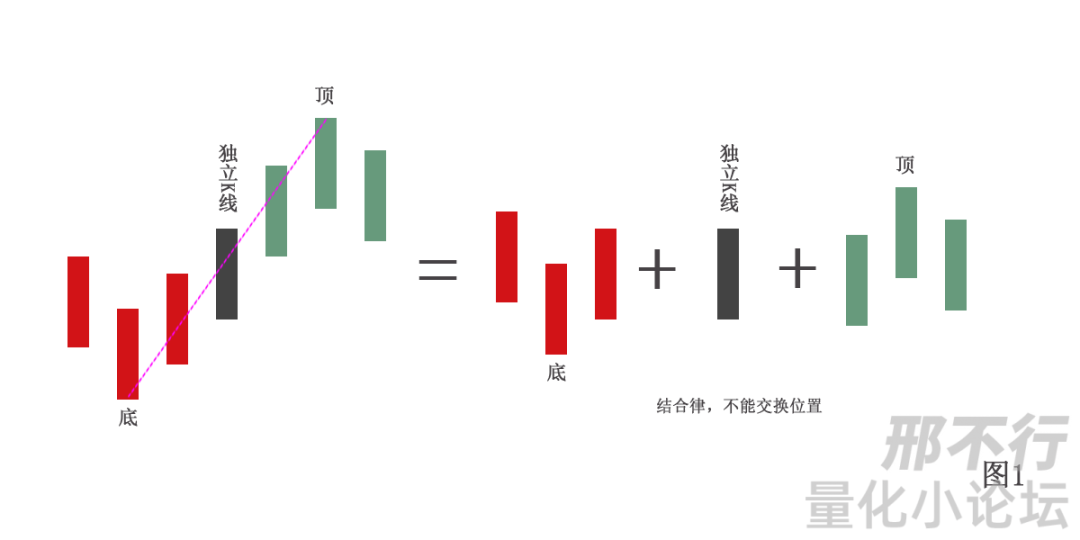
新笔定义:
顶分型和底分型经过包含关系处理后,不允许公用K线(81原文)。
顶分型的最高原始K线和底分型的最低原始K线间(不包含这两根),至少有3根K线(不考虑包含关系),即大于等于3根原始K线。(81原文)。
以底分型最小模型为例(顶分型的最小模型可以自行去画一下),如图:
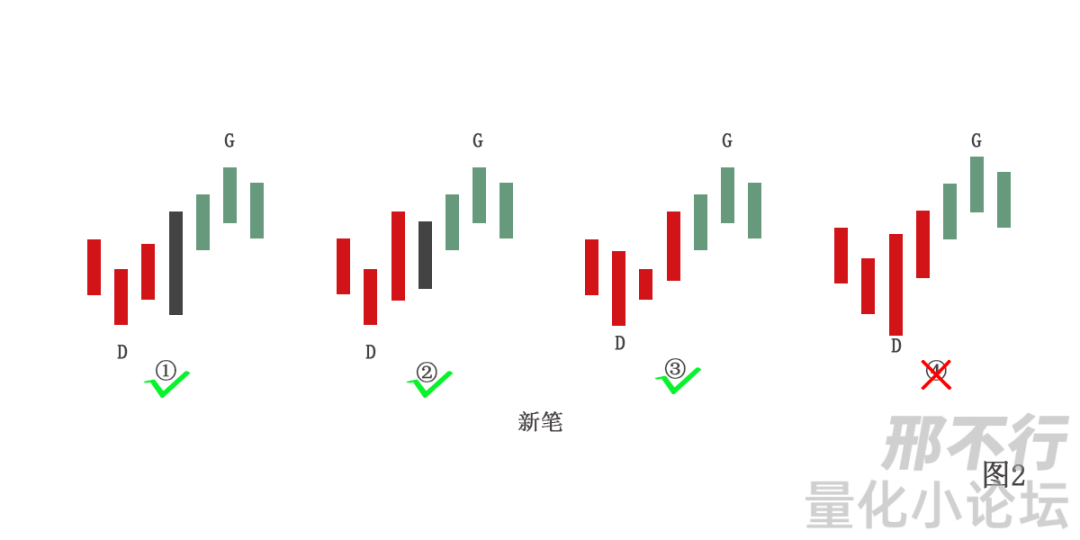
这里按照定义,1号2号3号是满足条件的,而4号是不满足条件的,原因是D和G之间不满足3根K条件。
按照完全分类的思想,这里还需要考虑一种情况,就是缺口,因为从笔开始,就要考虑到缺口因素了,那么有缺口的情况怎么算?
如图:
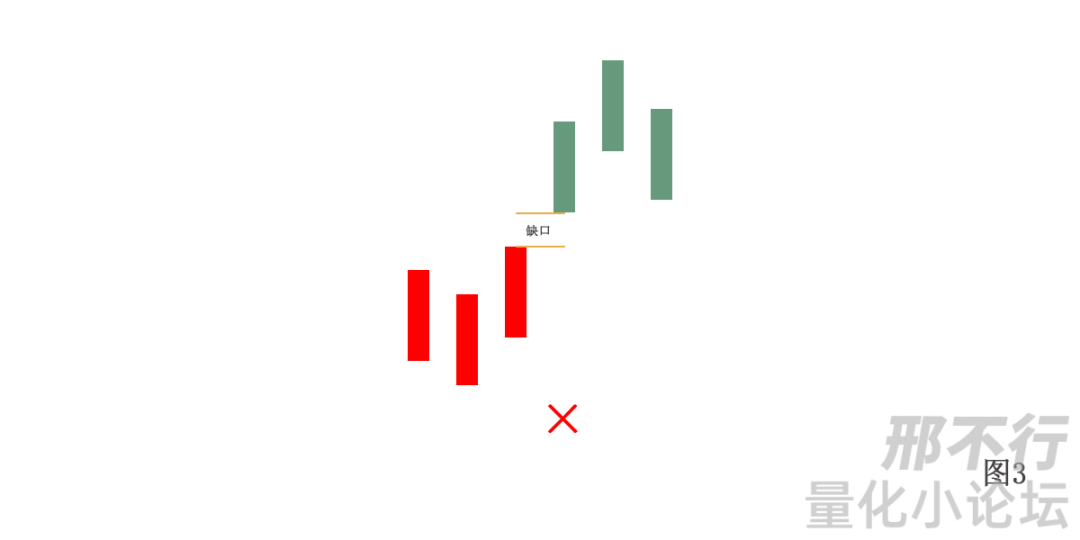
缠师是有在回复里面说过这个问题的,当时他讲的是不可以成立,原因是时间因素特别重要!(81回复)
但是原文中,缺口又有成段的论述,所以这里的不成立,只是一般状态。具体的成段成笔的条件,需要等到讲中枢,讲走势的时候再进行讨论。
所以,在不满足时间因素的时候,也就是K线根数的条件下,缺口一般是没有形态学意义的。如果满足了K线根数的条件下,一般情况,缺口在形态学中只是代表了一根普通的K线,只有在极为特殊的时候,缺口能成笔,成段。
那么新笔,老笔,用什么?
缠师的回复是,他一直用的都是老标准。
新笔和老笔的差别在哪里,从信息学角度,和实用主义的角度,或者别的角度,大家可以讨论下。
下一章,讲讲画笔的步骤。
03
笔的步骤
前文有一点忘记展开来详细说说了,就是“从分型到笔,必须是一顶一底”。
那么,两个顶或者底能不能构成一笔?
完全分类有两种情况:
在两个顶或底中间,有其他的顶和底;
在两个顶或底中间,没有其他的顶和底。
我尝试用图来表达下:
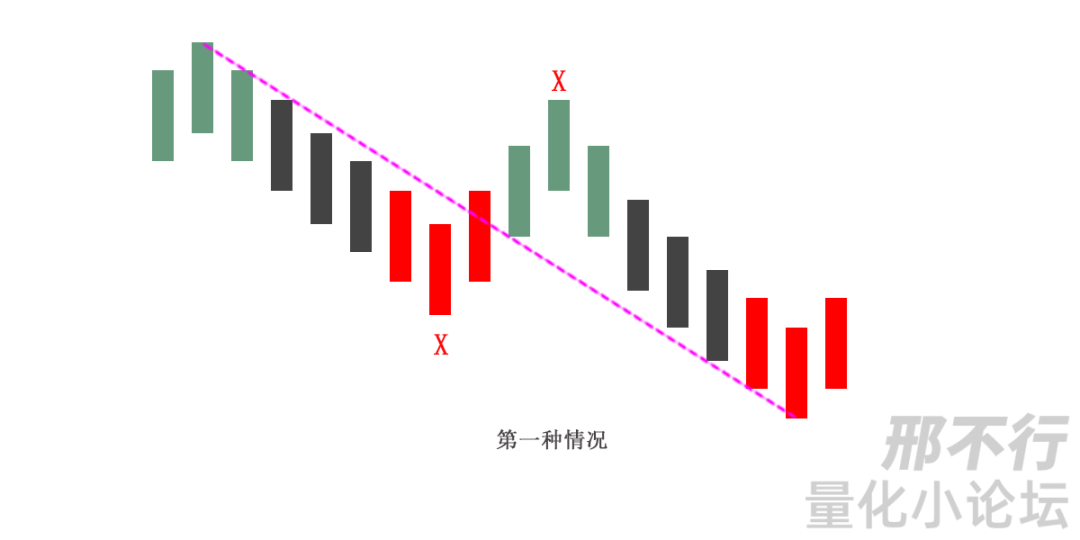
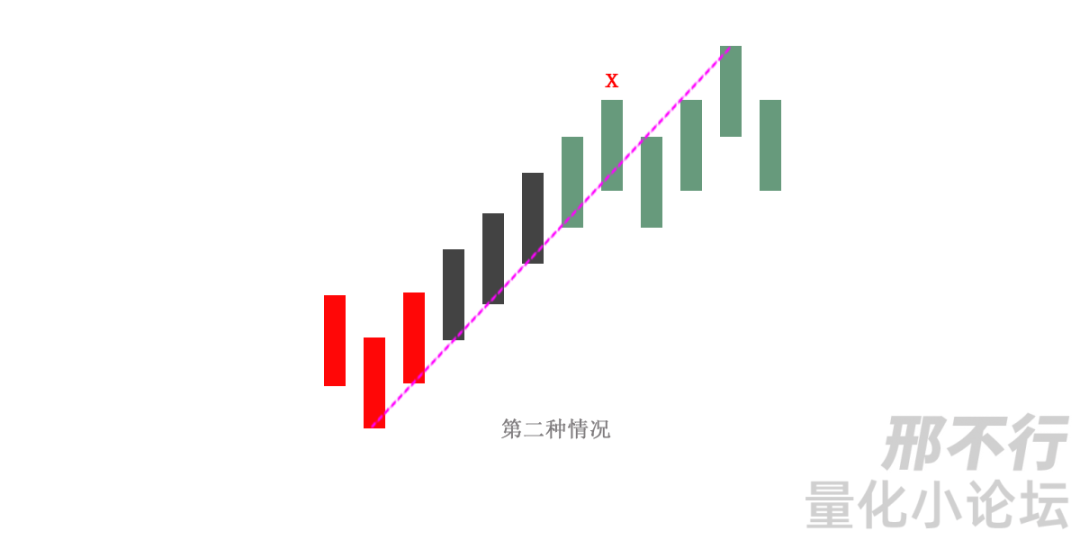
第一种情况,在两个顶或底中间有其他的顶和底,这种情况,只是把好几笔当成了一笔,所以只要继续用一顶一底的原则,自然可以解决;如上图中的两个绿色的顶分型,中间有一个底分型。
笔的定义清楚了之后,我们来聊聊该画笔的流程,这个对我们量化思路的整理很有效果。
缠师在原文中讲过一套画笔的方法,我这里先复现一下,然后再聊聊我的思路。
缠师画笔方法:
确定所有符合标准的分型。
相邻无共用K线;
如果前后两分型是同一性质的:
对于顶,前面的低于后面的,只保留后面的,前面那个可以 X 掉;
对于底,前面的高于后面的,只保留后面的,前面那个可以 X 掉;
不满足上面情况的,例如相等的,都可以先保留。
经过步骤2的处理后,余下的分型,如果相邻的是顶和底,那么这就可以划为一笔。如果相邻的性质一样,那么必然有前顶不低于后顶,前底不高于后底:
在连续的顶后,必须会出现新的底,把这连续的顶中最先一个,和这新出现的底连在一起,就是新的一笔,而中间的那些顶,都 X 掉;
在连续的底后,必须会出现新的顶,把这连续的底中最先一个,和这新出现的顶连在一起,就是新的一笔,而中间的那些底,都 X 掉。
如图:
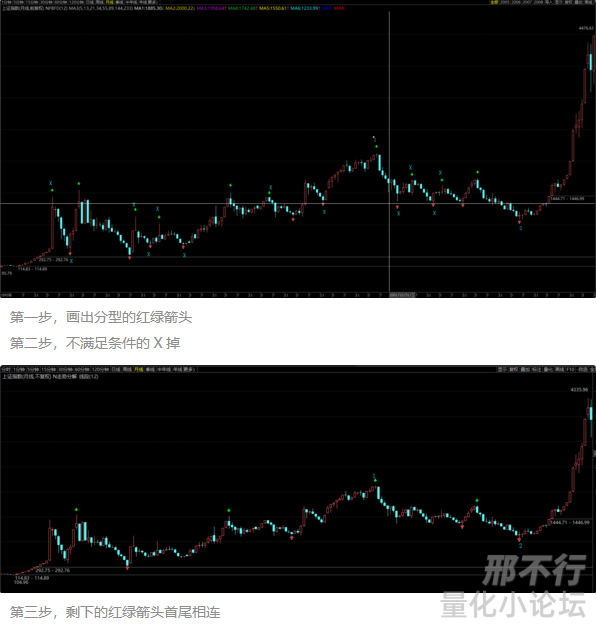
(大家仔细看,这个图里面有没有不符合操作的规则的顶底分型)
是不是,感觉很简单,但是实际操作下来,这里面有个小情况,然后缠师也有前后矛盾的地方。
先看图:
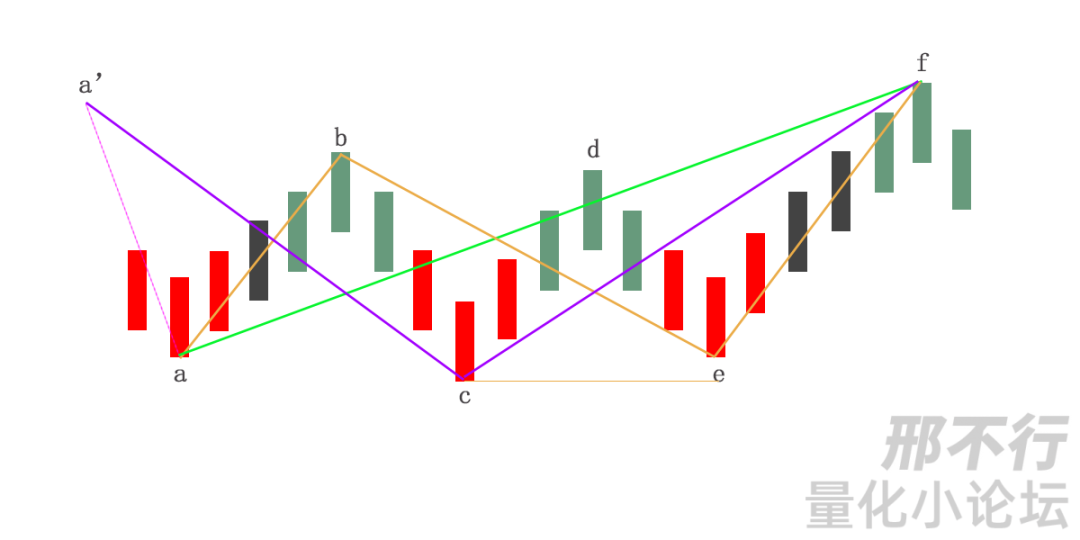
这张图,从a'到f这个笔该怎么来划分?
按照缠师的步骤,c、e这2个分型都是不符合标准的,这样说起来,应该是a'a,af这样的划分,如同图中的绿色笔。
那么问题来了,a点是比c点高的,而缠师有在61课的回复中有讲过,我贴下原文:
Q:一笔是否也有类似线段那样得三角形态或奔走形态?或者说,一笔之中的非顶、底 K 线是否允许超出顶底的范围呢?顶或底是否一定为一笔的最高点或最低点呢?
缠中说禅:一笔,是一顶一底,怎么会有三角形?顶和底,当然一定是那一笔的最高最低,如果不是,那里面一定不只一笔。
这句话:【当然一定是那一笔的最高最低】,但是图中c点是比a要低的。
ok,有问题!
后面,缠师又在77课的中有个回复,我引述一下:
Q:请问下图中的笔,是AD一笔呢?还是AB,BC,CD三笔呢?
缠中说禅:AB肯定不是一笔,BC也不是,至于AD是不是,这要看D后面的走势。
找笔,首先要找分型。A、D都满足分型的条件,但关键看D后面的分型是顶还是底,如果是顶,那么AD就是一笔。如果是底,那D肯定不是和A构成一笔的那个底。
附图:
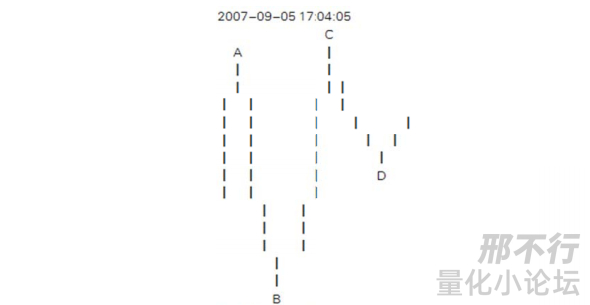
如果AD成一笔,那么这一笔的最低点在B,而不在D,和61课中的回复是矛盾的。
【注:当然这个图是有问题的,C比A高,所以连到A的这一笔,到C应该是延续,所以个人觉得,这个笔应该是到C一个上升笔,CD一个下降笔。】
【这里感谢下顾同学,因为以前CD这里我是不算笔的。】
如果按照71课的回复,那么我们上图的a'到f的划分,可以是按照黄色线的划分也是可以的。
还有个紫色的,大家看完,可以自行分析。
我们再来看看缠中说禅笔定理:
缠中说禅笔定理:任何的当下,在任何时间周期的 K 线图中,走势必然落在一确定的具有明确方向的笔当中(向上笔或向下笔),而在笔当中的位置,必然只有两种情况:
在分型构造中;
分型构造确认后延伸为笔的过程中。
根据这个定理,对于任何的当下走势,在任何一个时间周期里,我们都可以用两个变量构成的数组精确地定义当下的走势。
第一个变量,只有两个取值,1 代表向上的笔,-1 代表向下的笔;
第二个变量,只有两个取值,0 代表分型构造中,1 代表分型确认延伸为笔的过程中。
那么这两个变量,在完全分类下,只有4种情况:
(1,1) :代表着一个向上的笔在延伸之中;
(1,0) :代表向上的笔出现了顶分型结构的构造;
(-1,1):代表向下的笔在延伸中;
(-1,0):代表向下的笔出现底分型的构造。
如下图:
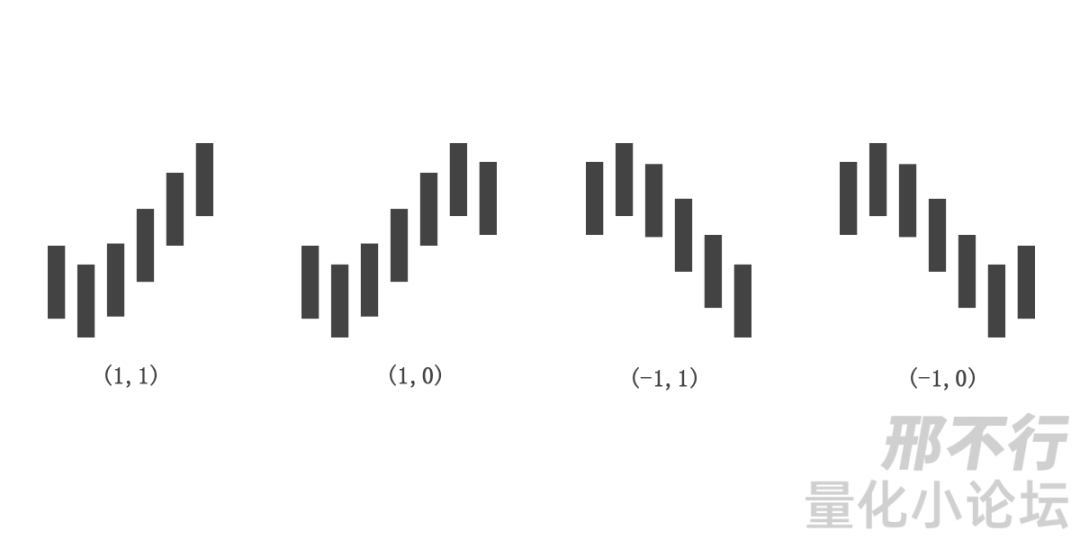
这里要注意的是分型构造和分型确认的区分:
分型构造:出现顶底分型后,一直到满足笔的最低数量K线(5根K线)出现前的状态都是分型构造的状态。
分型确认,是指分型构造完成后,在满足笔的最低数量K线之后,该分型就确认了。
如下图:
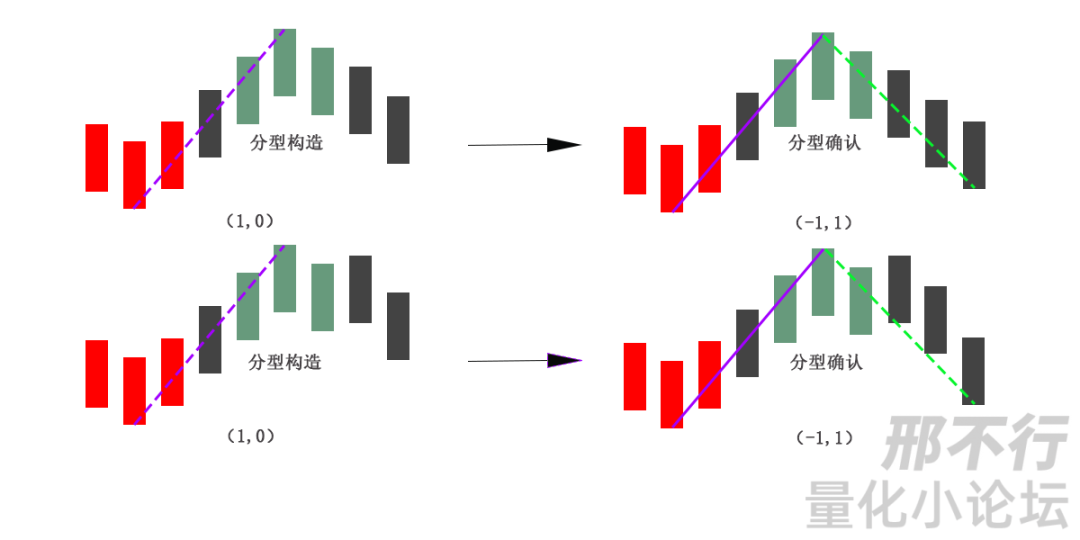
上图中:
1、所有的红色的底分型,都是已确认的状态,而左边的绿色的顶分型,都是在构造状态,右边的绿色顶分型就是确认的状态!
2、虚线表示延伸中的笔(因为分型构造没有完成),而实线表示完成的笔(分型已经确认,反向笔正在延伸)。
这四种状态也不是随便两两连接的,总共分为6种情况(完全分类):
(1,1) 连接 (1,0);
(-1,1) 连接 (-1,0);
(1,0) 连接 (1,1) ;
(1,0) 连接 (-1,1);
(-1,0) 连接 (-1,1);
(-1,0) 连接 (1,1) ;
如下图:
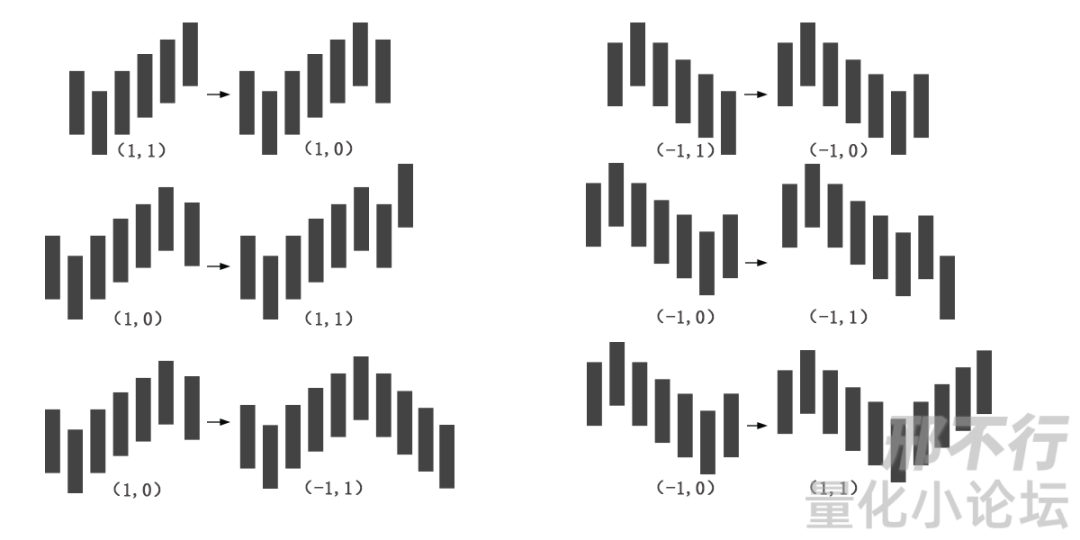
分型一旦确定,不可修改(这句话有原文);
笔的确定可以通过分型的构造和确认形成,这种方法是可以再当下去确认笔的状态的。
根据上述笔定理,讲讲我的画笔的流程:
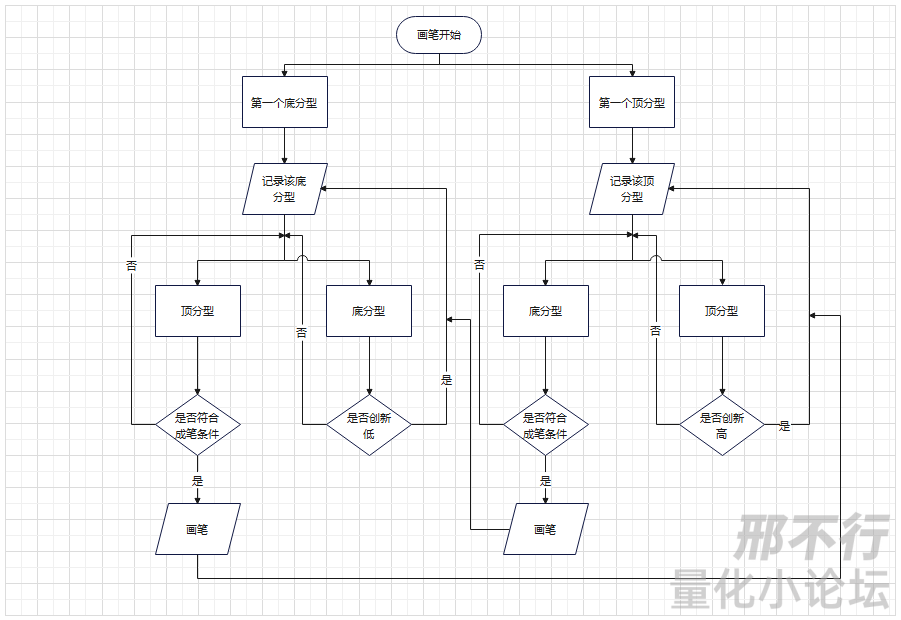
相关文章:

精华帖分享|缠论系列 -笔
本文来源于量化小论坛策略分享会板块精华帖,作者为吴奕萱,发布于2023年6月4日。 以下为精华帖正文: 01 笔 昨天讲了3根K线组合关系的完全分类,按照逻辑,其实我们会考虑是不是应该讲4根、5根K线的组合关系了。 精华帖…...

Java项目实战II基于Spring Boot的文理医院预约挂号系统的设计与实现(开发文档+数据库+源码)
目录 一、前言 二、技术介绍 三、系统实现 四、文档参考 五、核心代码 六、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者,专注于大学生项目实战开发、讲解和毕业答疑辅导。 一、前言 在医疗资源日益紧张的背景下࿰…...

NumPy Ndarray学习
1.NumPy Ndarray 对象简介 NumPy 最重要的特点是其 N 维数组对象 ndarray,它是一系列同类型数据的集合,以 0 下标为开始进行集合中元素的索引。ndarray 对象是用于存放同类型元素的多维数组。ndarray 中的每个元素在内存中都有相同存储大小的区域。 2.N…...

Browserslist 配置
Browserslist 是一个工具和规范,用于定义和共享支持的浏览器列表,以便在前端开发中管理不同工具的兼容性。这些工具可以包括 Babel、Autoprefixer、ESLint 等,它们都可以使用 Browserslist 提供的配置来确定应支持哪些浏览器及其版本。 主要…...

vue2中的v-bind相当于原生js的什么
在 Vue 2 中,v-bind 是一个指令,用于动态地将一个或多个属性绑定到 DOM 元素上。它相当于在原生 JavaScript 中直接操作 DOM 元素属性的方法。 v-bind 的基本用法 在 Vue 中,v-bind 可以这样使用: <!-- 绑定一个属性 -->…...

c语言-scanf函数的用法
文章目录 一、scanf是什么?二、通过scanf进行赋值scanf 输入一段带空格的句子, %[^\n] 格式字符串。 三、赋值忽略符 一、scanf是什么? 函数原型:int scanf ( const char * format, … ); scanf是一个格式输出库函数,…...

AI带货主播插件开发之商品推荐模块!
AI带货主播,作为新兴的人工智能技术应用领域,正逐渐改变着电商直播的格局,在这一领域,商品推荐模块是提升用户体验、增加销售额的关键一环。 本文将探讨AI带货主播插件的商品推荐模块开发,并分享五段关键的源代码&…...

使用Nginx作为反向代理和负载均衡器
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 使用Nginx作为反向代理和负载均衡器 引言 Nginx 简介 安装 Nginx Ubuntu CentOS 配置 Nginx 作为反向代理 配置 Nginx 作为负载…...

【数据结构二叉树】C非递归算法实现二叉树的先序、中序、后序遍历
引言: 遍历二叉树:指按某条搜索路径巡访二叉树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。 除了层次遍历外,二叉树有三个重要的遍历方法:先序遍历、中序遍历、后序遍历。 1、递归算法实现先序、中序、后…...

解决网盘资源搜索难题的利器——全面解析哎哟喂啊盘搜及其优秀推荐平台
海量的资源让我们的选择更加丰富,但同时也带来了资源搜索的诸多痛点。无论是寻找最新的影视资源、软件工具,还是各类学习资料,用户常常面临以下几个问题: 资源更新不及时:很多平台资源更新缓慢,用户难以第一时间获取最新内容。 搜索效率低下:关键词搜索不精准,导致需要翻阅大量…...

草料二维码:低成本高效率的访客管理解决方案
在当前的商业和政治环境中,企业和政府机构越来越重视安全保密措施,尤其是对外来人员的行踪记录和管理。访客管理已成为企业运营中不可或缺的一环,它不仅提升了安全性,还增强了效率和便捷性。然而,许多机构仍在使用传统…...

qt管理系统框架(好看界面、漂亮界面、好看的界面、漂亮的界面)
概述 最近一个项目用QT开发,然后找了美工帮设计了下界面。总算完工,后想一下干脆抽出一个基础框架,方便以后用。 功能 支持mysql、echarts。 支持加载动态权限菜单,轻松权限控制。 支持遮罩对话框、抽屉 支持开机启动动画界面 内…...
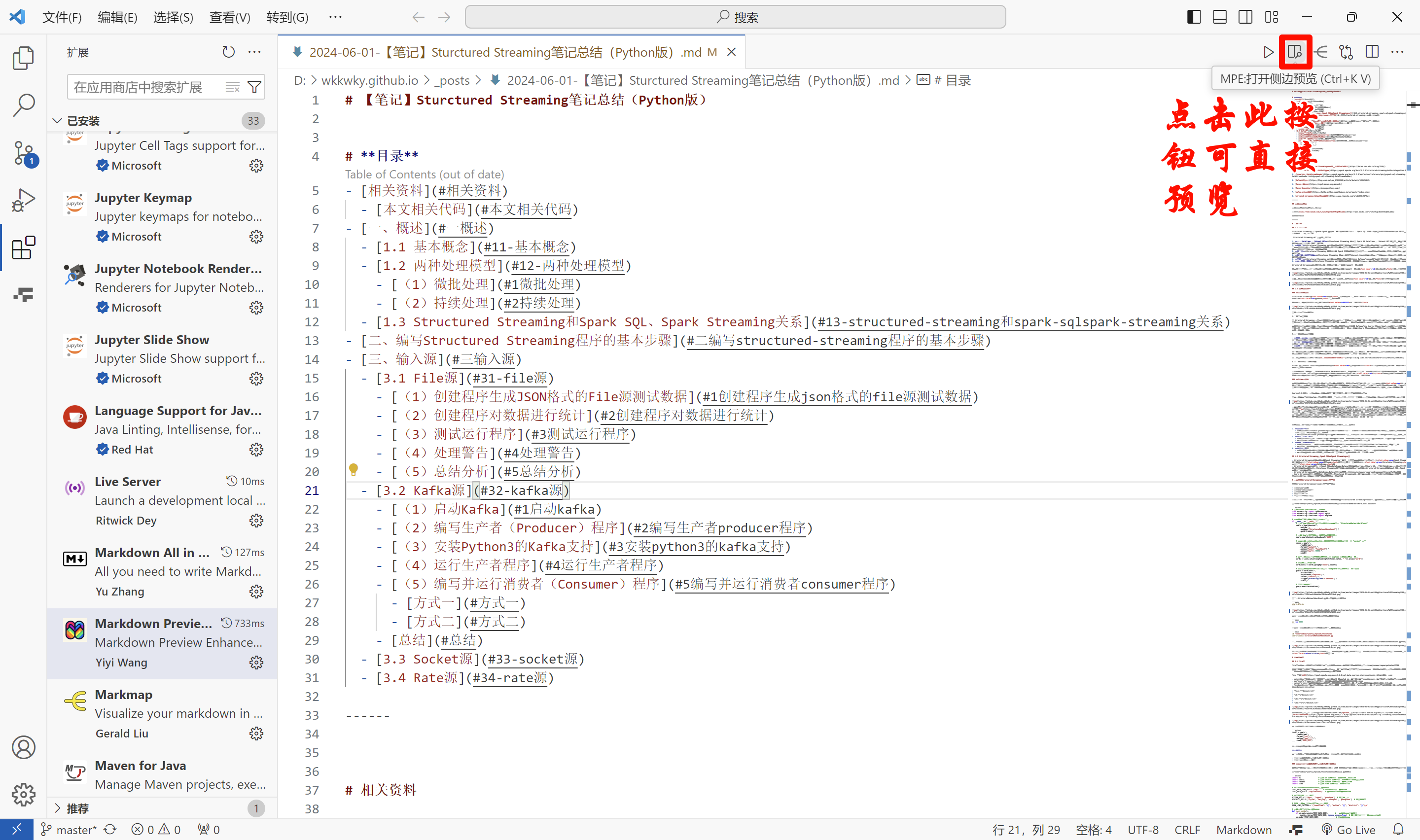
在VSCode中读取Markdown文件
在VSCode安装Markdown All in One或Markdown Preview Enhanced即可 插件Markdown All in One GitHub:https://github.com/yzhang-gh/vscode-markdown v3.6.2下载链接:https://marketplace.visualstudio.com/_apis/public/gallery/publishers/yzhang/vs…...

Linux rabbitmq客户端 SimpleAmqpClient 源码编译
SimpleAmqpClient的编译成库,加入到工程中 1、下载SimpleAmqpClient 源码: git克隆的路径为:https://github.com/alanxz/SimpleAmqpClient.git 下载压缩包路径:https://codeload.github.com/alanxz/SimpleAmqpClient/zip/maste…...

一台手机可以登录运营多少个TikTok账号?
很多TikTok内容创作者和商家通过运营多个账号来实现品牌曝光和产品销售,这种矩阵运营方式需要一定的技巧和设备成本,那么对于很多新手来说,一台手机可以登录和运营多少个TikTok账号呢? 一、运营TikTok账号的数量限制 TikTok的官…...

Python毕业设计选题:基于Hadoop的租房数据分析系统的设计与实现
开发语言:Python框架:flaskPython版本:python3.7.7数据库:mysql 5.7数据库工具:Navicat11开发软件:PyCharm 系统展示 系统首页 房屋信息详情 个人中心 管理员登录界面 管理员功能界面 用户管理界面 房屋信…...

k8s Service四层负载:服务端口暴露
在 Kubernetes 中,通过 Service 可以实现四层(L4)负载均衡,将流量分发至后端的 Pod。四层负载主要用于传输层(TCP/UDP),而不像七层负载均衡(HTTP/HTTPS)那样进行应用层的…...

QT 关于mousePressEvent无法过滤
QT 关于mousePressEvent无法过滤 bool Filter::eventFilter(QObject *watched, QEvent *event) {// 判断是不是点击事件if((event->type() QEvent::MouseButtonPress) || (event->type() QEvent::MouseButtonDblClick)){//打印一个全局变量static int globalVar 0;gl…...

【VScode】深度对比:Cursor与VScode(CodeMoss)工具,谁才是你的GPT编程最佳助手?
文章目录 一、Cursor的强大功能1.1 Cursor的主要特点1.2 Cursor的使用技巧 二、CodeMoss的功能2.1 CodeMoss的主要特点2.2 CodeMoss的使用技巧 三、Cursor与CodeMoss的对比分析3.1 功能对比3.2 性能对比 四、总结与展望 在科技迅猛发展的今天,AI编程工具如雨后春笋般…...

大数据计算里的-Runtime Filter
文章目录 Runtime Filter示例 Runtime Filter 从纸面意义来看,就是程序在运行时,根据实际的数据去进行一些过滤操作。这和静态的规则优化不同,静态优化不考虑实现的数据的分布。 示例 select a.* ,b.* a join b on a.idb.id假设一下数据…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
