【小白学机器学习31】 大数定律,中心极限定理,标准正态分布与概率的使用
目录
1 正态分布相关的2个相关定理
1.1 大数定律:(证明了)分布的稳定性
1.2 中心极限定理:(证明了)分布的收敛性
2 使用标准差和概率的2种思路
2.1 标准正态分布的曲线
2.2 两种使用方式
2.3 第1种:按整数倍标准差δ 作为标准使用
2.3.1 比如3δ原则 /6西格玛管理
2.3.2 还有LCL, UCL管理
2.2 第2种:按比较整的概率如95%对应的标准差使用
3 应用举例1
4 应用举例2:造成误差的原因不是样本数占总体的比例,而是样本的绝对数量!
关于正态分布,具体应用
1 正态分布相关的2个相关定理
1.1 大数定律:(证明了)分布的稳定性
- 大量试验结果稳定性
- 频率的稳定性,
- 伯努利大数定律:样本数多n变大,某个事件发生的频度 =单次试验内发生的概率
- 泊松大数定律: 样本数多n变大,样本平均值估计 =总体平均值
1.2 中心极限定理:(证明了)分布的收敛性
- 分布的收敛性
- 随机变量(如多次取样的均值)会逐渐符合某一分布:正态分布
- 二项分布的极限分布是正态分布
- 无论一组变量独立同分布,不管本身符合什么分布,但是有u和 δ^2。这组变量的样本平均数(多次抽样的平均数分分布)就服从 u和 δ^2/N的正态分布
2 使用标准差和概率的2种思路
2.1 标准正态分布的曲线
- 标准正态分布曲线,曲线下的面积可以表示概率
- 曲线上的每个点,都是Xi值的标准值
- 标准值=xi-u/sd

2.2 两种使用方式
- 我们根据不同的需要,确定了我们使用 2δ 还是2.58δ
- 如果有可能,我们使用其他标准的δ 都有可能,关键是根据需求来
- 当我们需要以整数δ为标准来看概率时,选择 δ,2δ,3δ等
- 当我们需要以比较整的概率时比如95%,99%时,比如做假设检验的适合,选择 1.96δ,2.58δ等
2.3 第1种:按整数倍标准差δ 作为标准使用
按照 -3δ,-2δ,-1δ,1δ,2δ,3δ 这样的整数倍δ来划分区间
- 3δ,49.8%,99.99%
- 2.58δ,49.5%,99%
- 2δ,47.7%,95.45%
- 1.96δ,47.5%,95%
- δ,34.1%,68.5%
- -δ,34.1%,68.5%
- -1.96δ,47.5%,95%
- -2δ,47.7%,95.45%
- -2.58δ,49.5%,99%
- -3δ,49.8%,99.99%
2.3.1 比如3δ原则 /6西格玛管理
- 标准正态分布与概率,3δ原则
- 不同的标准差δ对应不同的概率
- 按照几倍δ,去找对应的概率,68.5%,95.45%,99.99%等
2.3.2 还有LCL, UCL管理
- LCL“Low control limit 一般对应-3δ
- UCL:UP control limit 一般对应+3δ
2.2 第2种:按比较整的概率如95%对应的标准差使用
按概率 90% 95% 99%等比较整的概率去划分标准正态分布的区间
- 3δ,49.8%,99.99%
- 2.58δ,49.5%,99%
- 2δ,47.7%,95.45%
- 1.96δ,47.5%,95%
- δ,34.1%,68.5%
- -δ,34.1%,68.5%
- -1.96δ,47.5%,95%
- -2δ,47.7%,95.45%
- -2.58δ,49.5%,99%
- -3δ,49.8%,99.99%
3 应用举例1
- 使用样本均值 + 总体的标准差,去估计 总体均值的范围
- 使用样本均值 + 总体的标准差(样本标准差),去估计 总体均值的范围
我们如果只有1个样本,少数样本,虽然不能直接推算总体样本,但是可以这么估计范围。
比如在95%区间内
总体均值-1.96*标准差/sqrt(n) <= 样本平均值<=总体均值-1.96*标准差/sqrt(n)
因此
总体平均值<=样本平均值+1.96*标准差/sqrt(n)
总体平均值>=样本平均值-1.96*标准差/sqrt(n)当样本数量n一直增大后
总体平均值<=样本平均值+1.96*标准差/sqrt(n)=样本平均值+0
总体平均值>=样本平均值-1.96*标准差/sqrt(n) =样本平均值-0
总体平均值=样本平均值如果范围从95%→99%后,形象的看为什么置信区间变大了
总体平均值<=样本平均值+2.58 *标准差/sqrt(n)
总体平均值>=样本平均值-2.58 *标准差/sqrt(n)
范围变大,95%-99%,也就是置信区间变大了。而拒绝的空间α就很小了。这个计算实际存在理论上的问题。但是实际上我们容易得到样本均值,但很难得到总体标准差,而如果用样本的标准差去替代总体的,也是个办法,因为样本方差的分母从N改为(N-1)=总体方差,所以还是可以行得通的,但是肯定是有误差的。
4 应用举例2:造成误差的原因不是样本数占总体的比例,而是样本的绝对数量!
- 一个更奇怪的公式
- 95%时
- 样本p-1.96*sqrt((N-n)/(N-1)*p*(1-p)/n) <总体P< 样本p+1.96*sqrt((N-n)/(N-1)*p*(1-p)/n)
- 而(N-n)/(N-1) 样本数量n比较小时,趋近于1,故意忽略
- 样本p-1.96*sqrt(p*(1-p)/n) <总体P< 样本p+1.96*sqrt(p*(1-p)/n)
- 造成误差的原因
- 不是样本数占总体的比例,而是样本的绝对数量!
- 反常识!
相关文章:

【小白学机器学习31】 大数定律,中心极限定理,标准正态分布与概率的使用
目录 1 正态分布相关的2个相关定理 1.1 大数定律:(证明了)分布的稳定性 1.2 中心极限定理:(证明了)分布的收敛性 2 使用标准差和概率的2种思路 2.1 标准正态分布的曲线 2.2 两种使用方式 2.3 第1种:按整数倍标准差δ 作为标准使用 2.…...

Go语言基础语法
一、创建工程 说明: (1)go.mod文件是go项目依赖管理文件,相当于前端的package.json,也就是Java项目中的Maven的pom.xml。 二、打印数据到控制台 (1)引入fmt (2)使用fmt…...

CSS层叠/CSS变量和!important的使用
layer components {:root {--theme: red;font-family: serif !important;} } CSS Layers CSS Layers 是一种用于管理和组织样式规则的新机制。它允许开发者定义不同的样式层,以便更好地控制样式的优先级和覆盖关系。通过使用 layer 规则,开发者可以将样…...

提升工作效率的小众神器
🤖宝子们,今天我要给大家分享五款超实用的小众工作软件,让你的工作事半功倍!😎 🌟亿可达 - 自动化办公神器 亿可达是一款自动化办公工具,无需编程知识就能搭建出各种自动化工作流程。界面清新…...

【Python+Pycharm】2024-Python安装配置教程
【PythonPycharm】2024-Python安装配置教程 一、下载装 Python 1、进入Python官网首页,下载最新的Python版本 Download Python | Python.org 选择对应版本下载 安装 测试安装情况 python如果安装失败 在系统环境变量添加安装路径 where pythonwin7安装路径添加…...

systemverilog中clocking的用法
文章目录 1.clocking简介2.clocking实例分析3.重点分析(1)bus定义是不是随便取名的(2)输入输出的定义原则是什么(3)到底如何消除了竞争和冒险(4)没用到的信号如何处理(5&…...

【Python开发】大模型应用开发项目整理
不知不觉已经入职3个月了,同事很好,工作充实,学到了很多东西,大大小小的需求也实现了接近20个。负责2个主要component,数据抓取和利用GenAI做数据提取。 1 背景 提取新闻中事件关键信息,比如人名ÿ…...

Redis 的使⽤和原理
第一章:初识 Redis 1.1盛赞 Redis Redis 是⼀种基于键值对(key-value)的 NoSQL 数据库,与很多键值对数据库不同的是,Redis 中的值可以是由 string(字符串)、hash(哈希)、list&…...

前端学Java
一:语法 1、注解 注解(Annotation)是Java中的一种特殊类型的语法,它可以被用来为代码提供元数据。元数据是关于数据的数据,注解可以用于类、方法、变量等的描述与标记。 理解注解可以从以下几个方面入手:…...

VR游戏:多人社交将是VR的下一个风口
第一部分:创业笔记 1. 市场趋势 从单机游戏转向多人互动体验:随着技术的进步,VR游戏正从单机模式向多人互动体验转变。代表作品如Rec Room、Phasmophobia、Among Us和Breachers等,这些游戏的成功证明了多人互动模式的巨大潜力。…...
的不同)
Docker与虚拟机(VM)的不同
Docker与虚拟机(VM)在实现的原理上存在显著的不同,主要体现在以下几个方面: 一、基础原理 Docker 利用Linux内核的特性,如容器(containers)、命名空间(namespaces)和控制…...

Pr 视频效果:透视
效果面板/视频效果/透视 Video Effects/Perspective Adobe Premiere Pro 的视频效果中,透视 Perspective效果组主要用于在二维平面的视频剪辑中模拟三维空间的透视效果。 通过调整这些效果,可以改变图像的视角、添加阴影、创造立体感,增强画面…...

C 语言标准库 - <limit.h>
简介 <limits.h> 是 C 标准库中的一个头文件,定义了各种数据类型的限制。这些宏提供了有关整数类型(char、short、int、long 和 long long 等)和其他数据类型的最大值和最小值的信息。 这些限制指定了变量不能存储任何超出这些限制的…...

Python | Leetcode Python题解之第519题随机翻转矩阵
题目: 题解: class Solution:def __init__(self, m: int, n: int):self.m mself.n nself.total m * nself.map {}def flip(self) -> List[int]:x random.randint(0, self.total - 1)self.total - 1# 查找位置 x 对应的映射idx self.map.get(x,…...

大数据新视界 -- 大数据大厂之提升 Impala 查询效率:索引优化的秘籍大揭秘(上)(3/30)
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...

【AI工作流】FastGPT - 深入解析FastGPT工作流编排:从基础到高级应用的全面指南
文章目录 一、工作流编排概述二、FastGPT的节点类型1. 基础功能插件(1) 文本输出(2) 功能调用(3) 工具(4) 外部调用(5) 其他 2. 系统插件3. 团队插件 三、工作流中的流向结语 在当今快速发展的人工智能领域,工作流编排的能力已成为提升用户体验和应用效率的关键因素…...

VS+Qt解决提升控件后,包含头文件格式不对问题处理
一、前言 VSQt 提升控件后,在uic目录下会生成ui相关的初始化文件,对于提升的控件头文件包含的格式为#include<> 而非 #include “ ” 导致无法找到头文件。如果手动修改为 #include “ ”相当麻烦,甚至每次编译都要修改一遍,…...

opencv - py_imgproc - py_filtering filtering 过滤-卷积平滑
文章目录 平滑图像目标2D 卷积(图像过滤)图像模糊(图像平滑)1. 平均2. 高斯模糊3. 中值模糊4. 双边滤波 其他资源 平滑图像 目标 学习: 使用各种低通滤波器模糊图像将定制滤波器应用于图像(2D 卷积&…...
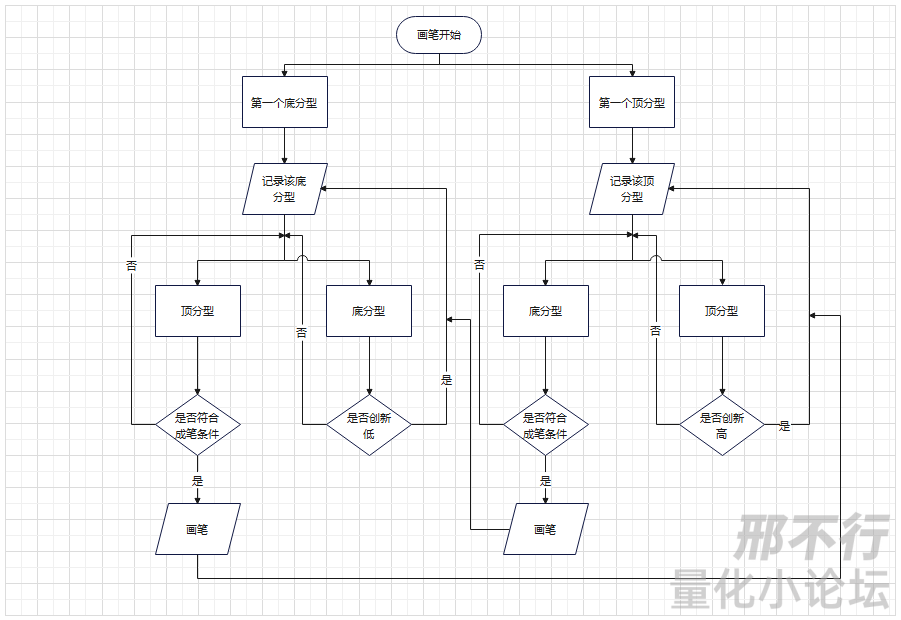
精华帖分享|缠论系列 -笔
本文来源于量化小论坛策略分享会板块精华帖,作者为吴奕萱,发布于2023年6月4日。 以下为精华帖正文: 01 笔 昨天讲了3根K线组合关系的完全分类,按照逻辑,其实我们会考虑是不是应该讲4根、5根K线的组合关系了。 精华帖…...

Java项目实战II基于Spring Boot的文理医院预约挂号系统的设计与实现(开发文档+数据库+源码)
目录 一、前言 二、技术介绍 三、系统实现 四、文档参考 五、核心代码 六、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者,专注于大学生项目实战开发、讲解和毕业答疑辅导。 一、前言 在医疗资源日益紧张的背景下࿰…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...
