算法:图的相关算法
图的相关算法
- 1. 图的遍历算法
- 1.1 深度优先搜索
- 1.2 广度优先搜索
- 2. 最小生成树求解算法
- 普里姆(Prim)算法
- 克鲁斯卡尔(Kruskal)算法
- 3. 拓扑排序
- 4. 最短路径算法
1. 图的遍历算法
图的遍历是指从某个顶点出发,沿着某条搜索路径对图中的所有顶点进行访问且只访问次的过程。
图的遍历算法是求解图的连通性问题、拓扑排序及求关键路径等算法的基础。
图的遍历要比树的遍历复杂得多。因为图的任一个结点都可能与其余顶点相邻接,所以在访问了某个顶点之后,可能沿着某路径又回到该结点上,为了避免对顶点进行重复访问,在图的遍历过程中必须记下每个已访问过的顶点。深度优先搜索和广度优先搜索是两种遍历图的基本方法。
1.1 深度优先搜索
类似树的先根遍历,在第一次经过一个顶点时就进行访问操作。遍历步骤如下:
- 设置搜索指针 p,使p指向顶点。
- 访问p所指顶点,并使p指向与其相邻接的且尚未被访问过的顶点。
- 若p所指顶点存在,则重复步骤(2),否则执行步骤(4)。
- 沿着刚才访问的次序和方向回溯到一个尚有邻接顶点且未被访问过的顶点,并使p指向这个未被访问的顶点,然后重复步骤(2),直到所有的顶点均被访问为止。
int visited[MaxN] = {0}; //调佣遍历算法前设置所有的顶点都被访问过
void Dfs(Graph G, int i)
{EdgeNode *t; int j;printf("%d",i); //访问序号为i的顶点visited[i] = 1; //序号为i的顶点已被访问过t = G.Vertices[i].firstarc; //取顶点i的第一个邻接顶点while(t!=NULL){ //检查所有与顶点i相邻接的顶点j=t->adjvex; //顶点j为顶点i的一个邻接顶点if(visited[j]==0) //若顶点j未被访问则从顶点j出发进行深度优先搜索Dfs(G,j);t=t->nextarc; //取顶点i的下一个邻接顶点}
}
1.2 广度优先搜索
图:广度优先搜索
图的广度优先搜索方法为:从图中的某个顶点v出发,在访问了之后依次访问v的各个未被访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问,直到图中所有已被访问的顶点的邻接点都被访问到。若此时还有未被访问的顶点,则另选图中的一个未被访问的顶点作为起点,重复上述过程,直到图中所有的顶点都被访问到为止。
广度优先遍历图的特点是尽可能先进行横向搜索,即最先访问的顶点的邻接点也先被访问。为此,引入队列来保存已访问过的顶点序列,即每当一个顶点被访问后,就将其放入队列中,当队头顶点出队时,就访问其未被访问的邻接点并令这些邻接顶点入队。
void Bfs(Graph G)
{EdgeNode *t; int i,j,k;int visited[MaxN]={0}; //调用遍历算法前设置所有的顶点都没有被访问过initQueue(Q); //创建一个空队列for(i=0;i<G.Vnum;i++){if(!visited[i]){ //顶点i未被访问过enQueue(Q,i);printf("%d",i);visited[i]=1; //访问顶点i并设置已访问标志while(!isEmpty(Q)){ //若队列不空,则继续取顶点进行广度优先搜索deQueue(Q,k);t=G.Vertices[k].firstarc;for(;t;t=t->nextarc){ //检查所有与顶点K相邻接的顶点j=t->adjvex; //顶点j是顶点k的一个邻接顶点if(visited[j]==0){ //若顶点j未被访问过,将j加入队列enQUeue(Q,j);printf("%d",j); //访问序号为j的顶点并设置已访问标志visited[j]=1;}}}}}
}
2. 最小生成树求解算法

生成树:设图G=(V,E)是个连通图,如果其子图是一棵包含G的所有顶点的树,则该子图称为G的生成树。
对于有n个顶点的连通图,至少有 n-1 条边,而生成树中恰好有 n-1条边,所以连通图的生成树是该图的极小连通子图。若在图的生成树中任意加一条边,则必然形成回路。
图的生成树不是唯一的。对于非连通图而言,每个联通分量中的顶点集和遍历时走过的边集一起构成若干棵生成树,把它们称为非连通图的生成树森林。
最小生成树:对于连通网来说,边是带权值的,生成树的各边也带权值,于是就把生成树各边的权值总和称为生成树的权,把权值最小的生成树称为最小生成树。求解最小生成树有许多实际的应用。普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法是两种常用的求解最小生成树算法。
普里姆(Prim)算法

克鲁斯卡尔(Kruskal)算法


3. 拓扑排序
在工程领域,一个大的工程项目通常被划分为许多较小的子工程(称为活动),当这些子工程都完成时,整个工程也就完成了。若以顶点表示活动,用有向边表示活动之间的优先关系,则称这样的有向图为以顶点表示活动的网(Activity On Vertex network,AOV 网)。在有向网中若从顶点 v i v_i vi到顶点 v j v_j vj有一条有向路径,则顶点 v i v_i vi是 v j v_j vj的前驱,顶点 v j v_j vj是 v i v_i vi的后继。若 < v i , v j > <v_i,v_j> <vi,vj>是网中的一条弧,则顶点 v i v_i vi是 v j v_j vj的直接前驱,顶点 v j v_j vj是 v i v_i vi的直接后继。AOV 网中的弧表示了活动之间的优先关系,也可以说是一种活动进行时的制约关系。
在 AOV 网中不应出现有向环、回路若存在的话,则意味着某项活动必须以自身任务的完成为先决条件,显然这是荒谬的。因此,若要检测一个工程划分后是否可行,首先就应检查对应的AOV 网是否存在回路。检测的方法是对其 AOV 网进行拓扑排序。

对一个有向图进行拓扑排序的结果会有两种情况:
- 一种是所有顶点已输出,此时整个拓扑排序完成,说明网中不存在回路;
- 另一种是尚有未输出的顶点,剩余的顶点均有前驱顶点,表明网中存在回路,拓扑排序无法进行下去。
4. 最短路径算法
狄克斯特拉算法
相关文章:

算法:图的相关算法
图的相关算法 1. 图的遍历算法1.1 深度优先搜索1.2 广度优先搜索 2. 最小生成树求解算法普里姆(Prim)算法克鲁斯卡尔(Kruskal)算法 3. 拓扑排序4. 最短路径算法 1. 图的遍历算法 图的遍历是指从某个顶点出发,沿着某条搜索路径对图中的所有顶点进行访问且只访问次的…...

django的models使用介绍。
from django.db import modelsfrom utils.models import CommonModel# Create your models here. class User(CommonModel):#用户数据模型username models.CharField(用户名,max_length32, uniqueTrue)password models.CharField(密码,max_length256)nickname models.CharFi…...

【分布式技术】分布式事务深入理解
文章目录 概述产生原因关键点 分布式事务解决方案3PC3PC的三个阶段:3PC相比于2PC的改进:3PC的缺点: TCCTCC事务的三个阶段:TCC事务的设计原则:TCC事务的适用场景:TCC事务的优缺点:如何解决TCC模…...

力扣hot100-->hash表/map
hash表/map 1. 1. 两数之和 简单 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。 …...

基于redis实现延迟队列
Redis实现延时队列 延时队列里装的主要是延时任务,用延时队列来维护延时任务的执行时间。 1、延时队列有哪些使用情景? 1、如果请求加锁没加成功 可以将这个请求扔到延时队列里,延后处理。 2、业务中有延时任务的需要 比如说࿰…...

PHP微信小程序共享充电桩系统设计与实现计算机毕业设计源代码作品和开题报告
博主介绍:黄菊华老师《Vue.js入门与商城开发实战》《微信小程序商城开发》图书作者,CSDN博客专家,在线教育专家,CSDN钻石讲师;专注大学生毕业设计教育、辅导。 所有项目都配有从入门到精通的基础知识视频课程ÿ…...

【网络面试篇】TCP与UDP类
目录 一、综述 1. TCP与UDP的概念 2. 特点 3. 区别 4. 对应的使用场景 二、补充 1. 基础概念 (1)面向连接 (2)可靠的 (3)字节流 2. 相关问题 (1)TCP 和 UDP 可以同时绑定…...
Windows转Mac过渡指南
最近由于工作原因开始使用mac电脑,说实话刚拿到手的时候,window党表示真的用不惯。坚持用一下午之后,发现真的yyds,这篇文章说说mac电脑的基本入门指南。 1. 不会使用mac的触摸板,接上鼠标发现滚轮和windows是反的。 …...

LeetCode100之盛最多水的容器(11)--Java
1.问题描述 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量 注意 你不能倾斜容器 示例1 输入&…...

【VMware】使用笔记
一、安装 win11支持16.2以上版本,其他版本不兼容 安装参考: 二、设置 1、蓝屏设置 参考:win11打开VMware虚拟机蓝屏解决_win11vmware蓝屏-CSDN博客 2、VMwareTool配置 第一步:移除“open-vm-tools” sudo apt-get autoremo…...

<项目代码>YOLOv8 猫狗识别<目标检测>
YOLOv8是一种单阶段(one-stage)检测算法,它将目标检测问题转化为一个回归问题,能够在一次前向传播过程中同时完成目标的分类和定位任务。相较于两阶段检测算法(如Faster R-CNN),YOLOv8具有更高的…...
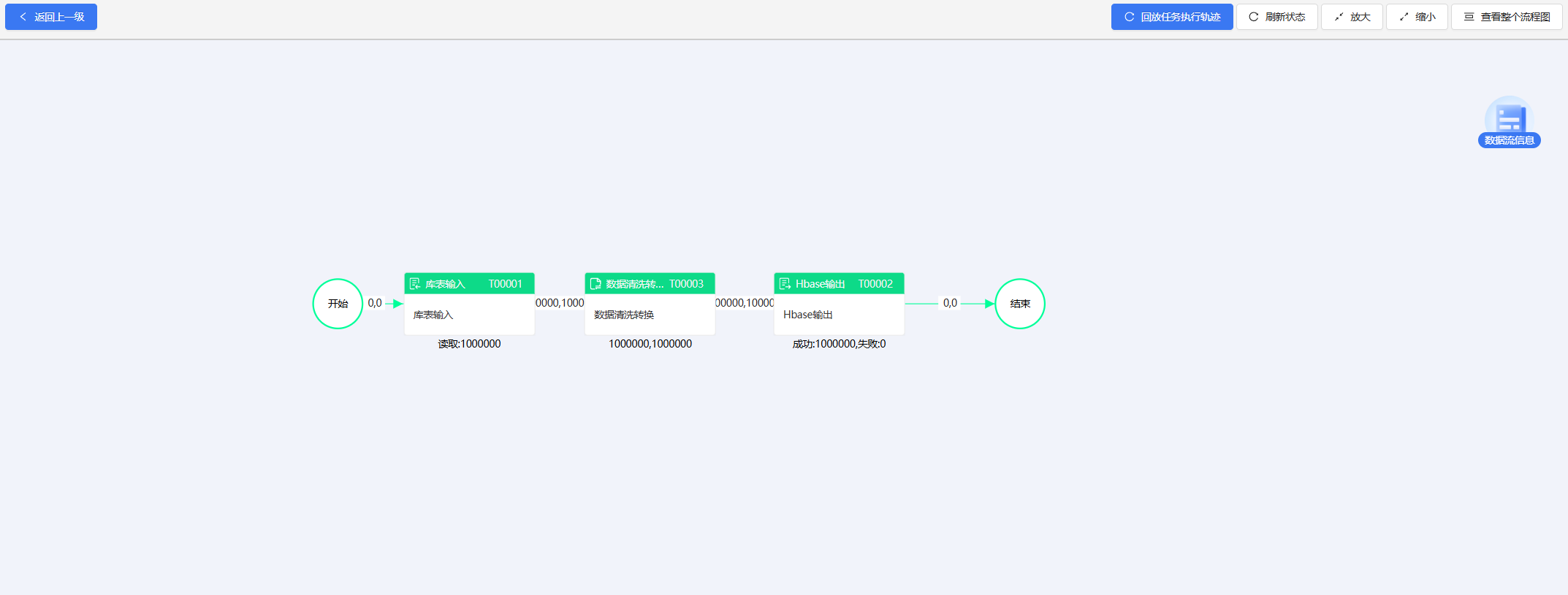
存储数据库的传输效率提升-ETLCloud结合HBASE
一、大数据存储数据库–HBASE HBase,作为一个开源的分布式列存储数据库,基于Google的Bigtable设计而成,专为处理大规模结构化数据而优化。使用HBase打造大数据解决方案的好处主要包括:高可扩展性,能够处理PB级的数据&…...

HO-XGBoost河马算法优化极限梯度提升树多变量回归预测(Matlab)
HO-XGBoost河马算法优化极限梯度提升树多变量回归预测(Matlab) 目录 HO-XGBoost河马算法优化极限梯度提升树多变量回归预测(Matlab)预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Matlab实现HO-XGBoost多变量回归预测&…...

【Hive sql面试题】找出连续活跃3天及以上的用户
表数据如下: 要求:求出连续活跃三天及以上的用户 建表语句和插入数据如下: create table t_useractive(uid string,dt string );insert into t_useractive values(A,2023-10-01 10:10:20),(A,2023-10-02 10:10:20),(A,2023-10-03 10:16…...

Linux curl命令下载显示时间/速度/大小
命令: curl -# -O --compressed -w "大小: %{size_download} bytes\n时间: %{time_total} seconds\n速度: %{speed_download} B/s\n" 下载URL链接。 例子: curl -# -O --compressed -w "大小: %{size_download} bytes\n时间: %{time_to…...
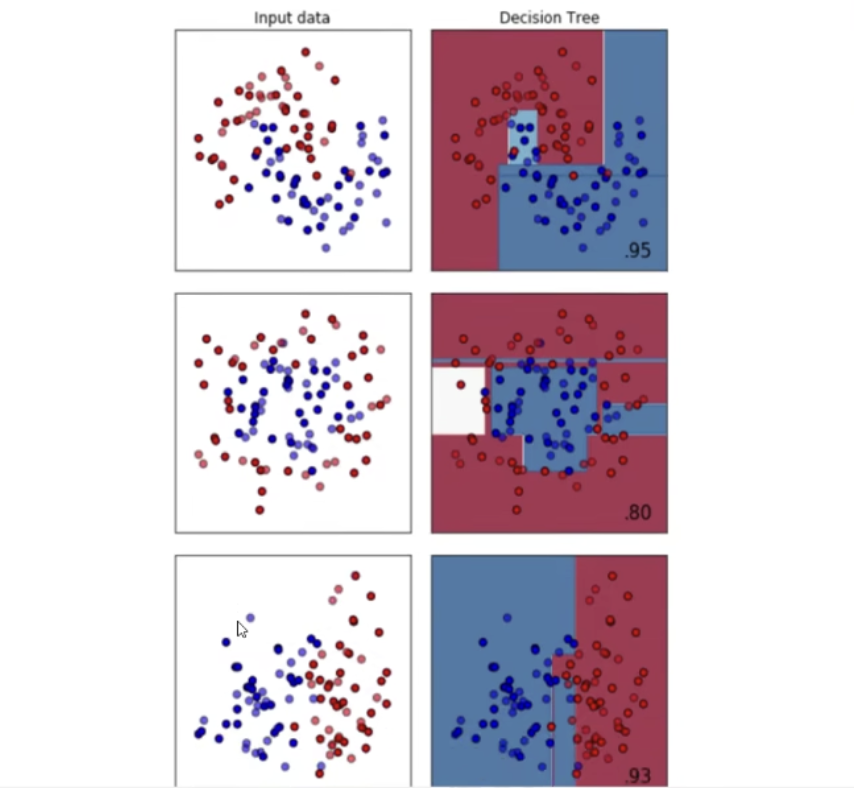
sklearn|机器学习:决策树(一)
文章目录 sklearn|机器学习:决策树(一)(一)概述(二)实战1. 环境配置2. sklearn 中的决策树(1)模块 sklearn.tree(2)sklearn 基本建模流…...

Rust中三种方式使用环境变量
环境变量是存储在操作系统中的一组键值对。它们用于存储系统和其他应用程序所需的配置信息。本文我们将探索如何在Rust中使用标准库以及dotenv crate来处理环境变量。 环境变量 环境变量提供了一种灵活的方式来配置应用程序,而无需直接在源代码中硬编码配置值。这…...

搭建支持国密GmSSL的Nginx环境
准备 1、服务器准备:本文搭建使用的服务器是CentOS 7.6 2、安装包准备:需要GmSSL、国密Nginx,可通过互联网下载或者从 https://download.csdn.net/download/m0_46665077/89936158 下载国密GmSSL安装包和国密Nginx安装包。 服务器安装依赖包…...
Docker部署Portainer CE结合内网穿透实现容器的可视化管理与远程访问
文章目录 前言1. 本地安装Docker2. 本地部署Portainer CE3. 公网远程访问本地Portainer-CE3.1 内网穿透工具安装3.2 创建远程连接公网地址4. 固定Portainer CE公网地址前言 本篇文章介绍如何在Ubuntu中使用docker本地部署Portainer CE可视化管理工具,并结合cpolar实现公网远程…...

不适合的学习方法
文章目录 不适合的学习方法1. 纯粹死记硬背2. 过度依赖单一资料3. 线性学习4. 被动学习5. 一次性学习6. 忽视实践7. 缺乏目标导向8. 过度依赖技术9. 忽视个人学习风格10. 过于频繁的切换 结论 以下是关于不适合的学习方法的更详细描述,包括额外的内容和相关公式&…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
