AcWing 1073 树的中心 树形dp (详解)
这道题目非常有新意,在过去,我们通常先访问子节点去更新父节点的状态,但是这道题我们还需要从父节点去更新子节点。
我们可以想象为向上和向下两个方向,我们任取一点,先向下走,再回来更新上面的点,这样我们就能得出向下的最长距离和次长距离,同时记录最长距离是走哪个点获得的。
然后我们再次深搜,对每个点用这个点去更新他所有子节点,因为他的子节点的最大向上值就是他的最大向上值或者向下最长距离或者次长距离加上这两点间的距离。
代码
#include <bits/stdc++.h>using namespace std;const int N = 100010, INF = 0x3f3f3f3f;int n, res = INF;int h[N], e[N], ne[N], w[N], idx;int d1[N], d2[N], s[N], up[N];void add(int a, int b, int c)
{e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}void dfs1(int u, int f)
{for (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (j == f) continue;dfs1(j, u);if (d1[j] + w[i] >= d1[u]){s[u] = j;d2[u] = d1[u];d1[u] = d1[j] + w[i];}else if (d1[j] + w[i] >= d2[u]){d2[u] = d1[j] + w[i];}}
}void dfs2(int u, int f)
{for (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (j == f) continue;if (s[u] == j) up[j] = w[i] + max(up[u], d2[u]);else up[j] = w[i] + max(up[u], d1[u]);dfs2(j, u);}
}int main()
{cin >> n;memset(h, -1, sizeof h);for (int i = 1; i < n; i ++ ){int a, b, c;cin >> a >> b >> c;add(a, b, c), add(b, a, c);}dfs1(1, -1);dfs2(1, -1);for (int i = 1; i <= n; i ++ ) res = min(res, max(up[i], d1[i]));cout << res << endl;return 0;
}相关文章:
)
AcWing 1073 树的中心 树形dp (详解)
这道题目非常有新意,在过去,我们通常先访问子节点去更新父节点的状态,但是这道题我们还需要从父节点去更新子节点。 我们可以想象为向上和向下两个方向,我们任取一点,先向下走,再回来更新上面的点…...

modelscope下载Qwen2.5 72B 模型方法
conda create -n modelscope python=3.10 conda activate modelscopepip install modelscope执行这个python代码: from modelscope.hub.snapshot_download import snapshot_download# 下载模型到当前路径 model_dir = snapshot_download(...
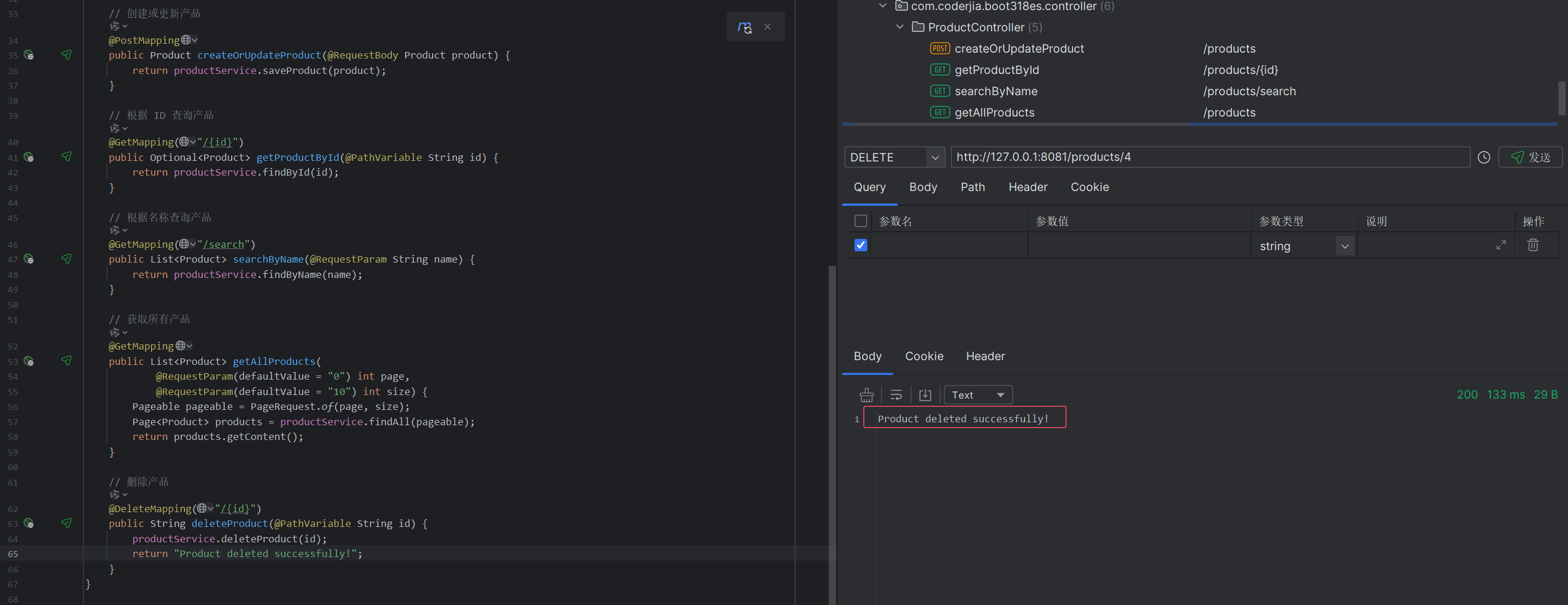
重学SpringBoot3-整合 Elasticsearch 8.x (二)使用Repository
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 整合 Elasticsearch 8.x (二)使用Repository 1. 环境准备1.1 项目依赖1.2 Elasticsearch 配置 2. 使用Repository的基本步骤2.1 创建实体类2.2 创…...

为什么说模拟电路的难点就在开通过程和关断过程?难在什么地方?
模拟电路中开通过程和关断过程之所以困难,主要有以下几个方面的原因: 1. 瞬态响应特性复杂 - 在开通和关断瞬间,电路中的电流和电压会发生快速变化,产生复杂的瞬态响应。这些瞬态响应可能包含过冲、下冲、振铃等现象,…...

CubeIDE BUG-project‘hello‘has no explict encoding set hello
projecthellohas no explict encoding set hello 解决方法: 点击红色处注册账号后登录,删除原本文件后重新生成即可。...

在线PDF转图片网站
https://www.ilovepdf.com/download/qgxkmbzgxt6yb3s8l9f7fc3q9606hq0bfh4b33mnrf3p7tp8l0d4qy386b5dxqwjbhq7j3j4tp20m4dnb89wA9jjw25br1gtAw42l0m1sq047nvld4qqrm8kzjplkAhw9458p4wjgbmn08g49l23c1khsggdx4A7z3m9xh19mgzdlllyA6r1/52 在线excel转图片 https://www.zamzar.c…...

ps和top的区别
时间上的区别: ps是静态查看进程而top是动态持续监控进程 功能上的区别 ps只是查看进程,top还可以监视系统性能,如平均负载,cpu和内存的消耗 ps 常用格式:ps -ef (ef简洁aux详细 System V风格和BSD 风格) | grep P…...

自动驾驶上市潮中,会诞生下一个“英伟达”吗?
站上科技创新潮头的企业总是备受资本青睐。20世纪开始,从IT到互联网,IBM、英特尔、微软、苹果等各大科技巨头,你方唱罢我登场。 近几年,人工智能成为资本市场新传奇故事的孕育之地。今年10月,英伟达市值首度突破3.5万…...

CSS 计数器:深入解析与高级应用
CSS 计数器:深入解析与高级应用 CSS 计数器是前端开发中一个强大但经常被忽视的功能。它们允许开发者创建和管理自定义的计数序列,这在处理复杂文档结构时尤其有用。本文将深入探讨 CSS 计数器的原理、用法,并展示一些高级应用示例。 什么是…...

【真题笔记】15年系统架构设计师要点总结
【真题笔记】15年系统架构设计师要点总结 分布式数据库中各种透明RAID 5IPv6 IPv4电子商务系统项目配置管理IPO图(输入加工输出图)桥接模式的UML图面向对象设计原则软件测试 在15年真题练习中,对错题模棱两可的考点进行重点记录与内容延申。…...
)
斗破C++编程入门系列之三十九:多态性:纯虚函数和抽象类(四星斗师)
斗破C目录: 斗破C编程入门系列之前言(斗之气三段) 斗破C编程入门系列之二:Qt的使用介绍(斗之气三段) 斗破C编程入门系列之三:数据结构(斗之气三段) 斗破C编程入门系列之…...

目前美国的互联网环境
随着科技的迅猛发展,互联网已经成为了现代社会不可或缺的一部分。作为全球科技创新的领导者之一,美国在互联网领域拥有着丰富的资源和先进的技术。本文将对美国目前的互联网环境进行探讨,包括网络基础设施、网络安全、数字经济以及互联网对社…...

从最小作用量原理推导牛顿三大定律
从最小作用量原理推导牛顿三大定律 引言 在物理学中,牛顿三大定律是描述经典力学中物体运动的基本定律。然而,这些定律并不是孤立存在的,它们可以从一个更为普遍的原理——最小作用量原理中推导出来。最小作用量原理是一个深刻而优雅的理论…...

【系统集成项目管理工程师教程】第4章 信息系统架构
教程内容总结,供参考,有错误请指正,友好交流。 4.架构基础 4.1.1指导思想 4.1.2设计原则 原则内容:包括坚持以人为本、创新引领、问题导向、整体协同、安全可控、科学实施等,这些原则应基于组织的信念和价值观&…...
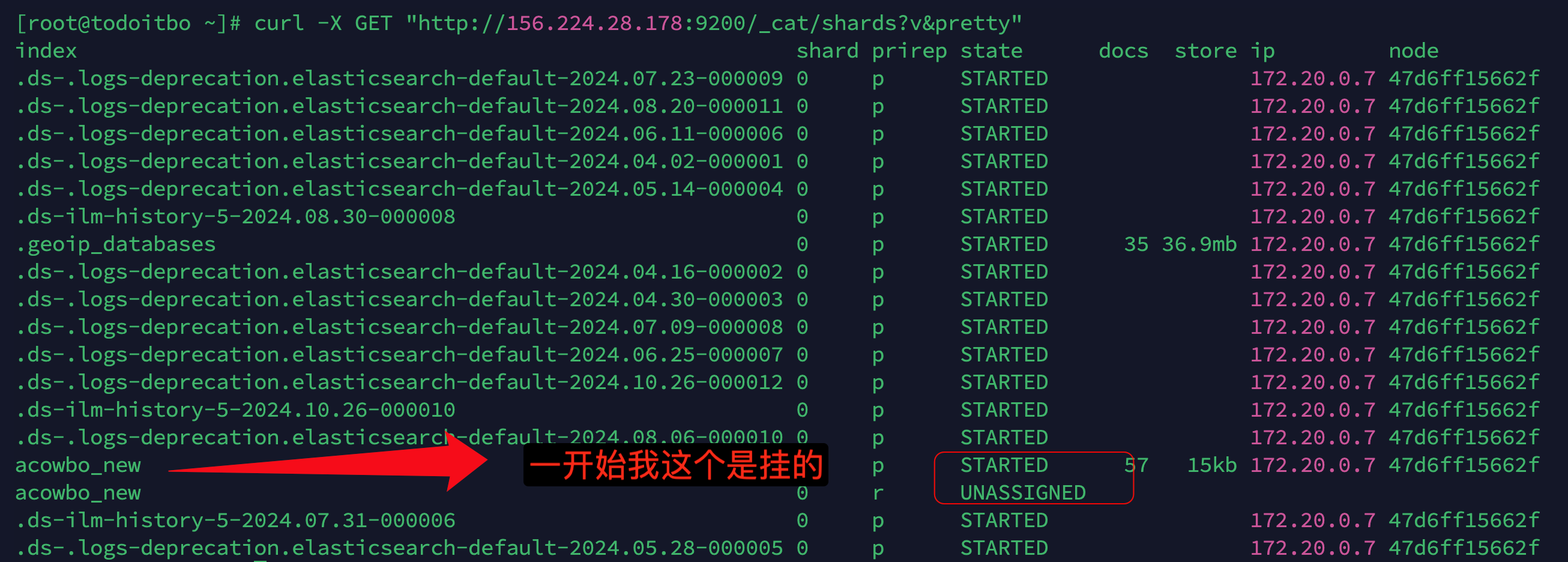
docker下迁移elasticsearch的问题与解决方案
欢迎来到我的博客,代码的世界里,每一行都是一个故事 🎏:你只管努力,剩下的交给时间 🏠 :小破站 docker下迁移elasticsearch的问题与解决方案 数据挂载报错解决权限问题节点故障 直接上图&#x…...

占地1.1万平,2亿投资的智能仓储系统:高架库、AGV、码垛机器人……
导语 大家好,我是社长,老K。专注分享智能制造和智能仓储物流等内容。 我国调味料市场近年来展现出惊人的增长潜力,各大品牌纷纷加大投入,力求在竞争中脱颖而出。 广东美味鲜调味食品有限公司,作为行业内的佼佼者&#…...

一个小程序如何对接多个收款账户?
背景 我又来了,之前对接过网约巴士系统 网约巴士旅游专线平台搭建历程,运营了两年多了。在运营中完善、在完善中学习,一直是不变的真理。有一句话说得好:先做一个垃圾、用起来再说。 今天又需要升级了,需求是&#…...

L2G4000 InternVL 部署微调实践闯关任务
一、理解多模态大模型的常见设计模式,可以大概讲出多模态大模型的工作原理。 视频地址 开源的多模态大模型:InternVL,Qwen-VL,LLaVA 闭源的:GPT-4o 研究重点:不同模态特征空间的对齐 BLIP2 将图像特征对…...

asynDriver-6-端口驱动
本地串口 drvAsynSerialPort驱动支持设备连接到IOC上串口。 用drvAsynSerialPortConfigure和asynSetOption命令配置串口: drvAsynSerialPortConfigure("portName","ttyName",priority,noAutoConnect,noProcessEosIn) asynSetOption("po…...

[免费]基于Python的Django+Vue3在线考试系统【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的基于Python的DjangoVue3在线考试系统,分享下哈。 项目视频演示 【免费】基于Python的DjangoVue3在线考试系统 Python毕业设计_哔哩哔哩_bilibili 项目介绍 本论文提出并实现了一种基于Python…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
