初识动态规划(由浅入深)
🤓 动态规划入门与进阶指南 📘
动态规划(Dynamic Programming, DP)是一种非常经典的📐算法方法,特别适合用来解决那些有大量重复计算的问题🌀。它可以将复杂的问题拆分为小问题🧩,然后一步一步地找到最终答案🎯。本文将介绍动态规划的基本概念💡,讲解它的好处👍,并通过一些例子展示动态规划的用法,还会与简单的暴力求解方法进行对比⚖️。最后,我们会讨论一些更复杂的例子,帮助你更好地理解动态规划。
❓ 什么是动态规划?
动态规划是一种把问题分成更小的子问题🔍,并用这些子问题的答案来解决整个问题的方法。动态规划最常用于具有 重叠子问题♻️ 和 最优子结构⭐ 的问题。
- 重叠子问题♻️:一个大问题可以被分成多个小问题🧩,而且这些小问题会被多次求解。
- 最优子结构⭐:问题的最优解可以通过其子问题的最优解来构造🛠️。
通过记住每个子问题的答案📝,动态规划可以避免重复计算,显著提高效率⏱️。
在应用动态规划时,我们通常会使用一个状态数组📊来表示每个小问题的解,然后使用状态转移方程来描述如何从这些子问题得到最终答案🏁。动态规划的核心思想是利用之前已经计算出的结果来避免重复工作。
📊 经典实例对比
1️⃣ 斐波那契数列
🔢 问题描述
斐波那契数列的定义是:
- F(0) = 0, F(1) = 1
- F(n) = F(n-1) + F(n-2),当 n >= 2
目标是计算斐波那契数列的第 n 项📍。
💥 暴力递归求解
// 递归暴力求解
// 时间复杂度:O(2^n)
public static int fibonacciRecursive(int n) {if (n <= 1) {return n;}return fibonacciRecursive(n - 1) + fibonacciRecursive(n - 2);
}
这种暴力方法简单直接🌀,但它的时间复杂度是 O(2^n),因为它会重复计算很多相同的子问题🔄。对于较大的 n 值,这种方法效率非常低⚠️。
🚀 动态规划求解
我们可以使用动态规划,通过记忆化或从底向上的方式来避免重复计算:
// 动态规划求解(自底向上)
// 时间复杂度:O(n),空间复杂度:O(n)
public static int fibonacciDP(int n) {if (n <= 1) {return n;}int[] dp = new int[n + 1];dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];
}
使用动态规划,我们可以将时间复杂度降低到 O(n),并且通过记忆中间结果来减少重复计算🗂️。虽然空间复杂度是 O(n),但这个方法能显著减少计算时间⏳。
🛠️ 优化后的动态规划解法
我们可以进一步优化空间复杂度,只存储最近的两个值:
// 优化后的动态规划求解
// 时间复杂度:O(n),空间复杂度:O(1)
public static int fibonacciOptimized(int n) {if (n <= 1) {return n;}int prev = 0, curr = 1;for (int i = 2; i <= n; i++) {int next = prev + curr;prev = curr;curr = next;}return curr;
}
在这个实现中,我们将空间复杂度降低到了 O(1)。这种方法的核心是每次只保留最近的两个斐波那契数,因此大大节省了内存💾。
2️⃣ 0/1 背包问题 🎒
❓ 问题描述
有 n 个物品,每个物品有一定的重量和价值⚖️💰,背包的最大容量是 W。目标是在不超过容量的情况下,使背包内的物品总价值最大化💵。
- 重量数组:weights = [2, 3, 4, 5]
- 价值数组:values = [3, 4, 5, 6]
- 背包容量:W = 5
💥 暴力求解
暴力求解就是穷举所有可能的组合🔢,找到最大价值💰。时间复杂度为 O(2^n),因为每个物品都有 “选择” 或 “不选择” 两种可能。这种方法在物品数量多时非常低效⚠️。
🚀 动态规划求解
我们可以用动态规划,通过创建一个二维数组📊来存储子问题的解。状态转移方程为:
dp[i][w]表示前 i 个物品在容量为 w 时的最大价值。- 转移方程为:
- 如果不选第 i 个物品:
dp[i][w] = dp[i-1][w] - 如果选第 i 个物品:
dp[i][w] = max(dp[i-1][w], dp[i-1][w - weights[i-1]] + values[i-1])
- 如果不选第 i 个物品:
// 动态规划求解 0/1 背包问题
// 时间复杂度:O(n * W),空间复杂度:O(n * W)
public static int knapsack(int[] weights, int[] values, int W) {int n = weights.length;int[][] dp = new int[n + 1][W + 1];for (int i = 1; i <= n; i++) {for (int w = 0; w <= W; w++) {if (weights[i - 1] <= w) {dp[i][w] = Math.max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + values[i - 1]);} else {dp[i][w] = dp[i - 1][w];}}}return dp[n][W];
}
时间和空间复杂度都是 O(n * W)。动态规划避免了重复计算,从而显著提高了求解效率⏳。
🛠️ 优化空间复杂度
我们可以将二维数组优化为一维数组,只需记录前一行的数据:
// 优化后的动态规划求解 0/1 背包问题
// 时间复杂度:O(n * W),空间复杂度:O(W)
public static int knapsackOptimized(int[] weights, int[] values, int W) {int n = weights.length;int[] dp = new int[W + 1];for (int i = 0; i < n; i++) {for (int w = W; w >= weights[i]; w--) {dp[w] = Math.max(dp[w], dp[w - weights[i]] + values[i]);}}return dp[W];
}
通过使用一维数组,空间复杂度可以降低到 O(W),这使得动态规划在处理大规模的背包问题时更有效🔋。
至于为什么要反向遍历呢?
3️⃣ 编辑距离问题 ✍️
❓ 问题描述
编辑距离是指把一个字符串转换为另一个字符串所需的最少操作次数🔄。允许的操作包括插入、删除和替换字符。比如,把 “kitten” 变成 “sitting” 需要 3 次操作。
🚀 动态规划求解
我们可以使用动态规划来解决这个问题。dp[i][j] 表示把 word1[0:i] 变成 word2[0:j] 需要的最小操作次数🔢。
状态转移方程为:
- 如果
word1[i-1] == word2[j-1],则dp[i][j] = dp[i-1][j-1] - 否则,
dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1] + 1)
// 编辑距离的动态规划解法
// 时间复杂度:O(m * n),空间复杂度:O(m * n)
public static int editDistance(String word1, String word2) {int m = word1.length();int n = word2.length();int[][] dp = new int[m + 1][n + 1];for (int i = 0; i <= m; i++) {for (int j = 0; j <= n; j++) {if (i == 0) {dp[i][j] = j;} else if (j == 0) {dp[i][j] = i;} else if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = 1 + Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1]));}}}return dp[m][n];
}
📚 更多经典动态规划案例
4️⃣ 最长公共子序列(LCS)🔗
最长公共子序列是在两个字符串中同时出现的最长子序列。我们可以用动态规划解决,通过定义 dp[i][j] 表示 text1[0:i] 和 text2[0:j] 的最长公共子序列的长度。
5️⃣ 最长上升子序列(LIS)📈
最长上升子序列的目标是在一个数组中找到最长的子序列,使得子序列中的每个元素都比前一个元素大⬆️。动态规划通过维护一个状态数组来解决。
6️⃣ 矩阵链乘法问题 🔗✖️
矩阵链乘法问题是为了找到一种最优方式来计算一系列矩阵的乘法次数,使得计算量最少。动态规划可以帮助找到这种最优计算方式。
7️⃣ 最小路径和 🛤️
在一个 m x n 的网格中找到从左上角到右下角的最小路径和🚶。动态规划可以通过定义 dp[i][j] 表示到达位置 (i, j) 的最小路径和来解决。
🤔 动态规划的好处总结
-
避免重复计算♻️:动态规划通过存储子问题的解来避免重复计算,从而大大降低时间复杂度⏱️。例如,斐波那契数列的暴力求解是 O(2^n),而动态规划可以做到 O(n)。
-
自底向上的求解方式⬇️⬆️:动态规划通过从小问题到大问题的解决方法,避免了递归的栈开销,减少了栈溢出的风险⚠️。
-
适用于重叠子问题和最优子结构的问题💡:很多问题,比如背包问题、编辑距离、最长公共子序列等,都可以用动态规划来高效解决。
-
时间与空间的平衡⚖️:动态规划通常需要更多的内存,但通过优化可以降低空间复杂度,例如滚动数组📉。
-
适用范围广🌍:动态规划可以用来解决很多不同类型的问题,从简单的数列到复杂的字符串和路径优化问题。
🔚 结论
动态规划是一种非常强大和有效的算法思想,通过记忆中间结果和从小到大的求解方法,它能够大幅度提高解决问题的效率⏳。希望本文能帮助你理解动态规划的基本概念和如何应用💡。接下来你可以试着练习一些经典的动态规划问题,比如最长上升子序列、完全背包、矩阵链乘、编辑距离、最长公共子序列等。这些问题会帮助你更好地掌握动态规划的思想📚。此外,理解动态规划的优化技巧,比如滚动数组和空间压缩,也会对你解决算法问题大有帮助🛠️💪。
相关文章:

初识动态规划(由浅入深)
🤓 动态规划入门与进阶指南 📘 动态规划(Dynamic Programming, DP)是一种非常经典的📐算法方法,特别适合用来解决那些有大量重复计算的问题🌀。它可以将复杂的问题拆分为小问题🧩&a…...

关于大模型微调与训练的问题,大模型训练的难点在哪里?
前言 “ 大模型训练的难点不在于大模型本身,而在于训练数据 ” 这两天有一个小兄弟问我关于大模型训练的问题,然后他想自己训练一个小模型,但又不知道该怎么操作;所以,今天就再来讨论一下大模型的训练问题࿰…...

如何对数据库的表字段加密解密处理?
对于表格数据的加密处理,通常涉及到对数据库中存储的数据进行加密,以保护敏感信息。 Java示例(使用AES算法加密数据库表数据) 首先,你需要一个数据库连接,这里假设你使用的是JDBC连接MySQL数据库。以下是…...
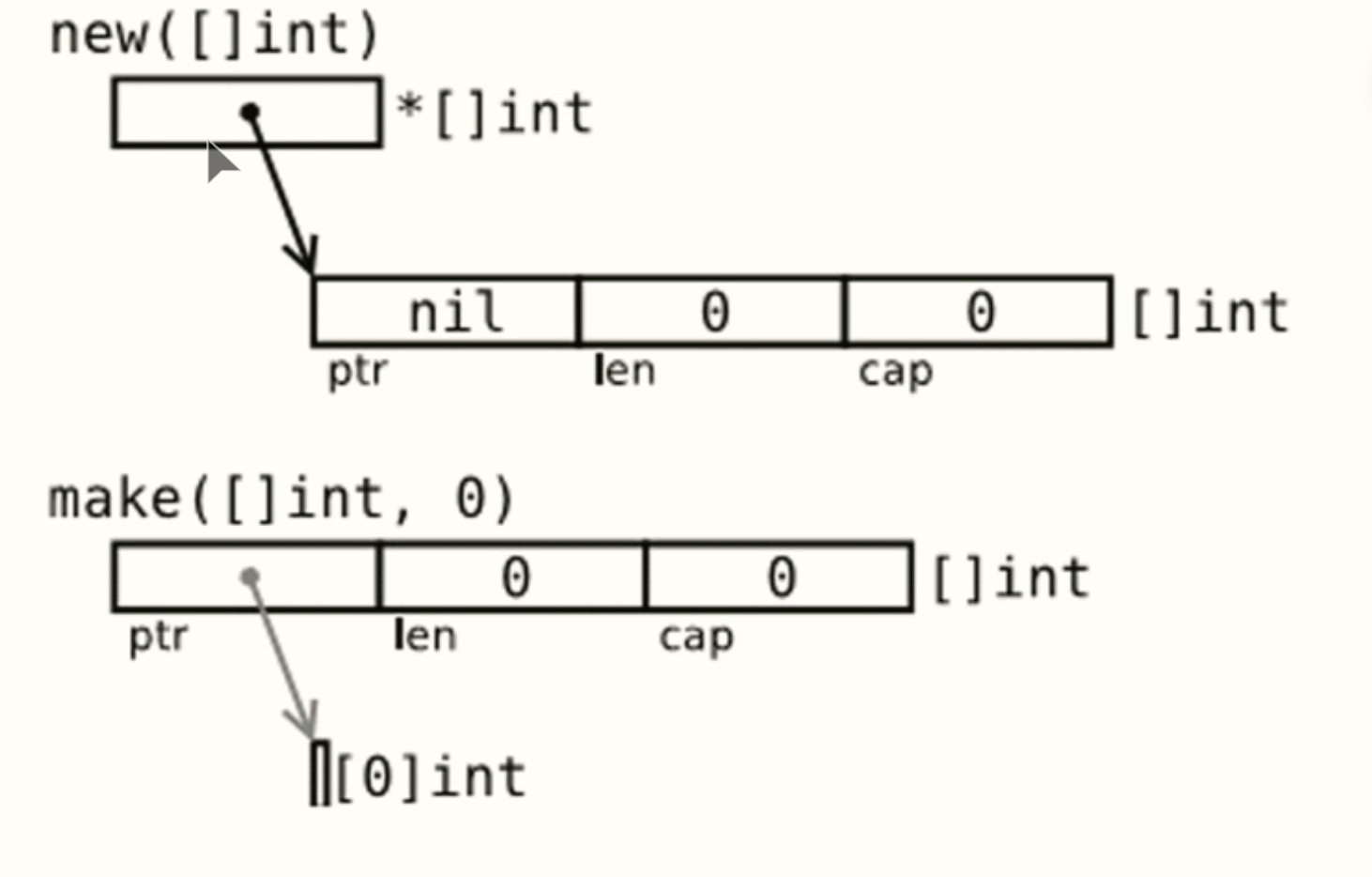
六、Go语言快速入门之数组和切片
文章目录 数组和切片数组:one: 数组初始化:two: 数组的遍历:three: 多维数组:four: 将数组传递给函数 切片(Slice):one: 切片的初始化:star: new和make区别 :two: 切片的使用:three: 将切片传递给函数:four: 多维切片:four: Bytes包:four: 切片和垃圾回收 📅 2024年…...

Java:数组的定义和使用(万字解析)
目录 1. 数组的概念 2. 数组的基础知识 2.1 数组的创建 \1. 基础创建格式: \2. 类似C语言的创建格式: 【错误的创建(初始化)格式】 2.2 数组的数据类型 2.3 数组的初始化 —— 两种方式 \1.动态初始化:(完全默认初始化) \2. 静态初…...

密码学简要介绍
密码学是研究编制密码和破译密码的技术科学,它研究密码变化的客观规律,主要包括编码学和破译学两大部分。 一、定义与起源 定义:密码学是研究如何隐密地传递信息的学科,在现代特别指对信息以及其传输的数学性研究,常被…...

2024.11月最新智能问答AI创作系统源码,GPT4.0多模态模型+AI换脸+AI智能体GPTs应用+AI绘画(Midjourney)+详细搭建部署教程
一、前言 SparkAi创作系统是一款基于ChatGPT和Midjourney开发的智能问答和绘画系统,提供一站式 AI B/C 端解决方案,AI大模型提问、AI绘画、专业版AI视频生成、文档分析、多模态识图理解、TTS & 语音识别对话、AI换脸、支持AI智能体应用(…...

江协科技STM32学习- P34 I2C通信外设
🚀write in front🚀 🔎大家好,我是黄桃罐头,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝…...

Python 继承、多态、封装、抽象
面向对象编程(OOP)是 Python 中的一种重要编程范式,它通过类和对象来组织代码。OOP 的四个核心概念是继承(Inheritance)、多态(Polymorphism)、封装(Encapsulation)和数据…...

在.net下后台设置前台UEditor编辑器不可编辑
今天手下有个问:当用户填写提交后,再次显示提交页面时,该页面的UEditor编辑器需要设置成不可编辑,怎么实现? 可以用后台调用前台js的方式实现: 例如: 前台页面: <div style&qu…...

Flutter CustomScrollView 效果-顶栏透明与标签栏吸顶
CustomScrollView 效果 1. 关键组件 CustomScrollView, SliverOverlapAbsorber, SliverPersistentHeader 2. 关键内容 TLDR SliverOverlapAbsorber 包住 pinned为 true 的组件 可以被CustomScrollView 忽略高度。 以下的全部内容的都为了阐述上面这句话。初阶 Flutter 开发知…...

【新手入门软件测试--该如何分辨前后端问题及如何定位日志--前后端问题分辨与日志定位查询问题】
前后端问题分辨与日志定位查询 一、前端问题1. 页面无法加载2. 样式错乱3. API请求失败4. 数据格式错误5. 跨域请求问题 二、后端问题6. 表单验证失败7. 数据库连接失败8. 请求超时9. 权限问题10. JavaScript运行错误 三、日志查询的方法1. 查看日志文件2. 过滤关键字3. 实时查…...

【Java Web】DAO模式及单例模式(含代码示例)
文章目录 JDBC封装DAO模式实体类DAO接口DAO实现类数据源配置基础DAO类业务逻辑层 单例模式饿汉式懒汉式 JDBC封装 JDBC(Java Database Connectivity)封装是一种将 JDBC 的基本操作和常见的数据库访问逻辑封装成易于使用的工具类或框架的方法。这样做的目…...

深入探讨SEO分析技巧助力网站流量提升
内容概要 在当前的数字化时代,SEO分析的重要性不言而喻。它是提升网站流量的关键工具,帮助站长有效地优化网站内容和结构。通过系统的SEO分析,站长可以掌握用户搜索行为和需求,从而制定出更具针对性的内容策略。例如,…...
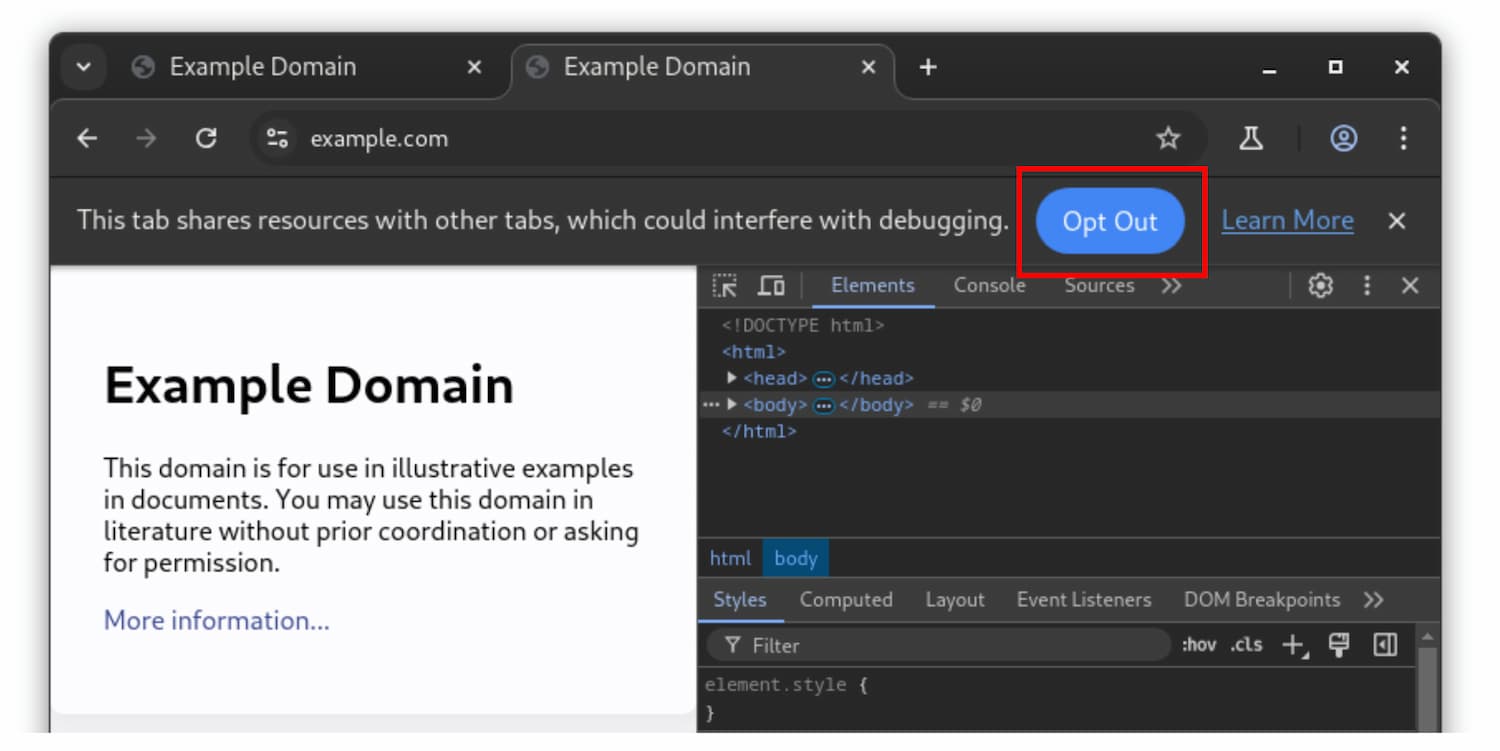
Chrome 130 版本开发者工具(DevTools)更新内容
Chrome 130 版本开发者工具(DevTools)更新内容 一、网络(Network)面板更新 1. 重新定义网络过滤器 网络面板获新增了一些过滤条件,这些过滤条件是根据反馈重新设计的,特定于类型的过滤条件保持不变&…...

深度学习基础知识-残差网络ResNet
目录 一、ResNet 的核心思想:残差学习(Residual Learning) 二、ResNet 的基本原理 三、ResNet 网络结构 1. 残差块(Residual Block) ResNet 的跳跃连接类型 2. 网络结构图示 四、ResNet 的特点和优势 五、ResNe…...
)
Linux云计算个人学习总结(二)
高级文件系统 一、RSYNC概述 1、作用:快速的文件复制工具(支持本地和远程),以及删除、查看等基本功能。 2、特点:支持实时(inotify、sersync)的增量备份工具3、模式:检查模式&#…...
--网络编程)
Java入门(7)--网络编程
Java网络编程:构建网络应用的基石 🌐 🎯 掌握Java网络编程,打造强大的网络应用! 在上一篇文章中,我们探讨了Java的I/O操作和反射机制。今天,让我们深入学习Java网络编程,了解如何构建…...

[思考记录]思维局限,以为懂了
最近配合整理一些内容,找到较早期的某些产品设计资料在翻阅回顾。在这次回顾过程中,发现当时自己的理解存在很多局限。 以资源体系的设计为例,那时自认为已经“懂了”,对相关的概念、作用关系、组成及实现等都有一定的了解&#x…...

力扣题目解析--最长公共前缀
题目 编写一个函数来查找字符串数组中的最长公共前缀。 如果不存在公共前缀,返回空字符串 ""。 示例 1: 输入:strs ["flower","flow","flight"] 输出:"fl"示例 2ÿ…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...


