2024年北京海淀区中小学生信息学竞赛校级预选赛试题

2024年北京海淀区中小学生信息学竞赛校级预选赛试题

题目总数：24    总分数：100

编程基础知识单选题

第 1 题    单选题

关于 2024年海淀区信息学竞赛的描述错误的是(   )

A.报名在网上报名系统进行

B.必须经过学籍所在学校的指导教师审核

C.学校预选赛达到一定分数可以晋级区级初赛

D.北京市对编程有兴趣的小学生都可以报名预选赛

第 2 题    单选题

下列是合法的C++变量名称的是(   )

A2a

B.2#4

C.a36

D.?a

E.180

第 3 题    单选题

关于C++赋值语句的写法一定错误的是(   )

A.

int a = 12;

B.

int a[]= {0};

C.

a[]= {3,6};

D.

strings="7;

E.

ch='1';

第 4 题    单选题

二进制数(1011001),对应的十进制数是(   )

A.

39

B.

49

C.

81

D.

89

E.

177

第 5 题    单选题

表达式 23 & 18 的运算结果为( )。

A.

2

B.

16

C.

18

D.

20

E.

23

第 6 题    单选题

将7人分成三组，要求任意两个组的人数差值不能超过1，则有( )种不同的分法。

A.

210

B.

105

C.

84

D.

420

E.

168

第 7 题    单选题

给定 10 个正整数，要求从小到大排序，最坏的情况下，需要( )次比较次数。

A.

50

B.

45

C.

40

D.

39

E.

36

第 8 题    单选题

下列相关描述中字符型变量ch能够得到字符a的选项是( )

A.

if strings ="abcad", ch = s[4]

B.

ch = 'A'+32

C.

ch = 65

D.

ch= 97

E.

ch ='A'-32

第 9 题    单选题

下列关于 C++中函数的说法中错误的是(  )

A.

每程序有且只有一个主函数

B.

函数都可以自己调用自己

C.

主函数是程序执行的入口

D.

递归函数是函数自己调用自己的典型代表

E.

函数不支持嵌套

第 10 题    单选题

关于运算符和表达式的说法错误的是(   )

A.

关系表达式运算结果是一个逻辑值

B.

赋值表达式只有一个运算结果

C.

逻辑表达式的运算结果仍然是一个逻辑值

D.

字符型变量不能参加算术运算 的相关知识

E.

算术运算符和赋值运算符可以构成复合运算符

第 11 题    单选题

下列关于循环语句不正确的是()

A.

for 语句能够实现确定次数的循环功能

B.

break 语句能够用来跳出循环语句

C.

while 语句能够实现不确定次数的循环功能

D.

continue 只是跳过本次循环

E.

while 语句专用来实现不确定次数的循环功能

第 12 题    单选题

定义数组 int a[3][2]={2,3,4,5,6,7},则下列数组元素的值为5的是()

A.

a[1][0]

B.

a[1][1]

C.

a[2][0]

D.

a[2][1]

E.

a[2][2]

程序问题单选题

第 13 题    单选题

阅读下面的C++程序，输入一个整数 36，则输出的结果为()

#include<bits/stdc++.h>
using namespace std;
int n,cnt;
int main()
{cin>>n;for(int i=l;i<n;i++)if(n%i==0) cnt++;cout<ccnt;return 0;
}

A.

3

B.

4

C.

6

D.

8

E.

12

第 14 题    单选题

阅读下面的程序，输入两个整数 54 和 120，则输出的结果为( )

#include<bits/stdc++.h>

using namespace std;

int n,cnt,m;

int main()

{

    cin>>n>>m;

    for(int i=1;i<=n;i++)

    {

        if(m%i==0 && n‰i==0) cnt++;

        if(cnt==6) break;

    }

    cout<<cnt;

    return 0;

}

A.

2

B.

3

C.

4

D.

5

E.

6

第 15 题    单选题

阅读下面的c++程序，输入两个整数 24和 36，则输出的结果为()

#include<bits/stdc++.h>
using namespace std;
int a,b,c,d;
int main(){cin>>a>>b;c=min(a,b);for(int i=c;i>0;i--)if(a%i==0 && b%i==0){d=i;break;}cout<<a*b/d;return 0;
}

A.

12

B.

24

C.

36

D.

72

E.

180

第 16 题    单选题

阅读下面的C++程序，输入一个整数 40，则输出的结果为 (   )

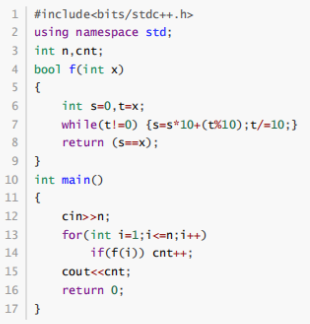
#include<bits/stdc++.h>
using namespace std;
int n,cnt;
bool f(int x)
{int s=0,t=x;while(t!=0){s=s*10+(t%10);t/=10;}return(s==x);
}
int main()
{cin>>n;for(int i=l;i<=n;i++)if(f(i)) cnt++;cout<<cnt;return 0;
}

A.

10

B.

11

C.

12

D.

13

E.

14

第 17 题    单选题

阅读下面的C++程序，输入一个整数 30，则输出的结果为(   )

#include<bits/stdc++.h>
using namespace std;
int n,a[10010];
int main()
{cin>>n;a[1]=1;for(int i=2;i<=10000;i++){if(a[i]==0) continue;for(int j=2;j<=10000/i;j++)a[i*j]=1;}for(int i=1;i<=n;i++) a[i]=a[i-1]+(1-ai);cout<<aln];return 0;
}

A.

6

B.

10

C.

12

D.

18

E.

30

第 18 题    单选题

阅读下面的C++程序，分别输入两个整数 73和 77，则输出的结果分别为(   )

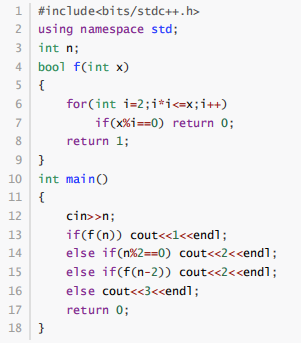
#include<bits/stdc++.h>
using namespace std;
int n;
bool f(int x)
{for(int i=2;i*i<x;i++)if(x%i==0) return 0;return 1;
}
int main()
{cin>>n;if(f(n))cout<<l<<end1;else if(n%2==0)cout<<2<<end1;else if(f(n-2))cout<<2<<end1;else cout<<3<<endl;return 0;
}

A.

1 2

B.

1 3

C.

2 3

D.

3 2

E.

3 1

第 19 题    单选题

阅读下面的C++程序，输入两个整数 108 和 120，则输出的结果为(   )

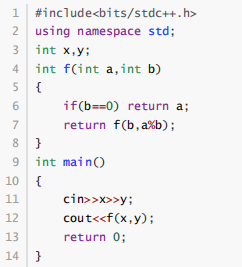
#include<bits/stdc++.h>
using namespace std;
int x,y;
int f(int a,int b)
{if(b==0) return a;return f(b,a%b);
}
int main()
{cin>>x>>y;cout<<f(x,y);return 0;
}

A.

12

B.

9

C.

6

D.

3

E.

2

第 20 题    单选题

阅读下面的C++程序，输出的结果为(   )

#include<bits/stdc++.h>
using namespace std;
int i,n,ans;
int main()
{i=1;while(1){i++;if(i%7!=0) continue;int cnt=0;for(int j=2;j<i;j++)if(i%j==0)cnt++;if(cnt==6){ans=i;break;}}cout<<ans;return 0;
}

A.

28

B.

42

C.

56

D.

168

E.

280

阅读问题单选题

第 21 题    单选题

手机操作系统:

一款新的智能手机的菜单上有”个应用程序，编号从1到 n，每个应用程序都有自己的图标。这些图标位于不同的屏幕上，每个屏幕上有人个图标，第1到第k号图标位于第一个屏幕上，第k+1到第2k号图标位于第二个屏幕上，以此类推，最后一个屏幕可能部分为空。初始时，手机菜单显示的是第 1号屏幕，要启动位于第 t号屏幕上的应用程序，需要执行以下操作:首先滚动到所需的屏幕号，需要做t-1 次操作，然后再用一次操作，双击所需应用程序的图标以启动它。应用程序启动后，菜单自动返回到第一个屏幕，做好启动下一个应用程序的准备，即需要再次从 1号屏幕开始操作。

给定应用程序图标在菜单中的初始顺序，但在使用过程中，它们的顺序会发生变化。变化规则:应用程序启动后，系统会将该应用程序的图标位置与前一个应用程序的图标位置交换，前一个应用程序的图标可能位于相邻的屏幕上，当启动的应用程序的图标已经处于第一个位置时，图标的位置不会改变。一个应用程序可以被多次启动。注意区分应用程序的编号以及位置，这是两个不同的变量，

现在按照上述规则，给定以下数据:第一行包含三个整数n=5，m=4，k=2分别表示应用程序的总个数、计划要启动的应用程序的个数和每个屏幕上满屏时可以包含的应用程序的个数，第二行包含5个整数 3，1，5，2，4，恰好为1到5一个排列，依次为1到5号应用程序的图标初始位置的编号，第三行包含 4个整数 4，4，4，4，依次为计划启动的 4个应用程序的编号。

针对给定的这些数据，需要( )次操作才能完成全部应用程序的启动。

A.

9

B.

8

C.

7

D.

6

E.

5

第 22 题    单选题

视频压缩问题:

网络中心有k个服务器用于压缩上传到网站上的视频，服务器压缩视频时按照视频上传时间的先后顺序依次进行。每个服务器1秒可以压缩1分钟时长的视频，同一时间段每个服务器只能压缩一个视频，多个服务器可以一起工作，同一个视频只能在同一个服务器上压缩。当所有服务器都在工作时，视频按照上传时间的先后顺序排队等待，有服务器空闲就立即开始工作。现在给定服务器的数量k=4，上传到网站上的视频数目 n = 10，已知这 10 个视频分别是第 1,2,3,...,10 秒钟上传的(假设视频上传是瞬间完成的)，除了第2个和第8个视频长度是2分钟，其它视频的长度都是1分钟。关于每个视频完成压缩的时间，下列说法错误的是()

A.

第 9 个视频是在第 11 秒完成压缩的

B.

第 8 个视频是在第 10 秒完成压缩的

C.

第 6 个视频是在第 7 秒完成压缩的

D.

第 3 个视频是在第 4 秒完成压缩的

E.

第 2 个视频是在第 4 秒完成压缩的

第 23 题    单选题

掷骰子游戏:

淘淘没事喜欢和小朋友们一起完掷骰子游戏，过去的骰子多是小的正方体，有六个面，分别标有1到6的六个圆点，分别代表数字1到6，今天淘淘带来了一套新玩法:他有 4个骰子，这 4个骰子编号分别为 1,2,3,4，它们分别有 5,6,7,8个面，一个骰子有工个面，则这 工个面上分别标示1到ェ的数字，同一个骰子每个面上的数字互不相同。淘淘把这 4个骰子同时投掷出去，计算得知 4个骰子显示的数字之和为 22。则下列说法正确的是( )

A.

所有骰子上每个面上的数字都有可能出现

B.

第 1个骰子上的所有的数字都可能出现,

C.

第 2个骰子上的所有的数字都可能出现!

D.

第 3 个骰子上的所有的数字都可能出现

E.

第 4个骰子上的所有的数字都可能出现!

第 24 题    单选题

小猴爬山问题:

一只小猴爬山，一共进行了8天，淘淘负责记录小猴每天爬山结束时的海拔高度，但由于字迹潦草，有些记录连他自己都认不出来了，现在能确定的只有第 2天所在海拔高度是0，第8天所在海拔高度也是0，已知小猴任意连续两天所在的海拔高度之差不会超过1，则这8天的海拔高度记录中其可能到过的最高海拔高度是(   )

A.

1

B.

2

C.

3

D.

4

E.

来源：6547网 www.6547.cn/doc/dfqr416h7i