多面体定义+多面体是凸集+多面体的重要性质
文章目录
- 多面体定义
- 多面体是凸集
- 多面体重要性质
- 1. 有界多面体(Convex Polytope)
- 2. 无界多面体(Unbounded Polyhedron)
- 3. 极点表示(顶点形式)与极点-极射线表示定理
在数学中, 多面体(polyhedron)是指由有限个线性不等式和等式定义的一个凸集合。具体地说, 多面体是线性约束条件下的解空间,也可以看作是凸多面体的推广。在优化、线性规划和几何中,多面体的定义尤为重要。
多面体定义
在 n n n-维空间 R n \mathbb{R}^n Rn中,一个多面体可以定义为满足有限个线性不等式和等式的所有点的集合。
标准定义:
一个集合 P ⊆ R n P \subseteq \mathbb{R}^n P⊆Rn是多面体,当且仅当存在一个矩阵 A ∈ R m × n A \in \mathbb{R}^{m \times n} A∈Rm×n和一个向量 b ∈ R m b \in \mathbb{R}^m b∈Rm,使得 P P P可以表示为
P = { x ∈ R n : A x ≤ b } 。 P = \{ x \in \mathbb{R}^n : A x \leq b \}。 P={x∈Rn:Ax≤b}。
这里:
- A x ≤ b A x \leq b Ax≤b表示一组线性不等式。
- x ∈ R n x \in \mathbb{R}^n x∈Rn表示我们考虑的点在 n n n-维空间中。
更一般地,多面体还可以包括一些线性等式,即:
P = { x ∈ R n : A x ≤ b , C x = d } 。 P = \{ x \in \mathbb{R}^n : A x \leq b, \ C x = d \}。 P={x∈Rn:Ax≤b, Cx=d}。
其中:
- C ∈ R k × n C \in \mathbb{R}^{k \times n} C∈Rk×n和 d ∈ R k d \in \mathbb{R}^k d∈Rk定义了线性等式的约束。
在这个定义中,多面体的边界由这些不等式和等式所定义的半空间的交集来确定。
所以多面体的定义为:
一个集合 P ⊆ R n P \subseteq \mathbb{R}^n P⊆Rn是多面体,当且仅当存在一个矩阵 A ∈ R m × n A \in \mathbb{R}^{m \times n} A∈Rm×n和一个向量 b ∈ R m b \in \mathbb{R}^m b∈Rm, C ∈ R k × n C \in \mathbb{R}^{k \times n} C∈Rk×n和 d ∈ R k d \in \mathbb{R}^k d∈Rk,使得:
P = { x ∈ R n : A x ≤ b , C x = d } , P = \{ x \in \mathbb{R}^n : A x \leq b, \ C x = d \}, P={x∈Rn:Ax≤b, Cx=d},
其中:
- A x ≤ b A x \leq b Ax≤b是一组定义边界的线性不等式【半空间】。
- C x = d C x = d Cx=d是一组定义面的线性等式(可选)【超平面】。
多面体是凸集
从几何上看,多面体可以被认为是一个凸的几何对象。其几何结构可以分解为顶点、边、面等,取决于空间的维数。例如:
- 在三维空间中,一个多面体可能是立方体、四面体等,由平面限定的几何体。
- 在二维空间中,满足线性不等式的集合即为多边形。
多面体之所以凸,是因为线性不等式和等式的交集形成了一个凸集。这意味着,对于任何位于多面体内的两点 x , y ∈ P x, y \in P x,y∈P,连接这两点的线段也完全位于 P P P内,即
∀ λ ∈ [ 0 , 1 ] , λ x + ( 1 − λ ) y ∈ P 。 \forall \lambda \in [0, 1], \ \lambda x + (1 - \lambda) y \in P。 ∀λ∈[0,1], λx+(1−λ)y∈P。
多面体重要性质
-
有界多面体:当多面体的定义约束使得 P P P的边界是有限的时,我们称其为有界多面体,通常也叫做凸多面体(convex polytope)。
-
无界多面体:当多面体的定义约束不完全封闭 P P P时,该多面体可能是无界的。
-
极点表示(顶点形式):多面体也可以通过顶点的凸组合来表示。这是极点-极射线表示定理的内容。
1. 有界多面体(Convex Polytope)
一个有界多面体,或称为凸多面体,是一个由有限个线性不等式所定义的有限闭凸集合,即它的边界是有限的。这类多面体的几何形状是封闭的,并且在有限的空间中存在。
数学定义:
在 R n \mathbb{R}^n Rn 中,一个集合 P P P 称为有界多面体或凸多面体,当且仅当存在有限个向量 v 1 , v 2 , … , v k ∈ R n v_1, v_2, \dots, v_k \in \mathbb{R}^n v1,v2,…,vk∈Rn 和权重 λ i ≥ 0 \lambda_i \geq 0 λi≥0,满足:
P = { x ∈ R n : x = ∑ i = 1 k λ i v i , ∑ i = 1 k λ i = 1 } 。 P = \left\{ x \in \mathbb{R}^n : x = \sum_{i=1}^k \lambda_i v_i, \quad \sum_{i=1}^k \lambda_i = 1 \right\}。 P={x∈Rn:x=i=1∑kλivi,i=1∑kλi=1}。
也就是说, P P P 是由其顶点的凸组合(convex combination)所生成的集合。
-
凸组合:凸组合表示权重的非负性和总和为1,从而保证了组合后的点仍然在多面体内部。
-
这种定义也表明,有界多面体是凸的,即如果 x , y ∈ P x, y \in P x,y∈P,那么对任意 λ ∈ [ 0 , 1 ] \lambda \in [0,1] λ∈[0,1], λ x + ( 1 − λ ) y ∈ P \lambda x + (1 - \lambda) y \in P λx+(1−λ)y∈P。
-
有限个向量的非负线性组合(系数非负且求和为1)+有界多面体必定是凸的+ 有界多面体是顶点的凸组合构成的
2. 无界多面体(Unbounded Polyhedron)
一个无界多面体是由线性不等式或等式约束定义的集合,但这些约束并不完全限制集合在空间中的边界,使得多面体在某些方向上可以延伸到无限远。
数学定义:
在 R n \mathbb{R}^n Rn 中,一个集合 P P P 称为无界多面体,当且仅当它可以表示为:
P = { x ∈ R n : A x ≤ b } , P = \left\{ x \in \mathbb{R}^n : A x \leq b \right\}, P={x∈Rn:Ax≤b},
其中 A ∈ R m × n A \in \mathbb{R}^{m \times n} A∈Rm×n 是一个矩阵, b ∈ R m b \in \mathbb{R}^m b∈Rm 是向量,且存在非零向量 d ∈ R n d \in \mathbb{R}^n d∈Rn,使得
x + λ d ∈ P , ∀ λ ≥ 0 。 x + \lambda d \in P, \quad \forall \lambda \geq 0。 x+λd∈P,∀λ≥0。
这表明,可以沿着某个方向 d d d 无限地延伸 x x x,而仍然保持在 P P P 内,因此 P P P 是无界的。
- 无界性:多面体的无界性来自于满足约束 A x ≤ b A x\leq b Ax≤b 的同时,存在一条无限延伸的方向。
- 满足线性不等式的时候,存在一条无限延伸的方向可以延伸到无限远
3. 极点表示(顶点形式)与极点-极射线表示定理
极点表示定理(或称顶点形式)指出,每个多面体都可以表示为其极点(顶点)的凸组合,且对于无界多面体,还需要包含其极射线的正组合。
- 极点:极点是多面体的顶点,表示那些不能通过其他点的凸组合来表示的点。
- 极射线:对于无界多面体,极射线(或称为方向向量)是那些可以沿其方向无限延伸的方向。
数学定义:
设 P ⊆ R n P \subseteq \mathbb{R}^n P⊆Rn 是一个多面体。根据极点-极射线表示定理, P P P 可以表示为其极点和极射线的凸组合:
P = { x ∈ R n : x = ∑ i = 1 k λ i v i + ∑ j = 1 l μ j d j , λ i ≥ 0 , ∑ i = 1 k λ i = 1 , μ j ≥ 0 } 。 P = \left\{ x \in \mathbb{R}^n : x = \sum_{i=1}^k \lambda_i v_i + \sum_{j=1}^l \mu_j d_j, \quad \lambda_i \geq 0, \ \sum_{i=1}^k \lambda_i = 1, \ \mu_j \geq 0 \right\}。 P={x∈Rn:x=i=1∑kλivi+j=1∑lμjdj,λi≥0, i=1∑kλi=1, μj≥0}。
其中:
- v 1 , v 2 , … , v k v_1, v_2, \dots, v_k v1,v2,…,vk 是 P P P 的极点;
- d 1 , d 2 , … , d l d_1, d_2, \dots, d_l d1,d2,…,dl 是 P P P 的极射线;
- λ i \lambda_i λi 和 μ j \mu_j μj 分别为非负权重,使得点 x x x 是这些顶点和射线的线性组合。
解释:
- 有界多面体仅由其极点的凸组合生成,因此没有极射线项;
- 无界多面体需要极点和极射线的组合,才能表示出所有在多面体内部的点。
- 有界多面体=极点的凸组合(没有极线);无界多面体==极点+极线(多面体内部)
相关文章:

多面体定义+多面体是凸集+多面体的重要性质
文章目录 多面体定义多面体是凸集多面体重要性质1. 有界多面体(Convex Polytope)2. 无界多面体(Unbounded Polyhedron)3. 极点表示(顶点形式)与极点-极射线表示定理 在数学中, 多面体ÿ…...

为什么 Allow 配合 meta noindex 比使用Disallow好?
为什么 Allow 配合 meta noindex 1、Disallow 的问题 当你使用 Disallow: / 时: 爬虫根本不会访问你的页面 因此永远看不到你的 meta noindex 标签 如果有其他网站链接到你的页面,Google 可能还是会将其编入索引(因为它无法确认你是否真的…...

通讯学徒学习日记
本章内容为 长期更新模式,目前入职的第三天,学徒状态。 文章目录 前言开始接水晶头、接光纤水晶头接光纤 PON(GPON 、EPON)AON 和 PON 的详解AONPON 前言 编程虽然是爱好,但确实也想把这份爱好变成工作。但是对于目前刚…...

迪杰斯特拉算法
迪杰斯特拉算法 LeetCode 743. 网络延迟时间 https://blog.csdn.net/xiaoxi_hahaha/article/details/110257368 import sysdef dijkstra(graph, source):"""dijkstra算法:param graph: 邻接矩阵:param source: 出发点,源点:return:""&…...

IPsec传输模式与隧道模式的深度解析及应用实例
随着网络安全威胁的日益严峻,IPsec作为网络层安全协议,其传输模式与隧道模式的选择对确保通信安全至关重要。本文旨在深入探讨这两种模式的差异,并通过实际案例展示其应用。 一、传输模式和隧道模式的详细描述 传输模式: 应用场景…...

实现Vue3/Nuxt3 预览excel文件
安装必要的库 npm install xlsx 创建一个组件来处理文件上传和解析: 在src/components 目录下创建一个名为 ExcelPreview.vue 的文件 <template> <div> <input type"file" change"handleFileUpload" /> <table v-if"…...

【AI落地应用实战】HivisionIDPhotos AI证件照制作实践指南
最近在网上发现了一款轻量级的AI证件照制作的项目,名为HivisionIDPhotos。它利用AI模型实现对多种拍照场景的识别、抠图与证件照生成,支持轻量级抠图、多种标准证件照和排版照生成、纯离线或端云推理、美颜等功能。此外,项目还提供了Gradio D…...

php实现sl651水文规约解析
SL651-2014-《水文监测数据通信规约》 1、要素解析说明 39 23 00 00 03 45 0x39查标识符得知为:39H Z 瞬时河道水位、潮位,我们定义为水位 0x23 按照要素标识符的规定,高5bit,低3bit,00100 011 对应的转换为10进制为4与3,也就是水位数据占用4字节,小…...
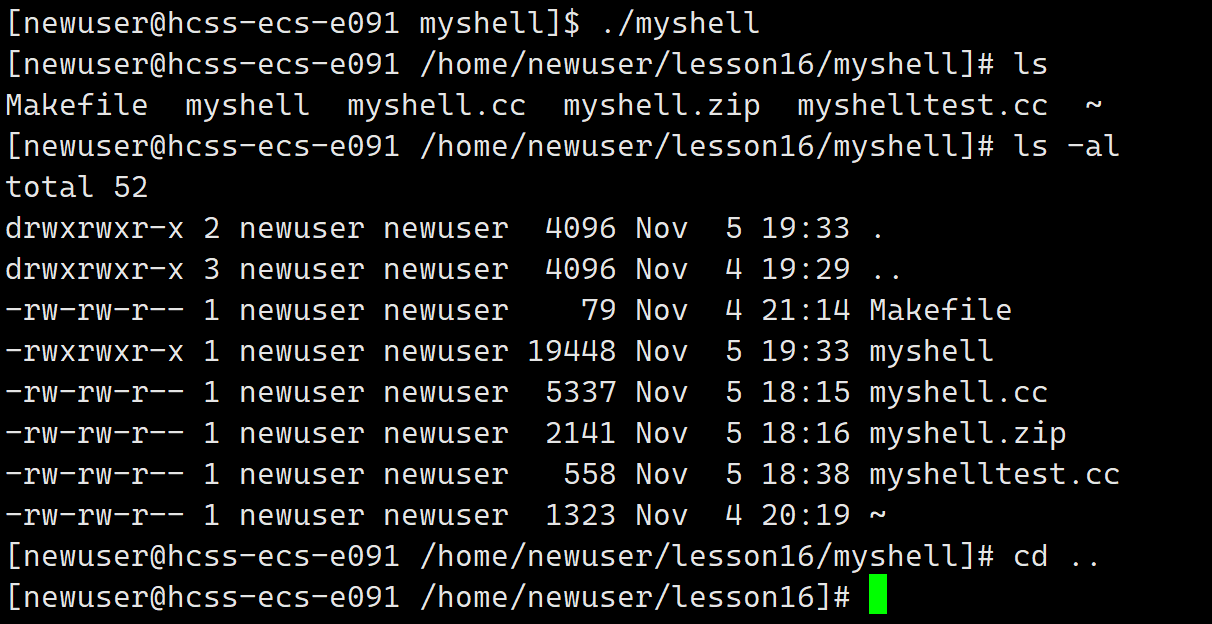
【Linux】简易版shell
文章目录 shell的基本框架PrintCommandLineGetCommandLineParseCommandLineExecuteCommandInitEnvCheckAndExecBuildCommand代码总览运行效果总结 shell的基本框架 要写一个命令行我们首先要写出基本框架。 打印命令行获取用户输入的命令分析命令执行命令 基本框架的代码&am…...

宝塔Linux面板安装PHP扩展失败报wget: unable to resolve host address ‘download.bt.cn’
一、问题: 当使用宝塔面板安装PHP扩展失败出现如下错误时 Resolving download.bt.cn(download.bt.cn)...failed: Connection timed out. wget: unable toresolve host address download.bt.cn’ 二、解决: 第一步:如下命令执行拿到返回的I…...

问:Redis常见性能问题及解法?
Redis 作为一个高性能的键值存储系统,在实际应用中可能会遇到各种性能问题。本文将探讨 Redis 的常见性能问题,并提供相应的解决建议。主要针对五个关键问题进行讨论:Master 节点的持久化工作、Slave 节点的数据备份、主从复制的网络环境、主…...

Imperva 数据库与安全解决方案
Imperva是网络安全解决方案的专业提供商,能够在云端和本地对业务关键数据和应用程序提供保护。公司成立于 2002 年,拥有稳定的发展和成功历史并于 2014 年实现产值1.64亿美元,公司的3700多位客户及300个合作伙伴分布于全球各地的90多个国家。…...

【JavaScript】之文档对象模型(DOM)详解
JavaScript 的强大之处在于它能够与 HTML 和 CSS 交互,动态地修改网页内容和样式。而实现这一功能的核心就是 DOM(文档对象模型)。 一、什么是 DOM? DOM 是文档对象模型(Document Object Model)的缩写。它…...

速盾:cdn域名与ip区别
CDN(内容分发网络)是一种通过在全球多个服务器上缓存和分发静态资源的网络服务,可以提高网站的访问速度和性能。在使用CDN时,域名与IP地址是两个关键的概念。本文将介绍CDN域名与IP地址的区别和作用。 首先,CDN域名是…...

如何优雅的在页面上嵌入AI-Agent人工智能
前言 IDEA启动!大模型的title想必不用我多说了,多少公司想要搭上时代前言技术的快车,感受科技的魅力。现在大模型作为降本增效的强大工具,基本上公司大多人都想要部署开发一把,更多的想要利用到这些模型放到生产中来提…...
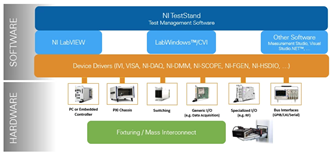
如何对LabVIEW软件进行性能评估?
对LabVIEW软件进行性能评估,可以从以下几个方面着手,通过定量与定性分析,全面了解软件在实际应用中的表现。这些评估方法适用于确保LabVIEW程序的运行效率、稳定性和可维护性。 一、响应时间和执行效率 时间戳测量:使用LabVIEW的时…...

动态规划 —— dp问题-按摩师
1. 按摩师 题目链接: 面试题 17.16. 按摩师 - 力扣(LeetCode)https://leetcode.cn/problems/the-masseuse-lcci/description/ 2. 算法原理 状态表示:以某一个位置为结尾或者以某一个位置为起点 dp[i]表示:选择到i位置…...

SQL 语法学习
在当今数字化的时代,数据的管理和分析变得至关重要。而 SQL(Structured Query Language),即结构化查询语言,作为一种用于管理关系型数据库的强大工具,掌握它对于从事数据相关工作的人来说是一项必备技能。在…...

MYSQL---TEST5(Trigger触发器Procedure存储过程综合练习)
触发器Trigger 数据库mydb16_trigger创建 表的创建 goods create table goods( gid char(8) primary key, #商品号 name varchar(10), #商品名 price decimal(8,2), #价格 num int;) #数量orders create tabl…...

蓝桥杯 区间移位--二分、枚举
题目 代码 #include <stdio.h> #include <string.h> #include <vector> #include <algorithm> #include <iostream> using namespace std; struct node{ int a,b; }; vector<node> q; bool cmp(node x,node y){ return x.b <…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
