【算法】Floyd多源最短路径算法
目录
一、概念
二、思路
三、代码
一、概念
在前面的学习中,我们已经接触了Dijkstra、Bellman-Ford等单源最短路径算法。但首先我们要知道何为单源最短路径,何为多源最短路径
- 单源最短路径:从图中选取一点,求这个点到图中其他节点的最短路径
- 多源最短路径:从图中任选两个节点,我们都能知道这两点间的最短路径
Floyd多源最短路径算法可用于求图中任意两点间的最短路径长,其核心思路在于依次将每个节点作为路径的中间点来更新其他任意两点的较优解,最后得到全局最优解
二、思路
1.首先我们需要一个图,和二维数组g、path

其中:
- g用于存储从i到j的最短路径长度
- path用于存储从i到j的最短路径的终点 的 前继节点
例如初始时,从1到2的最短路径就是权重为6的边,其终点为2,而对于这条路径而言2的前继节点为1,因此path[1][2] = 1
g(0)和path(0)意为矩阵g和path的初始态。因为初始时两个节点之间的最短路径就是他们之间的边,因此我们在初始化这两个数组时,只需要按照样例输入的边填写矩阵g即可
若从i到j之间没有边,则填最大值即可,例如g[3][2] = MAX,因为没有从3指向2的边
而矩阵path在初始化时按照上面的规则初始化即可,例如初始从3到1的最短路径就是3->1,终点为1,前继节点为3,因此path[3][1] = 3
2. 从1号节点开始,将每个节点作为任意两个节点的最短路径的中间点
有的人听到这里可能已经懵了,我们跟着图慢慢走

此时g(0)、path(0)变为g(1)和path(1),代表接下来要更新 i->1->j 的最短路径
但是我们并不需要将矩阵g和矩阵path中的所有值都更新,例如g[1][2],判断1->1->2的路径是否比1->2的最短路径更短是不具有价值的。两个矩阵中,如果行标和中间节点一样、列标和中间节点一样或者行标和列标一样的话,我们直接跳过即可
因此,只有2->1->3的情况,和3->1->2的情况需要讨论

(带虚线的位置代表不需要判断)
可以看到,2->1->3的距离为2->1的最短距离加1->3的最短距离,即g[2][1]+g[1][3] = 23,这个距离并不比g[2][3]小,因此不需要更新
而3->1->2的距离为11,小于原来的值MAX,因此更新,同时path[3][2]也更新为3->1->2的终点的前继节点即1
3.重复第二步直到所有节点都已作为中间点

1->2->3的距离为g[1][2]+g[2][3] = 10,比原来的13更小,因此将g[1][3]更新,path[1][3] = 2
3->2->1的距离为g[3][2]+g[2][1] = 21,比g[3][1]大,不更新

1->3->2的距离为21,比g[1][2]大,不更新
2->3->1的距离为g[2][3]+g[3][1] = 9,比原来的10更小,因此将g[2][1]更新,path[2][1] = 3
至此,我们就得到了图中任意两点间的最短路径长度了
而最短路径本身,则可以根据矩阵path中的值推出来,例如要求从2到1的最短路径,首先知道终点为节点1,根据path[2][1]知道下一个节点3,再根据path[2][3]知道下一个节点2,最后path[2][2]为-1说明路径走到结尾,因此完整的最短路径就为2->3->1
三、代码

#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug(x) cout << #x << " = " << x << '\n'
#define INF 0x3f3f3f3f
using namespace std;#define N 210
#define M 20010int n, m, k;
int g[N][N]; //存储从i到j的最短路径长度
int path[N][N] = {-1}; //path[i][j]存储从i到j最短路径的终点 的 前继节点void Floyd()
{for(int i = 1; i <= n; i++){g[i][i] = 0; //自己到自己的路径长度设置为0path[i][i] = -1; //自己到自己的路径设置为-1}for(int k = 1; k <= n; k++) //代表从i经过k到j的最短路径{for (int i = 1; i <= n; i++) //第i行{for (int j = 1; j <= n; j++) //第j列{if(i == j || i == k || j == k) //多余情况continue;if(g[i][k] + g[k][j] < g[i][j]) //从i经过k到j的最短路径 比 原先从i到j的最短路径更短{g[i][j] = g[i][k] + g[k][j]; //更新从i到j的最短路径path[i][j] = path[k][j]; //更新从i到j最短路径的终点 的 前继节点}}}}
}void solve()
{memset(g, 0x3f, sizeof g);cin >> n >> m >> k;for(int i = 0;i < m; i++){int a, b, w;cin >> a >> b >> w;g[a][b] = min(g[a][b], w); //可能存在重边path[a][b] = a; //初始时从a到b最短路径终点的前继节点就是a本身}Floyd(); //Floyd算法for (int i = 0; i < k; i++){int a, b;cin >> a >> b;if(g[a][b] > INF / 2)cout << "impossible" << endl;elsecout << g[a][b] << endl;}
}signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t = 1;//cin >> t;while(t--)solve();return 0;
}完.
相关文章:

【算法】Floyd多源最短路径算法
目录 一、概念 二、思路 三、代码 一、概念 在前面的学习中,我们已经接触了Dijkstra、Bellman-Ford等单源最短路径算法。但首先我们要知道何为单源最短路径,何为多源最短路径 单源最短路径:从图中选取一点,求这个点到图中其他…...

iOS SmartCodable 替换 HandyJSON 适配记录
前言 HandyJSON群里说建议不要再使用HandyJSON,我最终选择了SmartCodable 来替换,原因如下: 首先按照 SmartCodable 官方教程替换 大概要替换的内容如图: 详细的替换教程请前往:使用SmartCodable 平替 HandyJSON …...
)
使用 axios 拦截器实现请求和响应的统一处理(附常见面试题)
在现代前端开发中,我们经常需要向服务器发送 HTTP 请求,并根据响应内容做不同的处理。axios 是一个流行的 HTTP 库,提供了 拦截器 功能,可以在请求和响应阶段插入自定义逻辑,这使得我们在处理认证、错误提示等场景时更…...
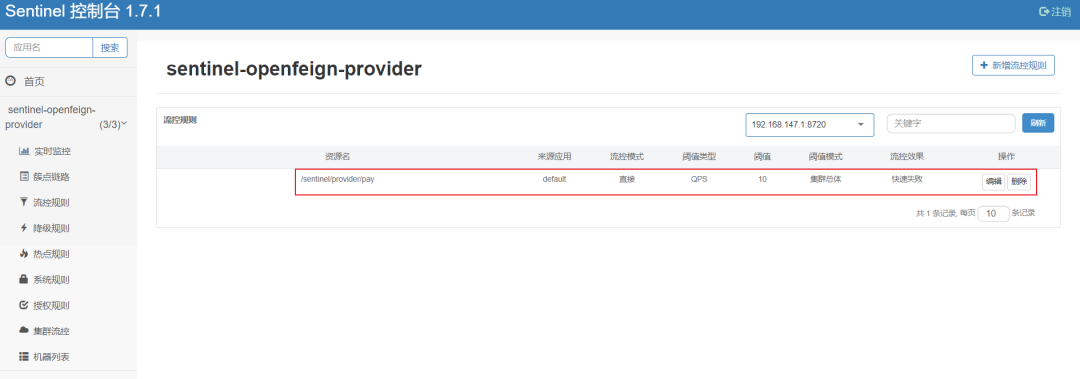
阿里 Sentinel
1、什么是sentinel? sentinel顾名思义:卫兵;在Redis中叫做哨兵,用于监控主从切换,但是在微服务中叫做流量防卫兵。 Sentinel 以流量为切入点,从流量控制、熔断降级、系统负载保护等多个维度保护服务的稳定…...

【点云网络】 pointnet 和 pointnet++
这两个网络都是斯坦福大学的一个团队提出的 我先先看一下pointnet的网络架构,这个网络比较经典,是2016年提出的: PointNet 是一个专门用于点云数据处理的神经网络。它的设计目的是直接操作不规则的点云数据,而无需将点云数据转换为规则网格或…...

.net core mvc 控制器中页面跳转
方式一: 在控制器的方法内部结尾使用 return View(); 来打开与方法同名的页面,如: public ActionResult Login() { return View(); } 该写法打开 Login 页面。 方式二: 可以添加参数来显式地指定要跳转的页面࿰…...

大学适合学C语言还是Python?
在大学学习编程时,选择C语言还是Python,这主要取决于你的学习目标、专业需求以及个人兴趣。以下是对两种语言的详细比较,帮助你做出更明智的选择: C语言 优点: 底层编程:C语言是一种底层编程语言&#x…...

跳表原理课堂笔记
课程地址 跳表是一种基于随机化的有序数据结构,它提出是为了赋予有序单链表以 O(logn) 的快速查找和插入的能力 创建 首先在头部创建一个 sentinel 节点,然后在 L1 层采用“抛硬币”的方式来决定 L0 层的指针是否增长到 L1 层 例如上图中,L…...

Windows系统使用OpenSSL生成自签名证书
Nginx服务器添加SSL证书。 要在Windows系统的Nginx Web服务器上使用OpenSSL生成证书,并确保该证书能在局域网内被计算机信任,你可以按照以下详细步骤进行操作: 一、生成证书 下载并安装OpenSSL: 从OpenSSL的官方网站下载适用于Wi…...

定位new的表达式
这里面会涉及内存池,所谓的内存池就是池化技术,让我们使用的更加方便,里面有1.线存池和连接池。 如果想要高频释放内存池,要针对系统有个堆,而堆事针对我们需要的生擒一个特例,和我们家庭里面妈妈给爸爸的…...

矩阵特殊打印方式
小伙伴们大家好,好几天没更新了,主要有个比赛。从今天起继续给大家更新,今天给大家带来一种新的题型:矩阵特殊打印方式。 螺旋打印矩阵 解题思路 首先给大家看一下什么是螺旋方式打印: 就像这样一直转圈圈。 我想大多…...

OCC 拟合的平面转换为有界平面
问题:针对导入的部分面无法获取大小,同时也无法判断点是否在面上。但是OBB可以获取大小 解决方法:通过面拟合转换gp_Pln,然后获取面的内外边,重新修剪生成新的TopoDS_Face 疑问:本人对OCC中各种面的特性不…...

Nginx性能优化的几个方法
文章目录 一 Nginx 配置优化二 缓存利用三 压缩策略四 安全性优化修改配置文件修改 Nginx 源码使用第三方模块 五 监控和日志优化六 系统层面优化七 故障转移优化 小伙伴们平时使用 Nginx 是否有进行过性能优化呢?还是软件装好了就直接使用呢? 今天松哥和…...

Unity性能优化5【物理篇】
1.刚体的碰撞检测属性首选离散型 离散碰撞的缺点是小物体快速移动时,有丢失碰撞的风险。此下拉菜单中,越下面的选项碰撞检测频率越高,性能消耗也显著增加。因此在选择碰撞检测类型时尽量选择离散型。 2.优化碰撞矩阵 合理标记碰撞矩阵可以减…...

我的工具列表
开发工具 名称备注Visual Studio微软开发工具集Visual Studio Code代码编辑器Qt CreatorQt IDEQt Design StudioQt 界面设计器linguistQt 国际化翻译PyCharmPython IDEVMware Workstation Pro虚拟机MATLAB数据计算和仿真Keil单片机 IDENavicat Premium数据库管理MobaXterm远程…...

985研一学习日记 - 2024.11.5
一个人内耗,说明他活在过去;一个人焦虑,说明他活在未来。只有当一个人平静时,他才活在现在。 日常 1、起床6:00 2、健身1.5h 今天练了胸,然后跑了会步,又吃多了,明天少吃点! 3、…...

Vue2 与 Vue3 的区别
Vue.js 作为流行的前端框架,已经经历了多次版本的更新迭代,从 Vue2 到 Vue3 的转变不仅带来了新的功能,也在性能、开发体验等方面作出了显著改进。无论是对于新手还是有经验的开发者,了解这两个版本之间的差异都至关重要。本文将讨…...

虚拟现实技术课程开发思路
文章目录 组队选题立项分工建模说明:场景说明:交互说明: 结语: 前言:最近学弟学妹们反馈水水老师课程开始上强度了。不仅有翻转课堂,还有理论课实验课都要做东西出来。听说理论课是做什么博物馆什么的&…...

triangle_area_calculators库发布
最近将在pip网站上发布triangle_area_calculators库(我编写的python第三方库) triangle_area_calculators库用于计算不同类型及不同已知量的三角形面积 在triangle_area_calculators库中,有一个名为TriangleAreaCalculators的类 可以通过f…...

ClickHouse数据库SSL配置和SSL连接测试
目录 1.Server SSL配置介绍 2.Client SSL访问配置的介绍 3.my测试环境上开启ClickHouse Server SSL配置 & 客户端SSL访问的配置流程 4.附录 1)SSL证书的几种类型 单域名SSL证书 通配符SSL证书 多域名SSL证书 多域名通配符SSL证书 2)单域名…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
