leetcode哈希表(五)-四数相加II
题目
454.四数相加II
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
0 <= i, j, k, l < nnums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
示例 1:
输入:nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2] 输出:2 解释: 两个元组如下: 1. (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0 2. (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0
示例 2:
输入:nums1 = [0], nums2 = [0], nums3 = [0], nums4 = [0] 输出:1
思路
首先想到的是暴力法,四个循环,但复杂度为n的四次方。
由题目中
nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0可知,可将四个数组分成两组
nums1[i] + nums2[j] == -(nums3[k] + nums4[l])
先遍历nums1和nums2,求出各个和,用哈希表存储,再去后两组数组中看是否存在相反数
代码
class Solution:def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:count = 0dict1 ={}for n1 in nums1:for n2 in nums2:if n1+n2 not in dict1:dict1[(n1+n2)] = 1else:dict1[(n1+n2)] += 1for n3 in nums3:for n4 in nums4:if -(n3+n4) in dict1:count += dict1[(-(n3+n4))]return count相关文章:
-四数相加II)
leetcode哈希表(五)-四数相加II
题目 454.四数相加II 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < nnums1[i] nums2[j] nums3[k] nums4[l] 0 示例 1: 输入&…...

Java学习路线:Maven(一)认识Maven
目录 认识Maven 新建Maven文件 导入依赖 认识Maven Maven是一个Java的项目管理工具,通过Maven,我们可以实现: 项目自动构建,包括代码的编译、测试、打包、安装等依赖管理,快速完成依赖的导入 在学习Maven之前&…...

【深度学习】— 多输入多输出通道、多通道输入的卷积、多输出通道、1×1 卷积层、汇聚层、多通道汇聚层
【深度学习】— 多输入多输出通道、多通道输入的卷积、多输出通道、11 卷积层、汇聚层、多通道汇聚层 多输入多输出通道多通道输入的卷积示例:多通道的二维互相关运算 多输出通道实现多通道输出的互相关运算 11 卷积层11 卷积的作用 使用全连接层实现 11 卷积小结 …...

java mapper 的 xml讲解
<?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE mapper PUBLIC "-//mybatis.org//DTD Mapper 3.0//EN" "http://mybatis.org/dtd/mybatis-3-mapper.dtd"> <mapper namespace"com.bnc.s12.mapper.GoodaCateDT…...

全面解析:区块链技术及其应用
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 全面解析:区块链技术及其应用 文章目录 全面解析:区块链技术及其应用什么是区块链区块链的工作原理1. 分…...

python基础学习笔记
本文类比c语言讲解python 一.变量和类型 前缀小知识: 注意:1.python写每一行代码时,结尾不需要 ; 这点是和c语言有很大区别的 2.代码的缩进(就是每行代码前面的空格)是非常重要的后文会提到 1.定义变量 注意: 和C/C …...

【dvwa靶场:XSS系列】XSS (DOM) 低-中-高级别,通关啦
一、低级low 拼接的url样式: http://127.0.0.1/dvwa/vulnerabilities/xss_d/?default 拼接的新内容 <script>alert("假客套")</script> 二、中级middle 拼接的url样式: http://127.0.0.1/dvwa/vuln…...

ONLYOFFICE 8.2深度体验:高效协作与卓越性能的完美融合
📝个人主页🌹:Eternity._ 🌹🌹期待您的关注 🌹🌹 ❀ONLYOFFICE 8.2 🔍引言📒1. ONLYOFFICE 产品简介📚2. 功能与特点🍁协作编辑 PDF🍂…...

Mac如何将多个pdf文件归并到一个
电脑:MacBook Pro M1 操作方式: very easy 选中想要归并的所有pdf文件,然后 右键 -> quick actions -> Create PDF 然后就可以看到将所选pdf文件归并为一个pdf的文件了...

LINUX下的Mysql:Mysql基础
目录 1.为什要有数据库 2.什么是数据库 3.LINUX下创建数据库的操作 4.LINUX创建表的操作 5.SQL语句的分类 6.Mysql的架构 1.为什要有数据库 直接用文件直接存储数据难道不行吗?非得搞个数据库呢? 首先用文件存储数据是没错,但是文件不方…...

自然语言处理方向学习建议
自然语言处理方向学习建议 自然语言处理(NLP)作为人工智能的一个重要分支,近年来在学术界和工业界都取得了显著的发展。作为即将或正在攻读博士学位的你,投身于NLP领域无疑是一个充满挑战与机遇的选择。以下是一些针对NLP方向学习…...

介绍一下如何生成随机数(c基础)
适合对象 c语言初学者 总结语言用色,个人强调用红色,注意为易错点,若有问题请告诉我谢谢。(建议通过目录观看)。一定要自己动手打代码。 rand函数 是生成随机数的函数,但实则是伪随机数。(即是同一个值) 格式 #include<st…...

24-11-1-读书笔记(三十一)-《契诃夫文集》(五)下([俄] 契诃夫 [译] 汝龙)生活乏味但不乏魅力。
文章目录 《契诃夫文集》(五)下([俄] 契诃夫 [译] 汝龙)生活乏味但不乏魅力。目录阅读笔记总结 《契诃夫文集》(五)下([俄] 契诃夫 [译] 汝龙)生活乏味但不乏魅力。 休息,…...

从“点”到“面”,热成像防爆手机如何为安全织就“透视网”?
市场上测温产品让人眼花缭乱,通过调研分析,小编发现测温枪占很高比重。但是,测温枪局限于显示单一数值信息,无法直观地展示物体的整体温度分布情况,而且几乎没有功能拓展能力。以AORO A23为代表的热成像防爆手机改变了…...

基于vue框架的的奶茶店预约订单系统3fb55(程序+源码+数据库+调试部署+开发环境)系统界面在最后面。
系统程序文件列表 项目功能:用户,奶茶分类,奶茶信息 开题报告内容 开题报告 题目:基于Vue框架的奶茶店预约订单系统开发 一、研究背景与意义 背景 随着饮品市场的蓬勃发展,奶茶店作为其中的重要组成部分,其业务量和顾客需求持…...

项目实战使用gitee
1.创建本地仓库 2.进行提交到本地仓库 创建仓库后在idea中会显示图标,点击绿色的√进行快速提交 3.绑定远程仓库 4.番外篇-创建gitee仓库 注意不要勾选其他...

数据结构--二叉树_链式(下)
实现链式结构二叉树 链式结构就是由一个一个的节点组成。 ⽤链表来表⽰⼀棵⼆叉树,即⽤链来指⽰元素的逻辑关系。 通常的⽅法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别⽤来给出该结点左孩⼦和右孩⼦所在的链结点的存储…...

unity游戏开发之--人物打怪爆材料--拾进背包的实现思路
unity游戏开发之–人物打怪爆材料–拾进背包的实现思路 游戏实现:unity c# 1、敌人(怪物)的生命值和伤害系统 using UnityEngine; using System.Collections.Generic;public class Enemy : MonoBehaviour {[Header("基础属性")]…...

AWTK文件系统适配器更新-支持RT-Thread DFS POSIX接口
介绍 AWTK 文件系统适配器。 在嵌入式平台中,有时没有 POSIX 兼容的文件系统 API,需要把一些文件系统实现,包装成 AWTK 的 fs 接口。本项目提供一些常见文件系统的适配,目前支持的文件系统有: FATFS 主要用于访问 TF…...
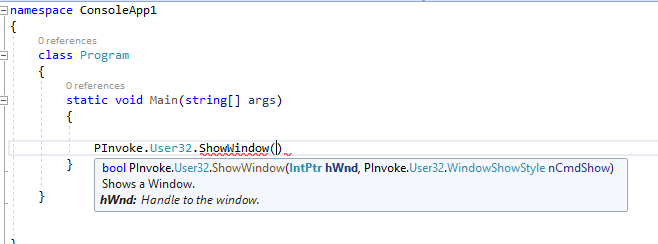
C#如何快速获取P/Invoke方法签名
使用API函数已经好几年了,封装函数签名基本是参照MSDN上的文档,然后再做数据类型对应。 虽然有 pinvoke.net 这个网站,但基本很少使用。一方面是想多动手,另一方面是因为各种数据类型基本都用过了,都能自己在C#中 对应…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
