【5.10】指针算法-快慢指针将有序链表转二叉搜索树
一、题目
-10 5
二、解题思路
二叉搜索树具有这样的特点:当前节点大于左子树的所有节点,同时小于右子树的所有节点,并且每个节点都具备这个特性。
题中提到,是按照升序排列的单链表,我们只需找到链表的中间节点,使其成为树的根节点。中间节点前面的部分就是根节点左子树的所有节点,中间节点后面的部分就是根节点右子树的所有节点。然后,使用递归的方式再分别对左右子树进行相同的操作……
这里以链表 1→2→3→4→5 为例来画个图看一下。

三、代码实现
#include <iostream>
#include <vector>
#include <queue>// 定义链表节点
struct ListNode {int val;ListNode* next;ListNode(int x) : val(x), next(nullptr) {}
};// 定义树节点
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 将有序链表转换为二叉搜索树
TreeNode* sortedListToBST(ListNode* head) {// 边界条件的判断if (head == nullptr)return nullptr;if (head->next == nullptr)return new TreeNode(head->val);// 通过快慢指针找到链表的中间结点slow,pre就是中间结点slow的前一个结点ListNode* slow = head;ListNode* fast = head;ListNode* pre = nullptr;while (fast != nullptr && fast->next != nullptr) {pre = slow;slow = slow->next;fast = fast->next->next;}// 链表断开为两部分,一部分是node的左子节点,一部分是node的右子节点pre->next = nullptr;// node就是当前节点TreeNode* node = new TreeNode(slow->val);// 从head节点到pre节点是node左子树的节点node->left = sortedListToBST(head);// 从slow.next到链表的末尾是node的右子树的结点node->right = sortedListToBST(slow->next);return node;
}// 打印树的层序遍历结果
void printTreeLevelOrder(TreeNode* root) {if (root == nullptr)return;std::queue<TreeNode*> q;q.push(root);bool first = true;while (!q.empty()) {int size = q.size();for (int i = 0; i < size; ++i) {TreeNode* node = q.front();q.pop();if (!first) {std::cout << ", ";}first = false;if (node != nullptr) {std::cout << node->val;q.push(node->left);q.push(node->right);} else {std::cout << "null";}}}std::cout << std::endl;
}// 创建链表
ListNode* createLinkedList(const std::vector<int>& values) {ListNode* dummy = new ListNode(0);ListNode* current = dummy;for (int val : values) {current->next = new ListNode(val);current = current->next;}return dummy->next;
}int main() {// 输入给定的有序链表:[-10, -3, 0, 5, 9]std::vector<int> values = {-10, -3, 0, 5, 9};ListNode* head = createLinkedList(values);// 将有序链表转换为二叉搜索树TreeNode* root = sortedListToBST(head);// 打印树的层序遍历结果std::cout << "[";printTreeLevelOrder(root);std::cout << "]" << std::endl;return 0;
}相关文章:

【5.10】指针算法-快慢指针将有序链表转二叉搜索树
一、题目 给定一个单链表,其中的 元素按升序排序 ,将其转换为 高度平衡的二叉搜索树 。 本题中,一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。 示例: 给定的有序链表: [ -10 , -3 , 0 , …...

机器学习—前向传播的一般实现
可以写一个函数来实现一个密集的层,那是神经网络的单层,所以定义稠密函数,它将上一层的激活作为输入以及给定层神经元的参数w和b。看下边图片所展示的例子,把所有这些权重向量堆叠成一个矩阵,wnp.array([[1,-3,5][2,4,…...

极狐GitLab 签约足下科技,加速国产智驾操作系统的发展与普及
客户背景 足下科技是一家致力于成为智能汽车软件平台、产品与服务领导者的高科技企业,成立于 2022年 3 月,总部位于深圳市。足下科技自主研发的智能驾驶操作系统 Earth 和 Air 工具链,协助OEM和Tier1厂商降低算法和软件开发难度,…...

20241102在荣品PRO-RK3566开发板的预置Android13下适配宸芯的数传模块CX6603N
20241102在荣品PRO-RK3566开发板的预置Android13下适配宸芯的数传模块CX6603N 2024/11/2 18:04 在WIN10使用程序:ViewLink-4.0.7_0708-windows-x64.exe 在荣品PRO-RK3566开发板的预置Android13下使用:ViewLink-2023_12_21-release-0.2.6.apk adb install…...

力扣(leetcode)题目总结——哈希表篇
leetcode 经典题分类 链表数组字符串哈希表二分法双指针滑动窗口递归/回溯动态规划二叉树辅助栈 本系列专栏:点击进入 leetcode题目分类 关注走一波 前言:本系列文章初衷是为了按类别整理出力扣(leetcode)最经典题目,…...

AWS RDS Oracle hit ORA-39405
报错信息: ORA-39405: Oracle Data Pump does not support importing from a source database with TSTZ version 42 into a target database with TSTZ version 35. 分析过程: 这个报错是由于timezone_file的版本,源端比目标端高…...

Dinky中配置Flink集群
需要启动yarn-session 进程,在集群服务器 cd /pwd//flink/bin yarn-session -d 启动成功后可以在yarn的资源管理队列进行查看 启动成功后会给出:JobManager Web Interface 在dinky中进行配置: 集群配置 Hadoop 配置: H…...

通讯录(C 语言)
目录 一、通讯录设计思路1. 伪代码设计思路2. 代码设计思路 二、代码实现三、程序运行演示四、整体分析 一、通讯录设计思路 1. 伪代码设计思路 通讯录可以用来存储 100 个人的信息,每个人的信息包括:姓名、性别、年龄、电话、住址。 提供方法&#x…...

对比Java和TypeScript中的服务注册和查找机制
文章目录 一、Java中的服务注册和查找二、TypeScript中的服务注册和查找2.1 使用依赖注入(DI)框架2.2 injectable原理2.3 使用TypeScript的反射系统实现依赖注入 三、优缺点分析3.1 Java的ServiceLoader3.2 TypeScript的服务注册和查找 四、结论 在构建大…...

Flutter 主流常用第三方库、插件收集
一、Flutter 学习资料 FlutterFlutter官网Flutter中文网咸鱼技术掘金Flutter专栏 Flutter - Dart中(.)、(..)、(...)语法使用_flutter ...-CSDN博客 Flutter pubspec.yaml 配置文件_flutter yaml配置git-CSDN博客 Flutter 添加 example流程_建flutter 工程 怎么自动有example-C…...

【在Linux世界中追寻伟大的One Piece】多路转接select
目录 1 -> I/O多路转接之select 1.1 -> 初识select 1.2 -> select函数原型 1.3 -> 关于fd_set结构 1.4 -> 关于timeval结构 2 -> 理解select执行过程 2.1 -> Socket就绪条件 2.2 -> select特点 2.3 -> select缺点 3 -> select使用示例…...

补一下 二维 平面直角坐标系 到三维
上一篇帖子写到 二维的平面直角坐标系,是那样的,这次补充一下三维的。首先需要,安装一个包,如下: 然后,把参数输入,输入这个坐标系的参数,如下: 这样就可以输出如下的三…...

如何学习Python编程?
如何学习Python编程? 了解基础概念: 学习Python的基本语法,包括变量、数据类型、运算符等。了解控制结构,如条件语句(if语句)和循环(for和while循环)。 选择学习资源: 在…...
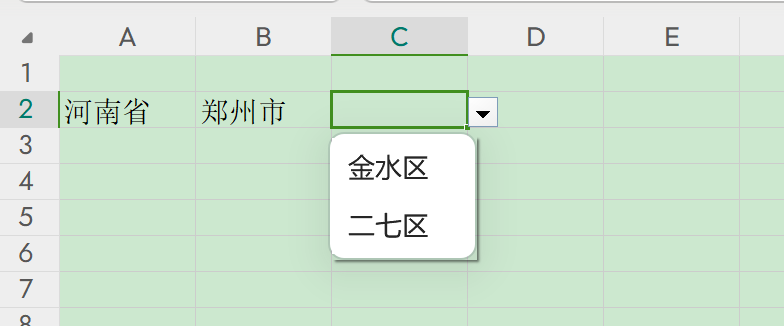
使用EasyExcel实现导出excel文件时生成多级下拉选
前言 公司有个需求本来只涉及到两个下拉选项,后面就想能不能实现多个下拉选,当然我这里说的多个下拉选是联动的,比如省、地市、区县这种。 实现步骤 1、添加EasyExcel的Maven依赖 <dependency><groupId>com.alibaba</group…...

微信小程序 高校教材征订系统
文章目录 项目介绍具体实现截图技术介绍mvc设计模式小程序框架以及目录结构介绍错误处理和异常处理java类核心代码部分展示详细视频演示源码获取 项目介绍 系统分为三个角色,分别是教材科、系教学秘书、教研室主任。系统主要完成功能是教材科要发布教材征订信息&am…...

从0开始的STM32 定时器(I):聊一聊基本定时器
目录 时钟源 控制器 时基单元 关于HAL库如何配置基本定时器 HAL是如何初始化我们的定时器句柄的 HAL_TIM_Base_Init 开始定时 如何处理句柄? 在我们使用STM32解决一些问题的时候,常常会遇到说:我想要以一个周期做一些事情:…...

vue常见题型(1-10)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 2.2双向绑定的原理是什么vue框架采用的是数据双向绑定的方式,由三个重要部分构成2.2.1.ViewModel2.2.2 双向绑定2.2.3.1.编译Compile2.2.3.2.依赖收集 3…...

【SpringBoot】使用注解进行XSS防御
在Spring Boot中,我们可以使用注解的方式来进行XSS防御。注解是一种轻量级的防御手段,它可以在方法或字段级别对输入进行校验,从而防止XSS攻击。 引入相关依赖 maven依赖: <!--JSR-303/JSR-380用于验证的注解 --> <de…...

华为海思招聘-芯片与器件设计工程师-模拟芯片方向- 机试题-真题套题题目——共8套(每套四十题)
华为海思招聘-芯片与器件设计工程师-模拟芯片方向- 机试题-真题套题题目分享——共九套(每套四十题) 岗位——芯片与器件设计工程师 岗位意向——模拟芯片 真题题目分享,完整题目,无答案(共8套) 实习岗位…...

vscode 下载慢的解决方法
下载链接示例:https://az764295.vo.msecnd.net/stable/ccbaa2d27e38e5afa3e5c21c1c7bef4657064247/code1.62.3-1637137107amd64.deb 解决方法: 把 az764295.vo.msecnd.net 替换成 vscode.cdn.azure.cn...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
