计算机网络——网络层导论




转发是局部功能——数据平面
路由是全局的功能——控制平面

网卡
网卡,也称为网络适配器,是计算机硬件中的一种设备,主要负责在计算机和网络之间进行数据传输。
一、主要功能
1、数据传输:
发送数据时,网卡将计算机内部的数据转换为网络信号,并通过网络线缆或无线信号发送出去。
接收数据时,网卡从网络中接收信号,将其转换为计算机可以识别的数据格式,并传递给操作系统和应用程序进行处理。
2、地址识别:
每张网卡都有一个唯一的物理地址(MAC 地址),用于在网络中标识该网卡。当数据在网络中传输时,网卡可以根据目的 MAC 地址判断该数据是否是发送给自己的。
3、协议处理:
网卡支持多种网络协议,如以太网协议、Wi-Fi 协议等。它负责根据协议的规定对数据进行封装和解封装,确保数据能够正确地在网络中传输。
二、类型
1、有线网卡:
通过以太网电缆连接到网络,通常用于台式计算机和服务器。有线网卡的传输速度较快,稳定性高,适用于对网络性能要求较高的场景。
2、无线网卡:
通过无线信号连接到网络,适用于笔记本电脑、平板电脑和智能手机等移动设备。无线网卡的便携性好,但传输速度和稳定性可能受到信号强度和干扰的影响。
sdn
sdn比传统的方式的区别,转发,block,泛洪,修改某些字段







相关文章:

计算机网络——网络层导论
转发是局部功能——数据平面 路由是全局的功能——控制平面 网卡 网卡,也称为网络适配器,是计算机硬件中的一种设备,主要负责在计算机和网络之间进行数据传输。 一、主要功能 1、数据传输: 发送数据时,网卡将计算机…...
` 方法更新数据库中的数据)
使用 JPA 的 `save()` 方法更新数据库中的数据
在开发基于 JPA(Java Persistence API)的应用时,数据持久化操作中的常见问题是执行 save() 方法后数据库中的数据没有更新。本文将详细介绍 JPA 的 save() 方法如何工作、其可能出现的问题,以及如何解决这些问题,以确保…...
Obsidian的Git插件设置配置全流程 -- 简单的电脑端多平台同步方案及常见问题
Obsidian的Git插件设置配置全流程 -- 简单的电脑端多平台同步方案及常见问题 参考文章引言1. git 介绍及安装2. git 本地配置及远程仓库链接3. obsidian 的 git 插件4. 常用的使用场景和对应的命令4.1. 本地仓库已推送到远端,如何在另一个电脑上第一次同步4.2 多端同…...
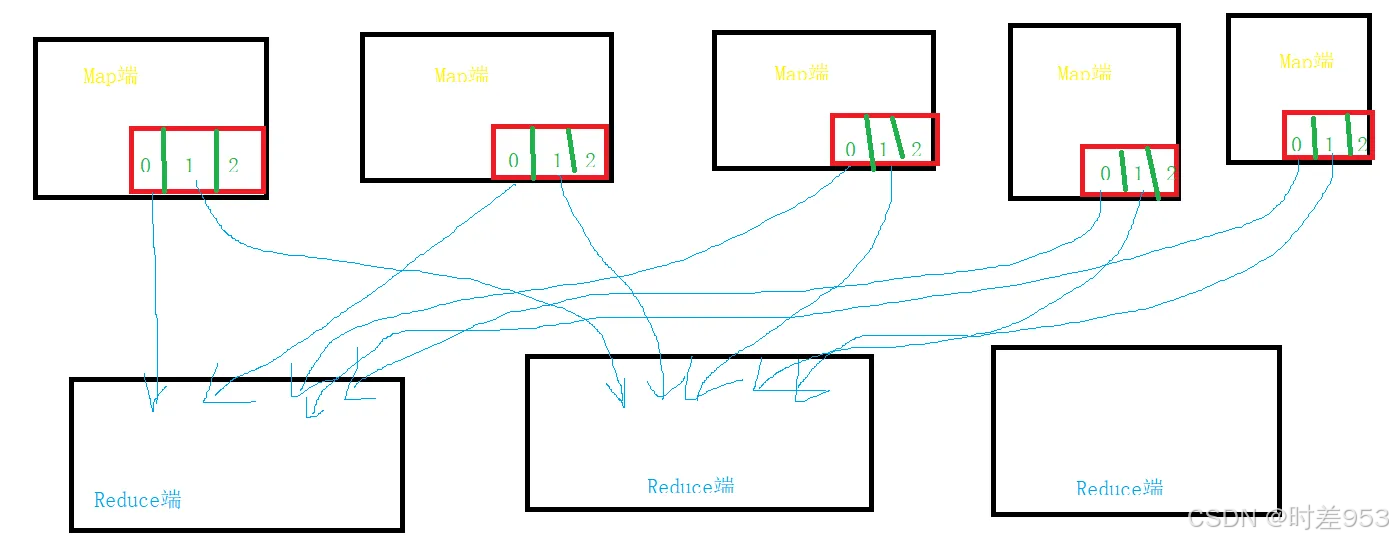
MapReduce 的 Shuffle 过程
MapReduce 的 Shuffle 过程指的是 MapTask 的后半程,以及ReduceTask的前半程,共同组成的。 从 MapTask 中的 map 方法结束,到 ReduceTask 中的 reduce 方法开始,这个中间的部分就是Shuffle。是MapReduce的核心,心脏。 …...

【Linux】进程控制——创建,终止,等待回收
目录 进程创建fork再介绍写时拷贝 进程终止退出码退出方式 进程等待获取子进程statuswaitwaitpid 在前两篇进程概念中,对进程进行了介绍,进行了初步认识,也认识到了与之相关联的进程地址空间;本文则对进程的生命周期——创建&…...

新手必看,17个常见的Python运行时错误
初入门的 Pythoner 在运行代码时免不了会遇到一些错误,刚开始可能看起来比较费劲。 随着代码量的积累,熟能生巧,当遇到一些运行时错误时能够很快的定位问题原题。 下面整理了常见的 17 个错误,希望能够帮助到大家。 1、忘记在 …...

pdf 添加页眉页脚,获取前五页
test /*** 加水印、页眉、页脚*/ Test void d1() throws IOException {//水印 样式调整String file "D:\\test\\2\\GB1.pdf";PdfUtil.WatermarkPDF(file); } /*** 获取前五页*/ Test void d2() throws IOException {String file "E:\\test\\2\\3.pdf";P…...
SQL 实战问题解析
在数据分析和数据库操作中,SQL 查询是至关重要的一环。本文将通过分析四道典型的 SQL 题目,深入探讨如何从复杂的业务需求中构建准确高效的 SQL 查询。 一、删除学生表冗余信息 需求解读 给定一个学生表,其中包含自动编号、学号、姓名、课程编…...
Android MVVM demo(使用DataBinding,LiveData,Fresco,RecyclerView,Room,ViewModel 完成)
使用DataBinding,LiveData,Fresco,RecyclerView,Room,ViewModel 完成 玩Android 开放API-玩Android - wanandroid.com 接口使用的是下面的两个: https://www.wanandroid.com/banner/jsonhttps://www.wan…...
python的安装环境Miniconda(Conda 命令管理依赖配置)
这一段时间,对AI大模型 有了兴趣就想研究一下。 在研究之前肯定要先把需要的编程技能掌握了。经过我查阅资料,今天就先学一下 python的 环境安装。 Node.js 包管理工具:npm 依赖配置文件:package.json 环境管理:nvm&am…...

【LeetCode】【算法】128. 最长连续序列
LeetCode 128. 最长连续序列 题目描述 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例: 输入:nums [10…...

【dvwa靶场:XSS系列】XSS (Reflected)低-中-高级别,通关啦
一、低级low 简单拿捏 <script>alert(123)</script>二、中级middle 源码过滤了script但是没有过滤大小写,改成大写S <Script>alert(123)</script>三、高级high 比中级高,过滤了script并且以及大小写,使用其他标…...
)
imu_tk配置教程(锁死ubuntu18.04,不要22.04)
在ubuntu18.04上安装。 imu_tk 的 cmake 必须要qt4.x,但 ubuntu22.04 和qt4.x不适配。 1、安装 ceres-solver 下载路径:http://ceres-solver.org/installation.html (需要梯子,核心内容记录如下。需下载 ceres-solver 安装包&am…...

Vue 的 keep-alive
什么是 keep-alive? <keep-alive> 是一个内置组件,用于缓存组件实例,从而提高应用的性能。当包裹动态组件时,<keep-alive> 会缓存不活跃的组件实例,而不是销毁它们。这使得当组件重新激活时,可…...

linux进程的状态之环境变量
我们在前面了解了进程的状态及相关概念 接下来我们接着上一篇进程的状态接着了解环境变量 进程的状态 文章目录 目录 文章目录 前言 二、环境变量 1、常见环境变量 2、查看环境变量 3、修改PATH 4、HOME 5、PATH 编辑 6、和环境变量相关的命令 三、环境变量的组织…...
)
【系统架构设计师】预测试卷一:论文(包括4篇论文主题对应的写作要点分析)
更多内容请见: 备考系统架构设计师-专栏介绍和目录 文章目录 试题一:论面向服务的架构设计与应用试题一写作要点试题二:论软件架构的脆弱性试题二 写作要点试题三:论分布式存储系统架构设计试题三 写作要点试题四:论网络安全体系架构设计及应用试题四 写作要点试题一:论面…...

东胜物流软件 AttributeAdapter.aspx SQL 注入漏洞复现
0x01 产品简介 东胜物流软件是青岛东胜伟业软件有限公司一款集订单管理、仓库管理、运输管理等多种功能于一体的物流管理软件。该公司初创于2004年11月(前身为青岛景宏物流信息技术有限公司),专注于航运物流相关环节的产品和服务。东胜物流信息管理系统货代版采用MS-SQLser…...
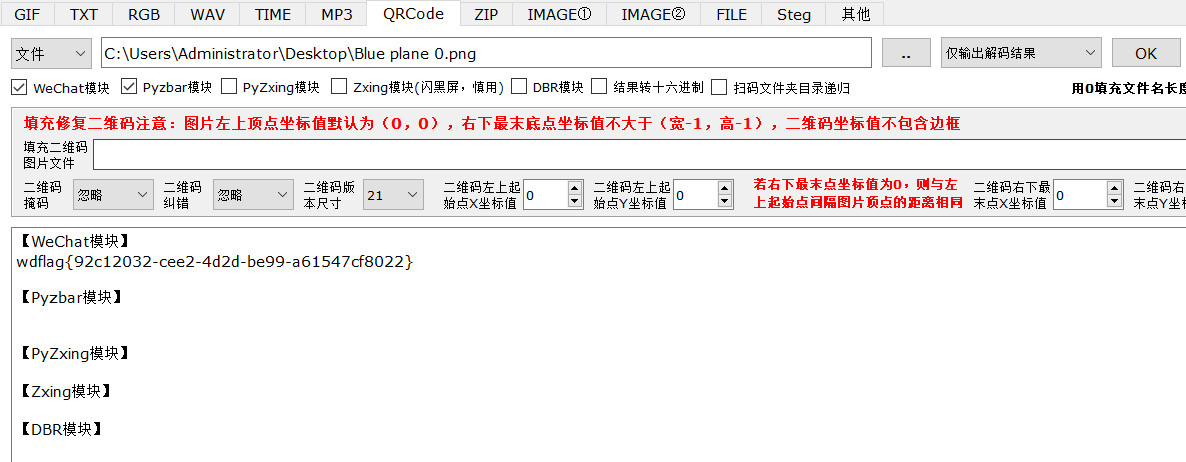
2024年网鼎杯青龙组|MISC全解
转载或摘抄时请标明出处 MISC01 wdbflag{22226aba1d98c4302a6f508cad7da5d8} MISC02 一把梭工具没有任何结果,估计缺少符号表,直接strings flag > out.txt导出后慢慢找线索 在桌面上发现了png和txt文件,用文件名做一次筛选 第一行发现bas…...

查询引擎的演变之旅 | OceanBase原理解读
在关系型数据库中,查询调度器与计划执行器,有着与查询优化器同样重要的地位,随着计算机硬件技术的飞速进步,这两大模块的重要性日益凸显,成为提升数据库性能的关键所在。接下来,本文将由来自 OceanBase 的技…...
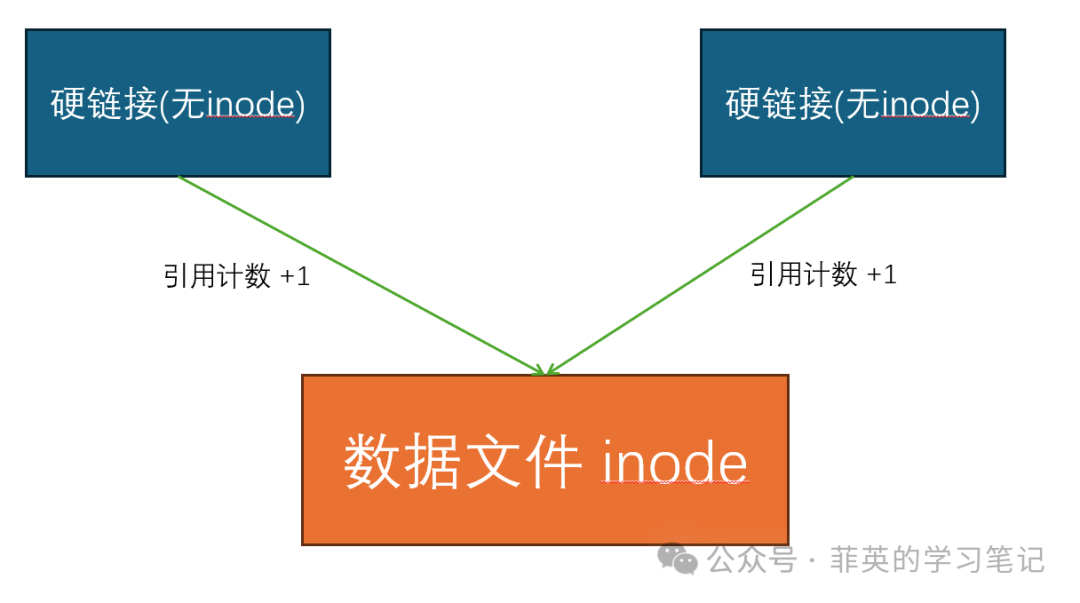
轻松理解操作系统 - Linux 软硬链接是什么?
Linux 由于其开源、比较稳定等特点统治了服务端领域。也因此,学习Linux 系统相关知识在后端开发等岗位中变得越来越重要,甚至可以说是必不可少的。 因为它的广泛应用,所以在程序员的日常工作和面试中,它都是经常出现的。它的开源特…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

Easy Excel
Easy Excel 一、依赖引入二、基本使用1. 定义实体类(导入/导出共用)2. 写 Excel3. 读 Excel 三、常用注解说明(完整列表)四、进阶:自定义转换器(Converter) 其它自定义转换器没生效 Easy Excel在…...
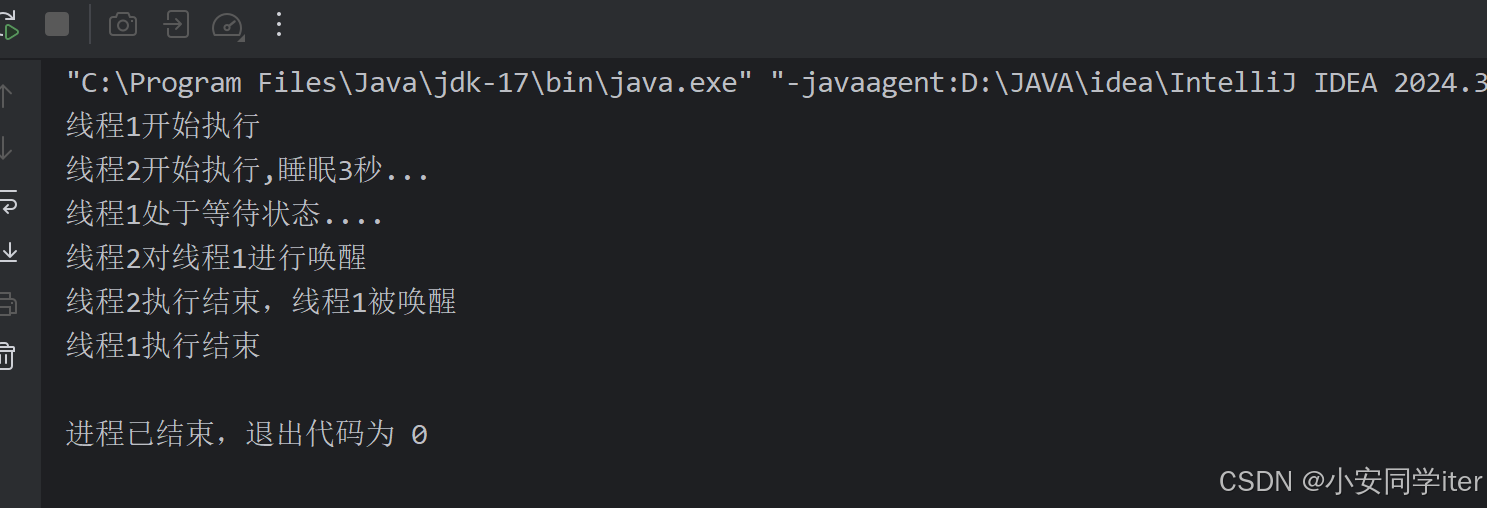
JUC并发编程(二)Monitor/自旋/轻量级/锁膨胀/wait/notify/锁消除
目录 一 基础 1 概念 2 卖票问题 3 转账问题 二 锁机制与优化策略 0 Monitor 1 轻量级锁 2 锁膨胀 3 自旋 4 偏向锁 5 锁消除 6 wait /notify 7 sleep与wait的对比 8 join原理 一 基础 1 概念 临界区 一段代码块内如果存在对共享资源的多线程读写操作…...
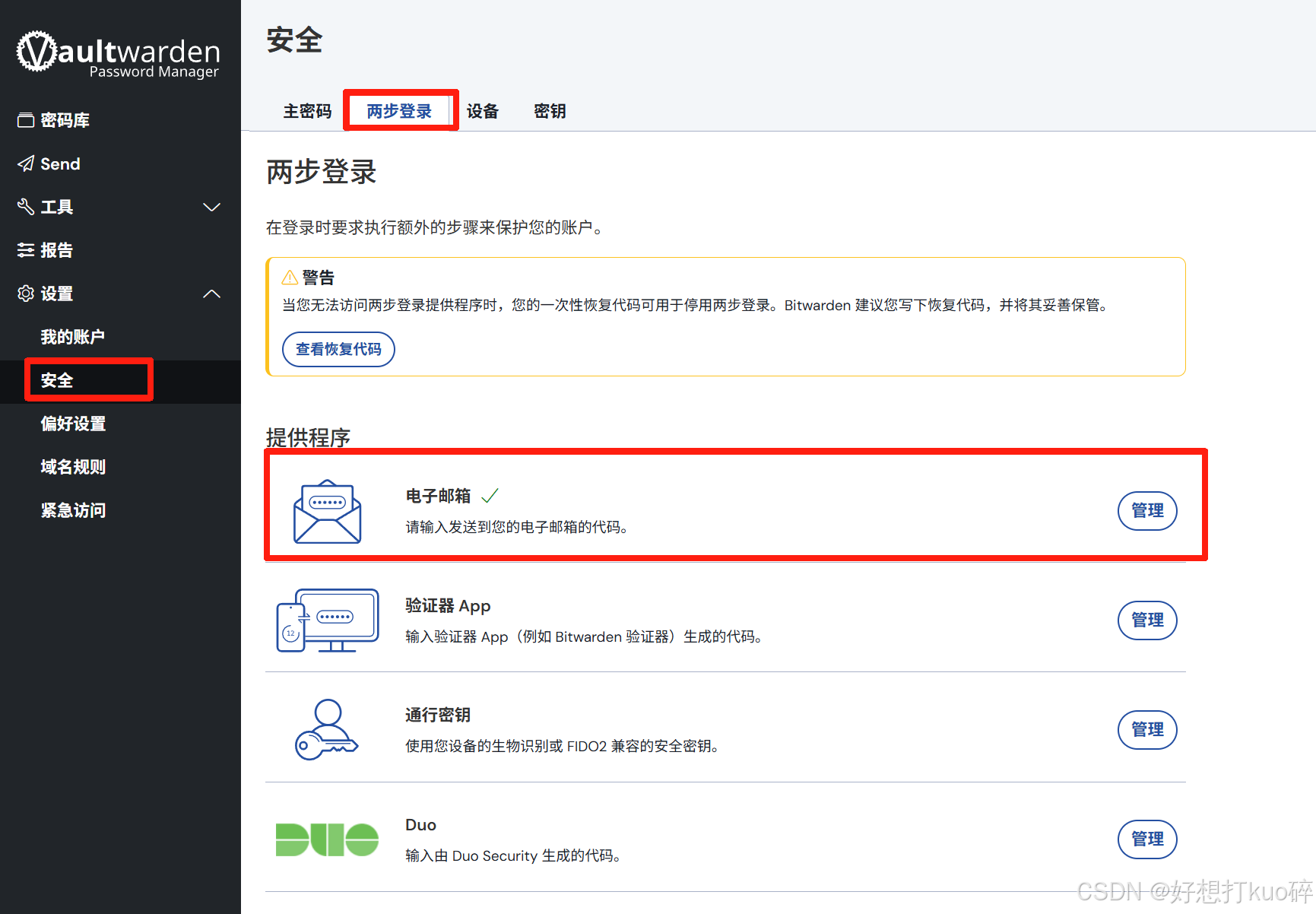
轻量安全的密码管理工具Vaultwarden
一、Vaultwarden概述 Vaultwarden主要作用是提供一个自托管的密码管理器服务。它是Bitwarden密码管理器的第三方轻量版,由国外开发者在Bitwarden的基础上,采用Rust语言重写而成。 (一)Vaultwarden镜像的作用及特点 轻量级与高性…...
