用环形数组实现队列(多种高级方法,由浅入深)

同普通数组实现的队列相比,普通数组的头结点和尾节点都是固定的,在进行移除的时候如果移除了一个节点,后面所有节点都需要进行移除操作,需要的时间复杂度更高
在环形数组中,确定了头尾指针的环形数组很好地解决了这一点
我们来看具体思路
方法一:牺牲一个存储容量

有两个指针,在环形数组为空的时候它们都指向这个0索引

加入元素之后,尾指针后移一位,直到尾指针的 下一个和头指针重合,如图

在进行移除操作的时候,将头指针前进一位即可

isfull:当尾指针的下一个位置与头指针重合时,说明环形数组已经满了
用索引来表示的话每次让移动让tail+1,和数组长度取模即可,再和head的值进行判断
isempty:当尾指针与头指针重合的时候,说明环形数组为空
为了使下标可以为0到4循环,我们需要控制tail和head,所以我们可以这么表示
进行head和tail的迭代
head=(head+1)%array.length;tail=(tail+1)%array.length;在迭代器中,将初始节点定位为p=head,循环条件为p!=tail,因为tail指的是下一个存入元素的数组位置
我们来看方法实现
public class ArrayQueue1 <E>implements Queue<E>,Iterable<E>{private E[] array;private int head=0;private int tail=0;@SuppressWarnings("all")public ArrayQueue1(int capacity) {array = (E[]) new Object[capacity+1];}@Overridepublic Iterator<E> iterator() {return new Iterator<E>() {int p=head;@Overridepublic boolean hasNext() {return p!=tail;}@Overridepublic E next() {E value=array[p];p=(p+1)%array.length;return value;}};}@Overridepublic boolean offer(E value) {if(isFull()){return false;}array[tail]=value;tail=(tail+1)%array.length;return true;}@Overridepublic E poll() {if(isEmpty()){return null;}E value=array[head];head=(head+1)%array.length;return value;}@Overridepublic E peek() {if(isEmpty()){return null;}return array[head];}@Overridepublic boolean isEmpty() {return head==tail;}@Overridepublic boolean isFull() {return (tail+1)%array.length==head;}
}方法二:通过数组内元素个数进行判断
和之前的思路相近,我们多设置一个size记录元素个数,这个时候不需要牺牲一个存储容量,在isfull判断中直接通过比较size和数组长度,在非空判断中,判断size是否为0即可
关于迭代器遍历,我们需要再引入一个变量count,初始值赋值为0,循环条件是count<size,因为size代表元素个数
我们来看代码
ic class ArrayQueue2 <E>implements Queue<E>,Iterable<E>{private E[] array;private int head=0;private int tail=0;private int size=0;//队列中元素个数@SuppressWarnings("all")public ArrayQueue2(int capacity) {array = (E[]) new Object[capacity];}@Overridepublic Iterator<E> iterator() {return new Iterator<E>() {int p=head;int count=0;@Overridepublic boolean hasNext() {return count<size;}@Overridepublic E next() {E value=array[p];p=(p+1)%array.length;count++;return value;}};}@Overridepublic boolean offer(E value) {if(isFull()){return false;}array[tail]=value;tail=(tail+1)%array.length;size++;return true;}@Overridepublic E poll() {if(isEmpty()){return null;}E value=array[head];head=(head+1)%array.length;size--;return value;}@Overridepublic E peek() {if(isEmpty()){return null;}return array[head];}@Overridepublic boolean isEmpty() {return size==0;}@Overridepublic boolean isFull() {return size==array.length;}
}
方法三:不通过牺牲元素和进行headtail处理

我们还是设置头尾指针,我们以上图为例子,有一个长度为3的环形数组
我们一直将head和tail进行移动的时候递增,不再通过head和tail做处理来代表索引,而是通过将递增的head和tail进行计算来求索引,我们不再通过array[head]或者array[tail]代表元素值,而是通过
array[head%array.length]和array[tail%array.length]
在进行非空判断的时候,思路还是tail=head
在进行非满判断的时候,思路则是通过tail-head等不等于数组长度,无需牺牲一个存储空间。
我们来看代码
public class ArrayQueue3<E> implements Queue<E>, Iterable<E>{private final E[] array;private int head = 0;private int tail = 0;@SuppressWarnings("all")public ArrayQueue3(int capacity) {array = (E[]) new Object[capacity];}@Overridepublic Iterator<E> iterator() {return new Iterator<E>() {int p=head;@Overridepublic boolean hasNext() {return p!=tail;}@Overridepublic E next() {E value=array[head%array.length];p++;return value;}};}@Overridepublic boolean offer(E value) {if(isFull()){return false;}array[tail%array.length] = value;tail++;return true;}@Overridepublic E poll() {if (isEmpty()){return null;}E value=array[head%array.length];head++;return value;}@Overridepublic E peek() {if (isEmpty()){return null;}E vakue=array[head%array.length];return vakue;}@Overridepublic boolean isEmpty() {return head == tail;}@Overridepublic boolean isFull() {return tail-head == array.length;}
}
一些问题思考
在方法三中,我们不对head和tail进行处理,而是放任其递增,因为int是有范围的,再超过tail的最大范围之后会报错,所以我们思考处理方法
第一种方法,通过转成长整型long避免越界报错,强制转型
array[(int) (Integer.toUnsignedLong(tail)%array.length)]但是所有涉及的数组都需要进行强制转型,会比较复杂
二进制中按位与运算
求模运算:
- 如果除数是2的n次方
- 那么被除数的后n位即为余数(模)
- 求被除数的后n位方法:与2^n-1次方进行按位与运算
array[head&(array.length-1)];修改如上
如果数组长度不是2的n次方,我们该如何应对呢
将数组长度根据传入参数设置成2的n次方
第一种方法直接抛出异常
2^n&2^n-1=0
我们可以根据这个规律直接抛出异常
public ArrayQueue3(int capacity) {//1.抛异常if((capacity&capacity-1)!=0){throw new IllegalArgumentException("capacity must be a power of 2");}array = (E[]) new Object[capacity];}第二种方法是修改传入参数
我们先看思路,假设传进来的数值是30

我们需要将30改成32,也就是找到最近的2的n次方等于32,
我们可以看到log2(30)大约是等于4.几,为了使其变成5,我们可以将log(30)+1,并将其强制转型为整型
又因为idea java语言中的Math包里面只有log10,所以我们可以使用换底公式
但是如果说本来这个数字就是2的n次幂的话再+1就会修改它的值,所以我们可以给传入的参数值进行-1处理,这样就可以很好的避免
在我们得到了n次幂的基础上,我们只需要对1进行左移即可(2^0=1)
代码如下
public static void main(String[] args) {int c=30;int n=(int)(Math.log10(c-1)/Math.log10(2))+1;System.out.println(1<<n);}或者我们也可以直接利用一个公式
求离C最近,比C大的2^n次幂
c-=1;
c|=c>>1;
c|=c>>2;
c|=c>>4;
c|=c>>8;
c|=c>>16;
c+=1;
代码如下
@SuppressWarnings("all")public ArrayQueue3(int c) {c-=1;c|=c>>1;c|=c>>2;c|=c>>4;c|=c>>8;c|=c>>16;c+=1;array = (E[]) new Object[c];}相关文章:

用环形数组实现队列(多种高级方法,由浅入深)
同普通数组实现的队列相比,普通数组的头结点和尾节点都是固定的,在进行移除的时候如果移除了一个节点,后面所有节点都需要进行移除操作,需要的时间复杂度更高 在环形数组中,确定了头尾指针的环形数组很好地解决了这一…...

springboot框架使用RabbitMQ举例代码
以前分享过一个理论有兴趣的小伙伴可以看下 https://blog.csdn.net/Drug_/article/details/138164180 不多说 还是直接上代码 第一步:引入依赖 可以不指定版本 <!-- amqp --><dependency><groupId>org.springframework.boot</groupId…...

Java实现一个延时队列
文章目录 前言正文一、基本概念1.1 延时队列的特点1.2 常见的实现方式 二、Java原生的内存型延时队列2.1 定义延时元素DelayedElement2.2 定义延时队列管理器DelayedQueueManager2.3 消费元素2.4 调试2.5 调试结果2.6 精髓之 DelayQueue.poll() 三、基于Redisson的延时队列3.1 …...

为什么说vue是双向数据流
Vue.js 被称为 双向数据绑定(two-way data binding),是因为它支持数据在 视图(View) 和 模型(Model) 之间双向流动。这意味着,当 数据变化 时,视图会自动更新;…...

创造属于你的 Claude Prompt 和个性化 SVG 卡片|对李继刚老师提示词的浅浅解析与总结
❤️ 如果你也关注大模型与 AI 的发展现状,且对大模型应用开发非常感兴趣,我会快速跟你分享最新的感兴趣的 AI 应用和热点信息,也会不定期分享自己的想法和开源实例,欢迎关注我哦! 🥦 微信公众号ÿ…...

redis与本地缓存
本地缓存是将数据存储在应用程序所在的本地内存中的缓存方式。既然,已经有了 Redis 可以实现分布式缓存了,为什么还需要本地缓存呢?接下来,我们一起来看。 为什么需要本地缓存? 尽管已经有 Redis 缓存了,但…...

git撤销commit和add
撤销commit git reset --soft HEAD^撤销add git reset .查看状态 git status...
【361】基于springboot的招生宣传管理系统
摘 要 使用旧方法对招生宣传管理系统的信息进行系统化管理已经不再让人们信赖了,把现在的网络信息技术运用在招生宣传管理系统的管理上面可以解决许多信息管理上面的难题,比如处理数据时间很长,数据存在错误不能及时纠正等问题。这次开发的招…...

【一些关于Python的信息和帮助】
Python是一种广泛使用的高级编程语言,它的设计哲学强调代码的可读性和简洁的语法(尤其是使用空格缩进划分代码块,而不是使用大括号或关键字)。Python支持多种编程范式,包括面向对象、命令式、函数式和过程式编程。 以…...

creo toolkit二次开发学习之程序集(ProAsmcomp)和装配体组件路径对象(ProAsmcomppath)
程序集ProAsmcomp可以理解为装配体组件对象。 对象ProAssembly是ProSolid的一个实例,并共享相同的声明。因此,ProAssembly对象可以作为适用于装配体的任何ProSolid和ProMdl函数的输入。特别是,因为你可以使用函数ProSolidFeatVisit()来遍历特…...

深入浅出 Spring Boot 与 Shiro:构建安全认证与权限管理框架
一、Shiro框架概念 (一)Shiro框架概念 1.概念: Shiro是apache旗下一个开源安全框架,它对软件系统中的安全认证相关功能进行了封装,实现了用户身份认证,权限授权、加密、会话管理等功能,组成一…...

外包干了三年,精神严重内耗...
前段时间我同事(做测试的一个妹子)跟我讲,感觉早上起来十分的疲惫,不想上班,问我们这是什么样的现象,其实有时候我也有这种感觉,虽然我卷,但我也是肉体凡胎啊!不是机器人…...

ruoyi-vue集成tianai-captcha验证码
后端代码 官方使用demo文档:http://doc.captcha.tianai.cloud/#%E4%BD%BF%E7%94%A8demo 我的完整代码:https://gitee.com/Min-Duck/RuoYi-Vue.git 主pom.xml 加入依赖 <!-- 滑块验证码 --><dependency><groupId>cloud.tianai.captc…...

Django安装
在终端创建django项目 1.查看自己的python版本 输入对应自己本机python的版本,列如我的是3.11.8 先再全局安装django依赖包 2.在控制窗口输入安装命令: pip3.11 install django 看到Successflully 说明我们就安装成功了 python的Scripts文件用于存…...

Ubuntu 20.04 安装 QGC v4.3 开发环境
Ubuntu 20.04 安装 QGC开发环境 1. 准备安装 Qt 5.15.2安装依赖获取源码 2. 编译参考 前言 QGC ( QGroundControl) 是一个开源地面站,基于QT开发的,有跨平台的功能。可以在Windows,Android,MacOS或Linux上运行。它可以将PX4固件加…...
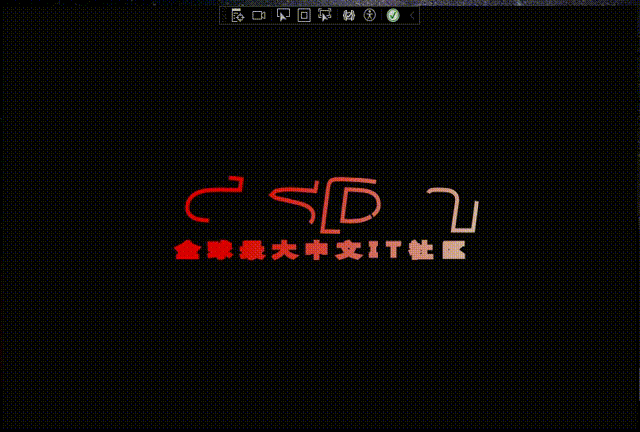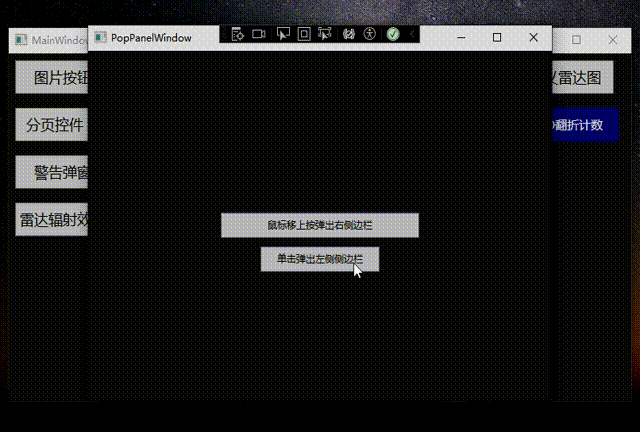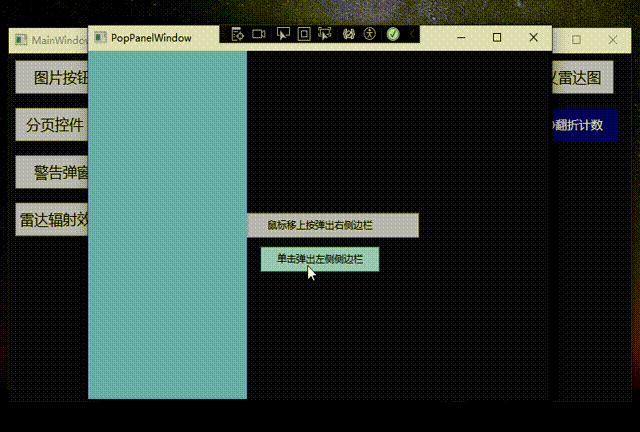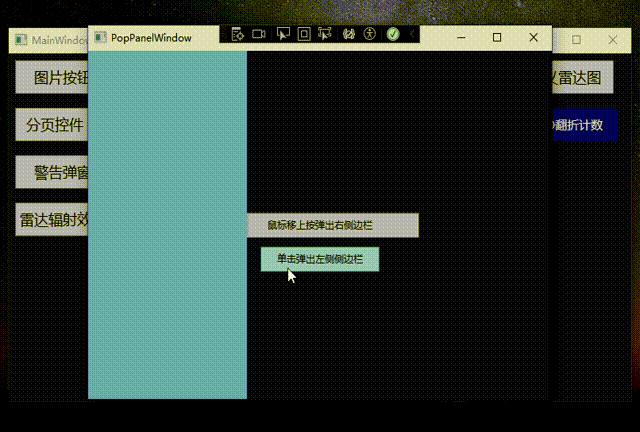
WPF+MVVM案例实战(二十一)- 制作一个侧边弹窗栏(AB类)
文章目录 1、案例效果1、侧边栏分类2、AB类侧边弹窗实现1.文件创建2、样式代码与功能代码实现3、功能代码实现 3 运行效果4、源代码获取 1、案例效果 1、侧边栏分类 A类 :左侧弹出侧边栏B类 :右侧弹出侧边栏C类 :顶部弹出侧边栏D类 …...

linux中怎样登录mysql数据库
在Linux中登录MySQL数据库,可以使用以下命令: mysql -u username -p 其中,username是你的MySQL用户名。运行该命令后,系统会提示你输入密码。 如果MySQL服务器不在本地主机或者你需要指定不同的端口,可以使用以下命…...

深入理解 Linux 内存管理:free 命令详解
在 Linux 系统中,内存是关键的资源之一,管理和监控内存的使用情况对系统的稳定性和性能至关重要。free 命令是 Linux 中用于查看内存使用情况的重要工具,它可以让我们快速了解系统中物理内存和交换分区(Swap)的使用状态…...

指针万字超级最强i解析与总结!!!!!
文章目录 1.内存和地址1.1内存1.2究竟该如何理解编址 2.指针变量和地址2.1 取地址操作符(&)2.2指针变量和解引用操作符(*)2.2.1指针变量2.2.2如何拆解指针类型2.2.3解引用操作符 2.3 指针变量的大小 3.指针变量类型的意义3.1指…...
告别生硬电子音,这款TTS软件让语音转换更自然动听
Balabolka是一款革新性的文本语音转换工具,为用户提供了极其灵活和个性化的阅读体验。这款软件不仅仅是简单的文字朗读器,更是一个智能的语音助手,能够将各类文本瞬间转化为生动自然的语音输出。 软件的核心优势在于其卓越的文件兼容性和多样…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
