MATLAB中eig函数用法
目录
语法
说明
示例
矩阵特征值
矩阵的特征值和特征向量
排序的特征值和特征向量
左特征向量
不可对角化(亏损)矩阵的特征值
广义特征值
病态矩阵使用 QZ 算法得出广义特征值
一个矩阵为奇异矩阵的广义特征值
eig函数的功能是求取矩阵特征值和特征向量。
语法
e = eig(A)
[V,D] = eig(A)
[V,D,W] = eig(A)
e = eig(A,B)
[V,D] = eig(A,B)
[V,D,W] = eig(A,B)
[___] = eig(A,balanceOption)
[___] = eig(A,B,algorithm)
[___] = eig(___,outputForm)说明
e = eig(A) 返回一个列向量,其中包含方阵 A 的特征值。
[V,D] = eig(A) 返回特征值的对角矩阵 D 和矩阵 V,其列是对应的右特征向量,使得 A*V = V*D
[V,D,W] = eig(A) 还返回满矩阵 W,其列是对应的左特征向量,使得 W'*A = D*W'。
特征值问题是用来确定方程 Av = λv 的解,其中,A 是 n×n 矩阵,v 是长度 n 的列向量,λ 是标量。满足方程的 λ 的值即特征值。满足方程的 v 的对应值即右特征向量。左特征向量 w 满足方程 w’A = λw’。
e = eig(A,B) 返回一个列向量,其中包含方阵 A 和 B 的广义特征值。
[V,D] = eig(A,B) 返回广义特征值的对角矩阵 D 和满矩阵 V,其列是对应的右特征向量,使得 A*V = B*V*D。
[V,D,W] = eig(A,B) 还返回满矩阵 W,其列是对应的左特征向量,使得 W'*A = D*W'*B。
广义特征值问题是用来确定方程 Av = λBv 的解,其中,A 和 B 是 n×n 矩阵,v 是长度 n 的列向量,λ 是标量。满足方程的 λ 的值即广义特征值。对应的 v 的值即广义右特征向量。左特征向量 w 满足方程 w’A = λw’B。
[___] = eig(A,balanceOption)(其中,balanceOption 为 'nobalance')禁用该算法中的初始均衡步骤。balanceOption 的默认值是 'balance',表示启用均衡步骤。eig 函数可返回上述语法中的任何输出参数。
[___] = eig(A,B,algorithm)(其中,algorithm 为 'chol')使用 B 的 Cholesky 分解计算广义特征值。algorithm 的默认值取决于 A 和 B 的属性,但通常是 'qz',表示使用 QZ 算法。
如果 A 为埃尔米特并且 B 为埃尔米特正定矩阵,则 algorithm 的默认值为 'chol'。
[___] = eig(___,outputForm) 支持上述语法中的任何输入或输出参数,并以 outputForm 指定的形式返回特征值。将 outputForm 指定为 'vector' 可返回列向量中的特征值,指定为 'matrix' 可返回对角矩阵中的特征值。
示例
矩阵特征值
使用 gallery 创建一个对称正定矩阵。
A = gallery('lehmer',4)
A = 4×41.0000 0.5000 0.3333 0.25000.5000 1.0000 0.6667 0.50000.3333 0.6667 1.0000 0.75000.2500 0.5000 0.7500 1.0000计算 A 的特征值。结果为一个列向量。
e = eig(A)
e = 4×10.20780.40780.84822.5362或者,使用 outputForm 返回对角矩阵中的特征值。
D = eig(A,'matrix')
D = 4×40.2078 0 0 00 0.4078 0 00 0 0.8482 00 0 0 2.5362矩阵的特征值和特征向量
使用 gallery 创建循环矩阵。
A = gallery('circul',3)
A = 3×31 2 33 1 22 3 1
计算 A 的特征值和右特征向量。
[V,D] = eig(A)
V = 3×3 complex-0.5774 + 0.0000i 0.5774 + 0.0000i 0.5774 + 0.0000i-0.5774 + 0.0000i -0.2887 - 0.5000i -0.2887 + 0.5000i-0.5774 + 0.0000i -0.2887 + 0.5000i -0.2887 - 0.5000iD = 3×3 complex6.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i0.0000 + 0.0000i -1.5000 + 0.8660i 0.0000 + 0.0000i0.0000 + 0.0000i 0.0000 + 0.0000i -1.5000 - 0.8660i验证结果是否满足 A*V = V*D。
A*V - V*D
ans = 3×3 complex
10-14 ×-0.2220 + 0.0000i -0.0888 - 0.0111i -0.0888 + 0.0111i0.0888 + 0.0000i 0.0000 + 0.0833i 0.0000 - 0.0833i-0.0444 + 0.0000i -0.1110 + 0.0666i -0.1110 - 0.0666i在理想情况下,特征值分解可满足此关系。由于 eig 使用浮点计算执行分解,那么 A*V 可最大程度接近 V*D。换言之,A*V - V*D 接近但不等于 0。
排序的特征值和特征向量
默认情况下,eig 并不总是返回已排序的特征值和特征向量。可以使用 sort 函数将特征值按升序排序,并重新排序相应的特征向量。
计算 5×5 幻方矩阵的特征值和特征向量。
A = magic(5)
A = 5×517 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9[V,D] = eig(A)
V = 5×5-0.4472 0.0976 -0.6330 0.6780 -0.2619-0.4472 0.3525 0.5895 0.3223 -0.1732-0.4472 0.5501 -0.3915 -0.5501 0.3915-0.4472 -0.3223 0.1732 -0.3525 -0.5895-0.4472 -0.6780 0.2619 -0.0976 0.6330D = 5×565.0000 0 0 0 00 -21.2768 0 0 00 0 -13.1263 0 00 0 0 21.2768 00 0 0 0 13.1263
A 的特征值位于 D 的对角线上。但是,特征值并未排序。
使用 diag(D) 从 D 的对角线上提取特征值,然后按升序对得到的向量进行排序。sort 的第二个输出返回索引的置换向量。
[d,ind] = sort(diag(D))
d = 5×1-21.2768-13.126313.126321.276865.0000ind = 5×123541
使用 ind 对 D 的对角线元素进行重新排序。由于 D 中的特征值对应于 V 的各列中的特征向量,因此还必须使用相同的索引对 V 的列进行重新排序。
Ds = D(ind,ind)
Ds = 5×5-21.2768 0 0 0 00 -13.1263 0 0 00 0 13.1263 0 00 0 0 21.2768 00 0 0 0 65.0000Vs = V(:,ind)
Vs = 5×50.0976 -0.6330 -0.2619 0.6780 -0.44720.3525 0.5895 -0.1732 0.3223 -0.44720.5501 -0.3915 0.3915 -0.5501 -0.4472-0.3223 0.1732 -0.5895 -0.3525 -0.4472-0.6780 0.2619 0.6330 -0.0976 -0.4472(V,D) 和 (Vs,Ds) 都会生成 A 的特征值分解。A*V-V*D 和 A*Vs-Vs*Ds 的结果一致(基于舍入误差)。
e1 = norm(A*V-V*D);
e2 = norm(A*Vs-Vs*Ds);
e = abs(e1 - e2)
e = 1.2622e-29左特征向量
创建一个 3×3 矩阵。
A = [1 7 3; 2 9 12; 5 22 7];计算右特征向量 V、特征值 D 和左特征向量 W。
[V,D,W] = eig(A)
V = 3×3-0.2610 -0.9734 0.1891-0.5870 0.2281 -0.5816-0.7663 -0.0198 0.7912D = 3×325.5548 0 00 -0.5789 00 0 -7.9759W = 3×3-0.1791 -0.9587 -0.1881-0.8127 0.0649 -0.7477-0.5545 0.2768 0.6368验证结果是否满足 W'*A = D*W'。
W'*A - D*W'
ans = 3×3
10-13 ×-0.0444 -0.1066 -0.0888-0.0011 0.0442 0.03330 0.0266 0.0178在理想情况下,特征值分解可满足此关系。由于 eig 使用浮点计算执行分解,那么 W'*A 可最大程度接近 D*W'。换言之,W'*A - D*W' 接近但不等于 0。
不可对角化(亏损)矩阵的特征值
创建一个 3×3 矩阵。
A = [3 1 0; 0 3 1; 0 0 3];计算 A 的特征值和右特征向量。
[V,D] = eig(A)
V = 3×31.0000 -1.0000 1.00000 0.0000 -0.00000 0 0.0000D = 3×33 0 00 3 00 0 3A 包含重复特征值,且特征向量非独立。这意味着 A 不可对角化,因此为亏损矩阵。
尽管 A 为亏损矩阵,仍验证 V 和 D 是否满足方程 A*V = V*D。
A*V - V*D
ans = 3×3
10-15 ×0 0.8882 -0.88820 0 0.00000 0 0在理想情况下,特征值分解可满足此关系。由于 eig 使用浮点计算执行分解,那么 A*V 可最大程度接近 V*D。换言之,A*V - V*D 接近但不等于 0。
广义特征值
创建两个矩阵(A 和 B),然后求解对组 (A,B) 的特征值和右特征向量的广义特征值问题。
A = [1/sqrt(2) 0; 0 1];
B = [0 1; -1/sqrt(2) 0];
[V,D]=eig(A,B)
V = 2×2 complex1.0000 + 0.0000i 1.0000 + 0.0000i0.0000 - 0.7071i 0.0000 + 0.7071iD = 2×2 complex0.0000 + 1.0000i 0.0000 + 0.0000i0.0000 + 0.0000i 0.0000 - 1.0000i验证结果是否满足 A*V = B*V*D。
A*V - B*V*D
ans = 2×20 00 0
残差 A*V - B*V*D 精确为零。
病态矩阵使用 QZ 算法得出广义特征值
创建病态对称矩阵,其包含的值接近计算机精度。
format long e
A = diag([10^-16, 10^-15])
A = 2×21.000000000000000e-16 00 1.000000000000000e-15使用默认算法计算广义特征值和一组右特征向量。在这种情况下,默认算法为 'chol'。
[V1,D1] = eig(A,A)
V1 = 2×21.000000000000000e+08 00 3.162277660168380e+07D1 = 2×29.999999999999999e-01 00 1.000000000000000e+00
现在,使用 'qz' 算法计算广义特征值和一组右特征向量。
[V2,D2] = eig(A,A,'qz')
V2 = 2×21 00 1D2 = 2×21 00 1检查 'chol' 结果满足 A*V1 = A*V1*D1 的程度。
format short
A*V1 - A*V1*D1
ans = 2×2
10-23 ×0.1654 00 -0.6617
现在,检查 'qz' 结果满足 A*V2 = A*V2*D2 的程度。
A*V2 - A*V2*D2
ans = 2×20 00 0
当两个矩阵均为对称矩阵时,eig 默认使用 'chol' 算法。在这种情况下,QZ 算法可返回更精确的结果。
一个矩阵为奇异矩阵的广义特征值
创建一个 2×2 单位矩阵 A 和一个奇异矩阵 B。
A = eye(2);
B = [3 6; 4 8];如果尝试用命令 [V,D] = eig(B\A) 计算矩阵 B^−1A 的广义特征值,则 MATLAB® 会返回错误,因为 B\A 会生成 Inf 值。
在这种情况下,应将上述两个矩阵传递给 eig 函数,计算广义特征值和右特征向量。
[V,D] = eig(A,B)
V = 2×2-0.7500 -1.0000-1.0000 0.5000D = 2×20.0909 00 Inf
最好是分开传递两个矩阵,并让 eig 选择求解该问题的最佳算法。在这种情况下,eig(A,B) 会返回一组特征向量和至少一个实数特征值,尽管 B 不可逆。
验证第一个特征值和第一个特征向量是否满足 ![]()
eigval = D(1,1);
eigvec = V(:,1);
A*eigvec - eigval*B*eigvec
ans = 2×1
10-15 ×0.11100.2220
在理想情况下,特征值分解可满足此关系。由于分解是使用浮点计算完成的,那么 A*eigvec 可最大程度接近 eigval*B*eigvec,本例中确实如此。
提示
-
eig 函数可以计算实数对称稀疏矩阵的特征值。要计算稀疏矩阵的特征向量或计算非实数对称稀疏矩阵的特征值,请使用 eigs 函数。
相关文章:

MATLAB中eig函数用法
目录 语法 说明 示例 矩阵特征值 矩阵的特征值和特征向量 排序的特征值和特征向量 左特征向量 不可对角化(亏损)矩阵的特征值 广义特征值 病态矩阵使用 QZ 算法得出广义特征值 一个矩阵为奇异矩阵的广义特征值 eig函数的功能是求取矩阵特征值…...

Chrome(谷歌浏览器中文版)下载安装(Windows 11)
目录 Chrome_10_30工具下载安装 Chrome_10_30 工具 系统:Windows 11 下载 官网:https://chrome.google-zh.com/,点击立即下载 下载完成(已经下过一遍所以点了取消) 安装 解压,打开安装包 点击下一步…...

Linux 配置JDK
文章目录 一、下载Oracle-JDK1.1、如何正确的下载JDK 二、配置JDK环境变量2.1 环境变量配置2.1.1、修改vim /etc/profile 添加jdk的路径 一、下载Oracle-JDK 1.1、如何正确的下载JDK 首先我要安装的是oracle-jdk,这个时候什么地方都不要去,就去oracle的…...

目前主流的人工智能学习框架有哪些?
随着人工智能(AI)技术的蓬勃发展,越来越多的AI学习框架相继推出,成为开发者、研究人员和企业构建机器学习(ML)和深度学习(DL)模型的首选工具。AI学习框架不仅提供了丰富的工具库和函…...

100种算法【Python版】第57篇——贝叶斯优化算法
本文目录 1 算法说明2 贝叶斯优化的步骤3 算法应用1:目标函数最大值4 算法应用2:确定最佳试验参数1 算法说明 贝叶斯优化是一种旨在优化黑箱目标函数的策略,通常适用于评估代价高昂或时间消耗长的函数。它利用贝叶斯统计方法来构建目标函数的概率模型,进而指导下一步的采样…...

在Ubuntu 上实现 JAR 包的自启动
在 Ubuntu 上实现 JAR 包的自启动,可以通过以下几种方法: 方法一:使用 systemd 创建一个服务文件: 在 /etc/systemd/system/ 目录下创建一个新的服务文件,例如 myapp.service: sudo nano /etc/systemd/sys…...

【智能算法应用】哈里斯鹰算法优化二维栅格路径规划问题
摘要 本文研究了基于哈里斯鹰优化算法(Harris Hawks Optimization, HHO)的二维栅格路径规划方法。HHO算法模拟哈里斯鹰的猎食行为,通过迭代搜索过程找到从起点到终点的最优路径,避开栅格中的障碍物。实验结果表明,HHO…...

单品年销10亿!看麻辣王子是如何布局软文营销为品牌赋能的?
说到辣条,除了大家熟知的卫龙之外,还有一个不得不提的品牌就是——麻辣王子。 作为来自辣条发源地湖南平江的老牌辣条企业,麻辣王子近几年通过打造品牌,积极破圈,2023年凭借一款单品狂揽超10亿年销售额,稳…...

【开源免费】基于SpringBoot+Vue.JS医院管理系统(JAVA毕业设计)
博主说明:本文项目编号 T 062 ,文末自助获取源码 \color{red}{T062,文末自助获取源码} T062,文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析…...

C++:模拟实现STL的string
目录 一.实现string类 1.string的构造及析构 2.string类的遍历 3.string类的插入和删除 4.string类的空间处理 5.string类的查找 6.string类的输出和输入 7.string类的常用判断 二.整体代码 1.string.h 2.string.cpp 一.实现string类 在前一节中我们了解了STL中stri…...

【Python TensorFlow】入门到精通
TensorFlow 是一个开源的机器学习框架,由 Google 开发,广泛应用于机器学习和深度学习领域。本篇将详细介绍 TensorFlow 的基础知识,并通过一系列示例来帮助读者从入门到精通 TensorFlow 的使用。 1. TensorFlow 简介 1.1 什么是 TensorFlow…...

数据结构:七种排序及总结
文章目录 排序一插入排序1直接插入排序2希尔排序二选择排序3直接选择排序4堆排序三 交换排序5冒泡排序6快速排序四 归并排序7归并排序源码 排序 我们数据结构常见的排序有四大种,四大种又分为七小种,如图所示 排序:所谓排序,就是…...
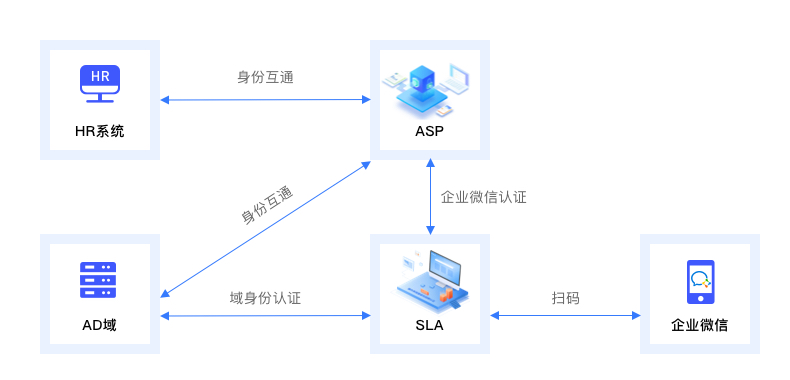
【安当产品应用案例100集】030-使用企业微信登录Windows,实现工作电脑与业务系统登录方式统一
随着越来越多的企业信息系统从intranet开放到internet,企业员工的办公接入方式也越发多样,信息系统面临的数据安全问题也呈现爆发的趋势。一些大企业,比如Google、Microsoft、Huawei有强大的开发能力、IT能力,可以构建出自己的零信…...

大数据数据存储层MemSQL, HBase与HDFS
以下是对 MemSQL、HBase 和 HDFS 的详细介绍,这些工具在分布式数据存储和处理领域有着重要作用。 1. MemSQL MemSQL(现称为 SingleStore)是一种分布式内存数据库,兼具事务处理(OLTP)和分析处理(OLAP)的能力,专为高性能实时数据处理设计。 1.1 核心特点 内存优先存储…...

【HarmonyOS】鸿蒙应用设置控件通用样式AttributeModifier, @Styles
【HarmonyOS】鸿蒙应用设置控件通用样式AttributeModifier, Styles 前言 在鸿蒙中UI开发经常需要对控件样式进行统一的封装,在API早前版本,一般是通过 Styles进行样式封装复用: Entry Component struct Index {build() {Column(…...

Scala IF...ELSE 语句
Scala IF...ELSE 语句 Scala 是一种多范式的编程语言,它结合了面向对象和函数式编程的特点。在 Scala 中,if...else 语句是一种基本且常用的控制结构,用于根据条件执行不同的代码块。与 Java 或 Python 等其他语言中的 if...else 语句类似&a…...
快速上手vue3+js+Node.js
安装Navicat Premium Navicat Premium 创建一个空的文件夹(用于配置node) 生成pakeage.json文件 npm init -y 操作mysql npm i mysql2.18.1 安装express搭建web服务器 npm i express4.17.1安装cors解决跨域问题 npm i cors2.8.5创建app.js con…...

06 网络编程基础
目录 1.通信三要素 1. IP地址(Internet Protocol Address) 2. 端口号(Port Number) 3. 协议(Protocol) 2.TCP与UDP协议 三次握手(Three-Way Handshake) 四次挥手(…...
)
Python 的 FastApi 如何在request 重复取request.body()
需求背景: 需要再中间件中获取body 中的信息 但是 又想要在之后 还可以重复取 这个body 因为有的接口写法是直接从body中获取参数,然而这个body是数据流的形式,一旦取一次就导致后面取不到里面的值了 。 解决方式: 1.保存请求体: 在中间件中读取请求…...

qt QFontDialog详解
1、概述 QFontDialog 是 Qt 框架中的一个对话框类,用于选择字体。它提供了一个可视化的界面,允许用户选择所需的字体以及相关的属性,如字体样式、大小、粗细等。用户可以通过对话框中的选项进行选择,并实时预览所选字体的效果。Q…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...
