LeetCode 0685.冗余连接 II:并查集(和I有何不同分析)——详细题解(附图)
【LetMeFly】685.冗余连接 II:并查集(和I有何不同分析)——详细题解(附图)
力扣题目链接:https://leetcode.cn/problems/redundant-connection-ii/
在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
示例 1:
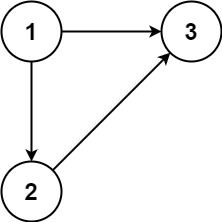
输入:edges = [[1,2],[1,3],[2,3]] 输出:[2,3]
示例 2:
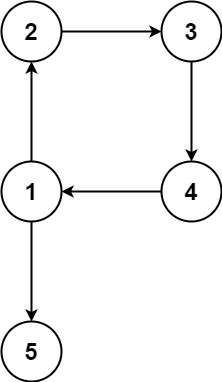
输入:edges = [[1,2],[2,3],[3,4],[4,1],[1,5]] 输出:[4,1]
提示:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ui, vi <= n
解题方法:并查集

解题思路
这题和684.冗余连接的区别是:
684的无向图只需要考虑有没有形成自环,而本题有向图还需要考虑“是否形成了入度为2的节点”。
如果形成了“入度为2”的节点,例如下面两种情况,在684.冗余连接中只需要移除“首次形成(无向)环”的边,而在685.冗余连接II中就不能只移除“最后出现的导致形成(无向)环的边”:
1----->2 1------+ ↑ ↑ ↑ ↓ 3------+ 2<-----3<---4左图中只能移除
[1,2]或[3,2]而不能移除[3,1];右图中只能移除[1,3]而不能移除[3,2]或[2,1]。
有向边不能和无向边一概而论的本质原因是:树中一个节点不能有两个父节点,即入度不能为2。所以,一旦出现了入度为2的节点 n o d e node node,就要在“终点为 n o d e node node的两条边”里面选择一条移除。判断方法如下:
尝试移除一条边,判断剩下的边(不考虑方向)能否构成无向环,如果不构成无向环则说明这条边可以被移除。
判断方法就和
684题一模一样了,使用并查集即可完成判断。
树上多一条边就一定存在入度为2的节点吗?不一定,还可能有以下这种情况:
1------+ ↑ ↓ 2<-----3----->4图中节点
[1,2,3]形成了一个环,但1、2、3、44个节点的入度都为1。这样就和
684题一模一样了其实,在环[1,2,3]里任意移除一条边图都能变成树。同样使用并查集,返回第一条“形成环”的边即为所求。
解题方法
首先统计是否有入度为2的节点:
- 若有,则尝试移除指向
2的边(若移除后图中无环则这条边可以被移除) - 否则,移除第一条导致“环出现”的边
常见问题回答Q&A
Q1: 若有入度为2的节点,在判断“移除一条边后图是否为树”时,能否通过“统计每个点是否孤立(入度出度都为0)”来判断?
例如下图中终点为3的边有[1,3]和[4,3]两条,移除[4,3]的话会导致点4成为孤立点,因此只能移除[1,3]。
1------+
↑ ↓
2<-----3<---4
A1: 不能这么判断。例如下图只能移除[2,4]不能移除[5,2],但其实移除其中的任意一条都不会产生“孤立点”。
+---+
↓ ↑
4-->2↑
1-->5-->3
建议修改为“通过判断图是否联通”的方式判断某条边是否可以移除。
时空复杂度
- 时间复杂度最坏 O ( n log n ) O(n\log n) O(nlogn),平均为 O ( n α ( n ) ) O(n\alpha(n)) O(nα(n))(接近 O ( n ) O(n) O(n))
- 空间复杂度 O ( n ) O(n) O(n)
AC代码
C++
class Solution {
private:vector<int> fa;bool couldRemoveThisEdge(vector<vector<int>>& edges, int index) {initFa(edges.size());for (int i = 0; i < edges.size(); i++) {if (i == index) {continue;}if (find(edges[i][0]) == find(edges[i][1])) {return false;}union_(edges[i][0], edges[i][1]);}return true;}vector<int> solution_indegree(vector<vector<int>>& edges, int node) {for (int i = edges.size() - 1; i >= 0; i--) {if (edges[i][1] == node && couldRemoveThisEdge(edges, i)) {return edges[i];}}return {}; // FAKE RETURN}int find(int x) {if (x != fa[x]) {fa[x] = find(fa[x]);}return fa[x];}void union_(int x, int y) {fa[find(x)] = find(y);}void initFa(int n) {fa.resize(n + 1);for (int i = 1; i <= n; i++) {fa[i] = i;}}vector<int> solution_unionFind(vector<vector<int>>& edges) {initFa(edges.size());for (vector<int>& edge : edges) {if (find(edge[0]) == find(edge[1])) {return edge;} else {union_(edge[0], edge[1]);}}return {}; // FAKE RETURN}
public:vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {vector<bool> inDegree(edges.size() + 1);for (vector<int>& edge : edges) {if (inDegree[edge[1]]) { // 找到了入度为2的点return solution_indegree(edges, edge[1]);} else {inDegree[edge[1]] = true;}}return solution_unionFind(edges);}
};
Python
from typing import Listclass Solution:def initFa(self) -> None:for i in range(1, len(self.edges) + 1):self.fa[i] = idef find(self, x: int) -> int:if self.fa[x] != x:self.fa[x] = self.find(self.fa[x])return self.fa[x]def union(self, x: int, y: int) -> None:self.fa[self.find(x)] = self.find(y)def couldRemoveThisEdge(self, index: int) -> bool:self.initFa()for i in range(len(self.edges)):if i == index:continueif self.find(self.edges[i][0]) == self.find(self.edges[i][1]):return Falseelse:self.union(self.edges[i][0], self.edges[i][1])return Truedef solution_indegree(self, node: int) -> List[int]:for i in range(len(self.edges) - 1, -1, -1):if self.edges[i][1] == node and self.couldRemoveThisEdge(i):return self.edges[i]return [] # FAKE RETURNdef solution_unionFind(self) -> List[int]:self.initFa()for x, y in self.edges:if self.find(x) == self.find(y):return [x, y]else:self.union(x, y)return [] # FAKE RETURNdef findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:self.fa = [0] * (len(edges) + 1)self.edges = edgeshasIndegree = [False] * (len(edges) + 1)for x, y in edges:if hasIndegree[y]:return self.solution_indegree(y)else:hasIndegree[y] = Truereturn self.solution_unionFind()
Java
class UnionFind {private int[] fa;public UnionFind(int n) {fa = new int[n + 1];for (int i = 1; i <= n; i++) {fa[i] = i;}}private int find(int x) {if (fa[x] != x) {fa[x] = find(fa[x]);}return fa[x];}public boolean isUnion(int x, int y) {return find(x) == find(y);}public void union(int x, int y) {fa[find(x)] = find(y);}
}class Solution {private boolean canRemoveThisEdge(int[][] edges, int index) {UnionFind unionFind = new UnionFind(edges.length);for (int i = 0; i < edges.length; i++) {if (i == index) {continue;}if (unionFind.isUnion(edges[i][0], edges[i][1])) {return false;} else {unionFind.union(edges[i][0], edges[i][1]);}}return true;}private int[] solution_indegree(int[][] edges, int node) {for (int i = edges.length - 1; i >= 0; i--) {if (edges[i][1] == node && canRemoveThisEdge(edges, i)) {return edges[i];}}return new int[0]; // FAKE RETURN}private int[] solution_unionFind(int[][] edges) {UnionFind unionFind = new UnionFind(edges.length);for (int[] edge : edges) {if (unionFind.isUnion(edge[0], edge[1])) {return edge;} else {unionFind.union(edge[0], edge[1]);}}return new int[0]; // FAKE RETURN}public int[] findRedundantDirectedConnection(int[][] edges) {boolean[] hasIndegree = new boolean[edges.length + 1];for (int[] edge : edges) {if (hasIndegree[edge[1]]) {return solution_indegree(edges, edge[1]);} else {hasIndegree[edge[1]] = true;}}return solution_unionFind(edges);}
}
Go
package maintype UnionFind struct {fa []int
}func New(n int) UnionFind {fa := make([]int, n + 1)for th, _ := range fa {fa[th] = th}return UnionFind{fa}
}func (unionFind UnionFind) _find(x int) int {if unionFind.fa[x] != x {unionFind.fa[x] = unionFind._find(unionFind.fa[x])}return unionFind.fa[x]
}func (unionFind UnionFind) isUnion(x, y int) bool {return unionFind._find(x) == unionFind._find(y)
}func (unionFind UnionFind) union(x, y int) {unionFind.fa[unionFind._find(x)] = unionFind._find(y)
}func canRemoveThisEdge(edges [][]int, index int) bool {unionFind := New(len(edges))for i := 0; i < len(edges); i++ {if i == index {continue}if unionFind.isUnion(edges[i][0], edges[i][1]) {return false} else {unionFind.union(edges[i][0], edges[i][1])}}return true
}func solution_indegree(edges [][]int, node int) []int {for i := len(edges) - 1; i >= 0; i-- {if edges[i][1] == node && canRemoveThisEdge(edges, i) {return edges[i]}}return make([]int, 0) // FAKE RETURN
}func solution_unionFind(edges [][]int) []int {unionFind := New(len(edges))for _, edge := range edges {if unionFind.isUnion(edge[0], edge[1]) {return edge} else {unionFind.union(edge[0], edge[1])}}return make([]int, 0) // FAKE RETURN
}func findRedundantDirectedConnection(edges [][]int) []int {hasIndegree := make([]bool, len(edges) + 1)for _, edge := range edges {if hasIndegree[edge[1]] {return solution_indegree(edges, edge[1])} else {hasIndegree[edge[1]] = true}}return solution_unionFind(edges)
}
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/143470538
相关文章:

LeetCode 0685.冗余连接 II:并查集(和I有何不同分析)——详细题解(附图)
【LetMeFly】685.冗余连接 II:并查集(和I有何不同分析)——详细题解(附图) 力扣题目链接:https://leetcode.cn/problems/redundant-connection-ii/ 在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点&…...

Dubbo负载均衡
负载均衡策略与配置细节 Dubbo 内置了 client-based 负载均衡机制,如下是当前支持的负载均衡算法,结合上文提到的自动服务发现机制,消费端会自动使用 Weighted Random LoadBalance 加权随机负载均衡策略 选址调用。 如果要调整负载均衡算法…...

PymuPDF4llm提取pdf文件文字、表格与图片
一、PymuPDF4llm 的功能特点 (一)文本提取 简单易用 PymuPDF4llm 的文本提取功能非常简单易用。只需使用pip install pymupdf4llm进行安装,然后通过import pymupdf4llm导入库,就可以使用md_text pymupdf4llm.to_markdown("…...

20241108通过iperf3确认中科创达的高通CM6125的WIFI的网速【失败】
20241108通过iperf3确认中科创达的高通CM6125的WIFI的网速【失败】 2024/11/8 15:43 由于以太网不能用,那就测试一下WIFI,iperf3链接/测试异常。 一般认为可能的原因有: 1、CM6125开发板的WIFI不带天线,影响性能。 2、CM6125的And…...

Stored procedures in PostgreSQL
select 存储过程,在现了解的情况,还是没有mysql,sqlserver等好写好用。 --postgreSQL 11.0 以下版本 create or replace FUNCTION procInsertSchool (pSchoolId Char(5),pSchoolName VarChar(100),pSchoolTelNo VarChar(8) ) RETURNS void language plp…...

第10章 多表查询
一、什么是多表查询 多表查询,也称为关联查询,指两个或更多个表一起完成查询操作。 前提条件:这些一起查询的表之间是有关系的(一对一、一对多),它们之间一定是有关联字段,这个关联字段可能建立…...

【基于LSM的ELF文件安全模块设计】参考
《基于LSM的ELF文件安全模块设计文档》 一、设计目标 本设计致力于通过 Linux 安全模块(LSM)构建一个强大而严密的安全防护体系,以实现对 ELF 文件(涵盖可执行文件和动态链接库)的绝对严格的合法性和完整性检查。其核…...

全卷积和全连接
全连接网络和全卷积网络不一样 以下是对两者的正确解释和代码示例: 1. 全连接网络(Fully Connected Network) 全连接网络使用的是 线性层(nn.Linear),也就是我们常说的“全连接层”。它是用于将每一个输入…...

Unity图形学之Shader结构
Unity - Manual: ShaderLab: Legacy Lighting 1.Shader 语言: OpenGL:SGL 跨平台性能非常好 GLSL语言 OpenGL Shader LanguageDX:微软 非跨平台 性能非常好 HLSL语言 High Level Shader LanguageCG:微软和英伟达 联合开发CG …...

离散时间信号的产生
文章目录 前言1.单位冲激序列函数1.2 函数:1.3 实现代码:1.3 调用方式1.4 调用结果 2.单位阶跃序列函数2.1 函数2.2实现代码2.3调用方式2.4调用结果 3.矩形序列3.1函数3.2 实现代码3.3调用方式3.4 调用结果 4.实指数序列4.1函数4.2实现代码4.3调用方式4.…...
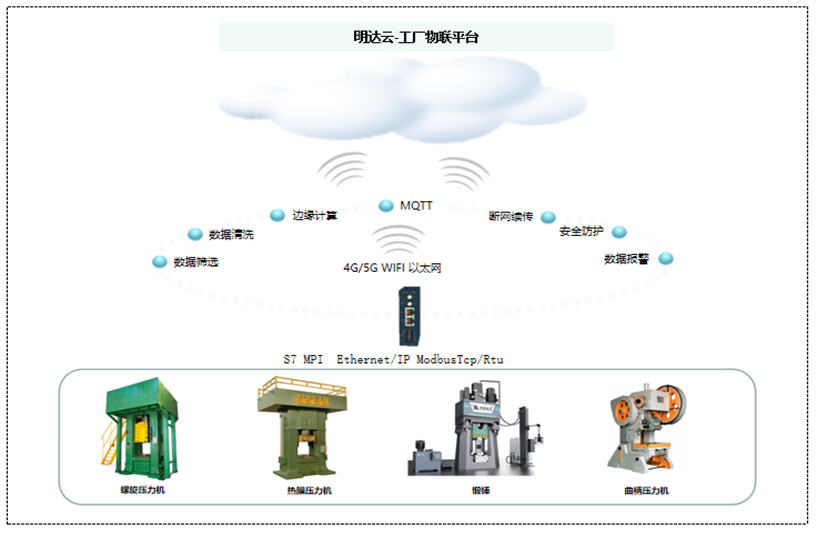
物联优化汽车齿轮锻造
在汽车齿轮的锻造工艺中,锻造温度、锻造压力与行程、锻造速度与锤击方式以及热处理工艺等核心参数扮演着举足轻重的角色。这些参数的精准控制与实时监测,对于提升生产效率、确保产品质量、削减生产成本以及推动生产智能化转型具有不可估量的价值。明达技…...

CocosCreator 构建透明背景应用(最新版!!!)
文章目录 透明原理补充设置截图以及代码step1: electron-js mian.jsstep2:ENABLE_TRANSPARENT_CANVASstep3:SOLID_COLOR Transparentstep:4 Build Web phonestep5:package electron-js & change body background-color 效果图补充 透明原理 使用Cocos creator 做桌面应用开…...

使用CentOS宝塔面板docker搭建EasyTier内网穿透服务
0. 前言 EasyTier是一个简单、安全、去中心化的内网穿透 VPN 组网方案,部署方便,支持 MacOS/Linux/Windows/FreeBSD/Android平台,而且作者搭建了一个公共服务器,不想折腾自建服务,可以使用默认的公共服务器地址 tcp:/…...

HTMLCSS: 实现可爱的冰墩墩
效果演示 HTML <div class"wrap"><div class"body"></div><div class"ear"></div><div class"ear rightEar"></div><div class"leftHand"></div><div class"…...

天地图入门|标注|移动飞行|缩放,商用地图替换
“天地图”是国家测绘地理信息局建设的地理信息综合服务网站。集成了来自国家、省、市(县)各级测绘地理信息部门,以及相关政府部门、企事业单位 、社会团体、公众的地理信息公共服务资源,如果做的项目是政府部门、企事业单位尽量选…...

Flutter PC端UI组件库
一、参考Element-ui的设计和交互,构建基于dart的Flutter UI组件库 https://javonhuang.github.io/sky-ui-page/index.html...

NVR小程序接入平台/设备EasyNVR多品牌NVR管理工具/设备汇聚公共资源场景方案全析
随着信息技术的飞速发展,视频监控已经成为现代社会安全管理和业务运营不可或缺的一部分。特别是在公共资源管理方面,视频监控的应用日益广泛,涵盖了智慧城市、智能交通、大型企业以及校园安防等多个领域。NVR小程序接入平台EasyNVR作为一款功…...
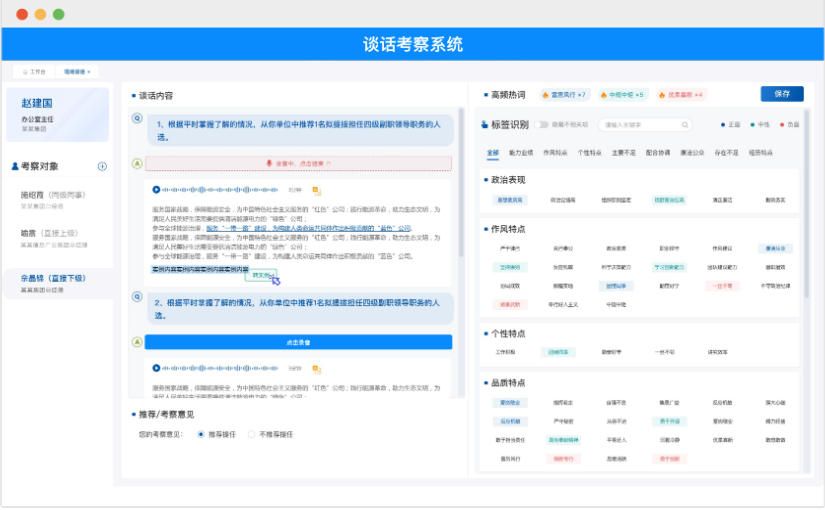
干部谈话考察系统:革新传统,精准高效
在干部选拔任用和考核评价的过程中,谈话考察一直是关键环节之一。然而,传统的谈话考察方式却面临着诸多痛点,严重影响了干部考察工作的质量和效率。干部谈话考察系统的出现,为解决这些问题提供了有力的武器。 一、传统谈话考察的…...
)
反转链表(Leetcode)
反转链表 Leetcode题目链接 题意:翻转一个单链表 🌰: 输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL 在链表本身进行反转即可,不用重新定义链表,这同时浪费时间和空间。 需要采用哑…...

制作游戏外挂的技术栈有哪些
制作游戏外挂是一项涉及多方面技术的复杂任务。这项技术通常被用于在游戏中获得不公平的优势,因此也遭到了大量的讨论与争议。制作外挂需要深厚的编程基础、对系统底层的深入理解以及对具体游戏架构的详细研究。以下是一篇全面的分析文章,旨在揭示制作游…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
