离散时间信号的产生
文章目录
- 前言
- 1.单位冲激序列函数
- 1.2 函数:
- 1.3 实现代码:
- 1.3 调用方式
- 1.4 调用结果
- 2.单位阶跃序列函数
- 2.1 函数
- 2.2实现代码
- 2.3调用方式
- 2.4调用结果
- 3.矩形序列
- 3.1函数
- 3.2 实现代码
- 3.3调用方式
- 3.4 调用结果
- 4.实指数序列
- 4.1函数
- 4.2实现代码
- 4.3调用方式
- 4.4调用结果
- 5.正弦型序列
- 5.1函数
- 5.2实现代码
- 5.3调用方式
- 5.4调用结果
- 6.复指数序列
- 6.1函数
- 6.2实现代码
- 6.3调用方式
- 6.4调用结果
- 备注
- 7.序列的简单运算
- 7.1序列相加
- 7.1.1 代码实现
- 7.1.2 调用测试
- 7.1.3 调用结果
- 7.2序列相乘
- 7.2.1 代码实现
- 7.2.2 调用测试
- 7.2.3 调用结果
- 7.3序列移位
- 7.3.1 代码实现
- 7.3.2 调用测试
- 7.3.3 调用结果
- 7.4 序列翻褶
- 7.4.1 代码实现
- 7.4.2 调用测试
- 7.4.3 调用结果
- 结语
前言
本篇博客介绍了基于matlab的数字信号处理中的常见离散时间信号,以及常见的序列运算,并通过编写代码实现相关运算。
1.单位冲激序列函数
1.2 函数:

1.3 实现代码:
function [x,n] = impseq(n0,n1,n2)% Generates x(n) = delta(n-n0); n1 <= n,n0 <= n2% ----------------------------------------------% [x,n] = impseq(n0,n1,n2)%if ((n0 < n1) || (n0 > n2) || (n1 > n2))error('arguments must satisfy n1 <= n0 <= n2')endn = n1:n2;%x = [zeros(1,(n0-n1)), 1, zeros(1,(n2-n0))];x = (n-n0) == 0;1.3 调用方式
[x,n]=impseq(1,-2,5);
% n=[-2,-1,0,1,2,3,4,5]
% x= 1x8 logical
stem(n,x,"filled")
1.4 调用结果

2.单位阶跃序列函数
2.1 函数

2.2实现代码
function [x,n] = stepseq(n0,n1,n2)% Generates x(n) = u(n-n0); n1 <= n,n0 <= n2% ------------------------------------------% [x,n] = stepseq(n0,n1,n2)%if ((n0 < n1) || (n0 > n2) || (n1 > n2))error('arguments must satisfy n1 <= n0 <= n2')endn = n1:n2;%x = [zeros(1,(n0-n1)), ones(1,(n2-n0+1))];x = (n-n0) >= 0;2.3调用方式
[x,n]=stepseq(2,-2,7);
% n=[-2,-1,0,1,2,3,4,5,6,7]
% x=1x10 logical
stem(n,x,"filled","r")
2.4调用结果

3.矩形序列
3.1函数

3.2 实现代码
function [x,n]=rectseq(n1,n2,N)
% 个人编写可能有误if n1>=0||n2<n1||n2<N||N<=0error("输入的格式错误");endn=n1:n2;% x=[zeros(1,0-n1),ones(1,N),zeros(1,n2-N+1)];x=bitand(n>=0,n<N);
end
3.3调用方式
[x,n]=rectseq(-2,5,4);
% n=[-2,-1,0,1,2,3,4,5]
% x=1x8 logical
stem(n,x,"filled")
3.4 调用结果

4.实指数序列
4.1函数

4.2实现代码
function [x,n]=realexpseq(n1,n2,a)
% 个人编写
if n1>n2error("n1应该小于n2");
endn=n1:n2;an=a.^n;x=an.*stepseq(0,n1,n2);
end
4.3调用方式
[x,n]=realexpseq(-4,5,2);
% n=[-4,-3,-2,-1,0,1,2,3,4,5]
% x=[0,0,0,0,1,2,4,8,16,32]
stem(n,x,"r")
4.4调用结果

5.正弦型序列
5.1函数

5.2实现代码
function [x,n]=sinseq(n1,n2,w,w0)
%该函数表示sin(w*n+w0)
if n1>n2error("n1应该小于n2");
end
n=n1:n2;
x=sin(w*n+w0);
end
5.3调用方式
[x,n]=sinseq(-pi*2,2*pi,1,0);
% n=1x13 double
% x=1x13 double
stem(n,x,'filled')
5.4调用结果

6.复指数序列
6.1函数

6.2实现代码
function [x,n]=comexpseq(n1,n2,a,w0)
n=n1:n2;
x=exp((a+1i*w0).*n);
end
6.3调用方式
[x,n]=comexpseq(-2,5,2,1);
subplot(2,1,1);
stem(n,real(x),"filled")
xlabel("n");
ylabel("实部")
subplot(2,1,2);
stem(n,imag(x),"filled")
xlabel("n")
ylabel("虚部")
6.4调用结果

备注
以上函数部分是自己写的,部分是以封装好的,可能有些的不足的地方,欢迎批评指正
7.序列的简单运算
7.1序列相加
将两个序列对应位置直接相加即可
7.1.1 代码实现
function [y,n]=seqadd(x1,x2,n1,n2)n=min([n1,n2]):max([n1,n2]);% 将相加的序列扩展至相同长度y1=zeros(1,length(n));y2=y1;y1((n>=min(n1))&(n<=max(n1))==1)=x1;y2((n>=min(n2))&(n<=max(n2))==1)=x2;y=y1+y2;
end
7.1.2 调用测试
x1=[2 3 1 4];
n1=-1:2;
x2=[1 2 4];
n2=1:3;
subplot(3,1,1);
stem(n1,x1,"filled",'b')
xlim([min([n1,n2]) max([n1,n2])])
subplot(3,1,2)
stem(n2,x2,'filled',"g");
xlim([min([n1,n2]) max([n1,n2])])
[y,n]=seqadd(x1,x2,n1,n2);
subplot(3,1,3)
stem(n,y,"filled","r");
xlim([min([n1,n2]) max([n1,n2])])
7.1.3 调用结果

7.2序列相乘
将两个序列对应位置直接相乘即可
7.2.1 代码实现
function [y,n]=seqmul(x1,x2,n1,n2)
n=min([n1,n2]):max([n1,n2]);
y1=zeros(1,length(n));
y2=y1;
y1((n>=min(n1)&n<=max(n1))==1)=x1;
y2((n>=min(n2)&n<=max(n2))==1)=x2;
y=y1.*y2;
end7.2.2 调用测试
x1=[2 3 1 4];
n1=-1:2;
x2=[1 2 4];
n2=1:3;
subplot(3,1,1);
stem(n1,x1,"filled",'b')
xlim([min([n1,n2]) max([n1,n2])])
subplot(3,1,2)
stem(n2,x2,'filled',"g");
xlim([min([n1,n2]) max([n1,n2])])
[y,n]=seqmul(x1,x2,n1,n2);
subplot(3,1,3)
stem(n,y,"filled","r");
xlim([min([n1,n2]) max([n1,n2])])
7.2.3 调用结果

7.3序列移位
将序列左移或者右移
7.3.1 代码实现
function [y,n]=seqshift(x,n,m)
% 将序列向左移m位
% y=x(n-m)
n=n-m;
y=x;
end
7.3.2 调用测试
x=[2 4 3 5];
n=1:4;
subplot(2,1,1)
stem(n,x,'filled','g')
xlim([-5,5])
[y,n]=seqshift(x,n,3);
subplot(2,1,2);
stem(n,y,"filled",'r');
xlim([-5,5])
7.3.3 调用结果

7.4 序列翻褶
将序列沿着原点翻褶
7.4.1 代码实现
function [y,n]=seqfold(x,n)
n=-max(n):-min(n);
y=zeros(1,length(x));
for i=1:length(x)y(length(n)-i+1)=x(i);
end
7.4.2 调用测试
x=[4 2 5 3];
n=-1:2;
subplot(2,1,1);
stem(n,x,"filled",'g');
xlim([-4 4])
[y,n]=seqfold(x,n);
subplot(2,1,2);
stem(n,y,'filled','r');
xlim([-4 4])7.4.3 调用结果

结语
上述函数虽然在Signal Processing Toolbox中都有提供,后续只要会使用即可,本篇博客为了帮助初学者更好的理解各种序列和运算实现的底层过程,为后续学习基于matlab仿真的数字信号处理打下良好的基础。上述代码可能有部分编写不足之处,欢迎批评指出!
相关文章:

离散时间信号的产生
文章目录 前言1.单位冲激序列函数1.2 函数:1.3 实现代码:1.3 调用方式1.4 调用结果 2.单位阶跃序列函数2.1 函数2.2实现代码2.3调用方式2.4调用结果 3.矩形序列3.1函数3.2 实现代码3.3调用方式3.4 调用结果 4.实指数序列4.1函数4.2实现代码4.3调用方式4.…...
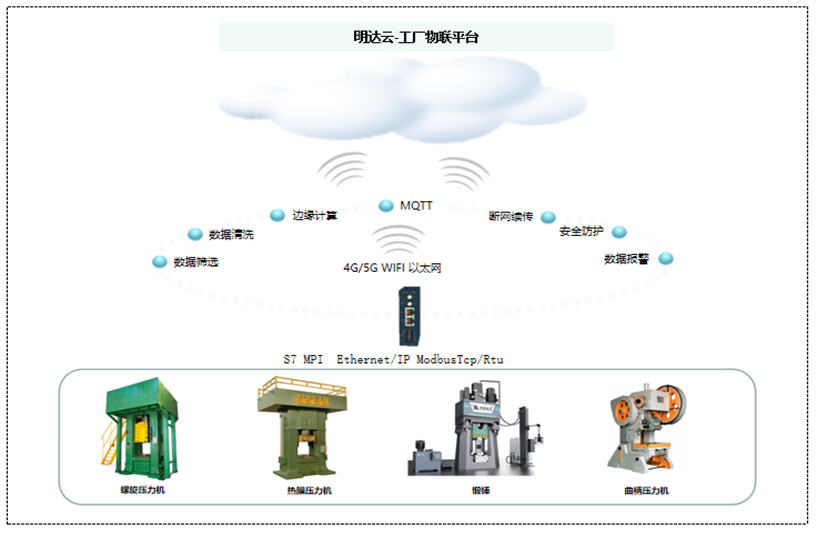
物联优化汽车齿轮锻造
在汽车齿轮的锻造工艺中,锻造温度、锻造压力与行程、锻造速度与锤击方式以及热处理工艺等核心参数扮演着举足轻重的角色。这些参数的精准控制与实时监测,对于提升生产效率、确保产品质量、削减生产成本以及推动生产智能化转型具有不可估量的价值。明达技…...

CocosCreator 构建透明背景应用(最新版!!!)
文章目录 透明原理补充设置截图以及代码step1: electron-js mian.jsstep2:ENABLE_TRANSPARENT_CANVASstep3:SOLID_COLOR Transparentstep:4 Build Web phonestep5:package electron-js & change body background-color 效果图补充 透明原理 使用Cocos creator 做桌面应用开…...

使用CentOS宝塔面板docker搭建EasyTier内网穿透服务
0. 前言 EasyTier是一个简单、安全、去中心化的内网穿透 VPN 组网方案,部署方便,支持 MacOS/Linux/Windows/FreeBSD/Android平台,而且作者搭建了一个公共服务器,不想折腾自建服务,可以使用默认的公共服务器地址 tcp:/…...

HTMLCSS: 实现可爱的冰墩墩
效果演示 HTML <div class"wrap"><div class"body"></div><div class"ear"></div><div class"ear rightEar"></div><div class"leftHand"></div><div class"…...

天地图入门|标注|移动飞行|缩放,商用地图替换
“天地图”是国家测绘地理信息局建设的地理信息综合服务网站。集成了来自国家、省、市(县)各级测绘地理信息部门,以及相关政府部门、企事业单位 、社会团体、公众的地理信息公共服务资源,如果做的项目是政府部门、企事业单位尽量选…...

Flutter PC端UI组件库
一、参考Element-ui的设计和交互,构建基于dart的Flutter UI组件库 https://javonhuang.github.io/sky-ui-page/index.html...

NVR小程序接入平台/设备EasyNVR多品牌NVR管理工具/设备汇聚公共资源场景方案全析
随着信息技术的飞速发展,视频监控已经成为现代社会安全管理和业务运营不可或缺的一部分。特别是在公共资源管理方面,视频监控的应用日益广泛,涵盖了智慧城市、智能交通、大型企业以及校园安防等多个领域。NVR小程序接入平台EasyNVR作为一款功…...
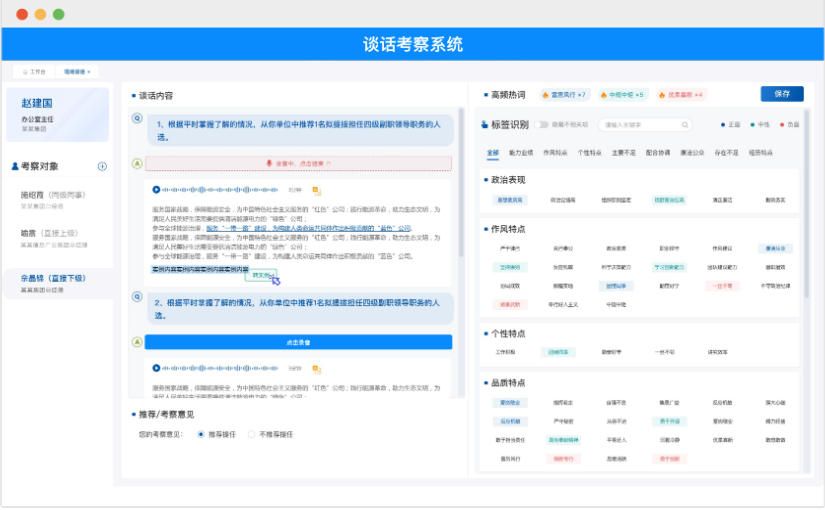
干部谈话考察系统:革新传统,精准高效
在干部选拔任用和考核评价的过程中,谈话考察一直是关键环节之一。然而,传统的谈话考察方式却面临着诸多痛点,严重影响了干部考察工作的质量和效率。干部谈话考察系统的出现,为解决这些问题提供了有力的武器。 一、传统谈话考察的…...
)
反转链表(Leetcode)
反转链表 Leetcode题目链接 题意:翻转一个单链表 🌰: 输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL 在链表本身进行反转即可,不用重新定义链表,这同时浪费时间和空间。 需要采用哑…...

制作游戏外挂的技术栈有哪些
制作游戏外挂是一项涉及多方面技术的复杂任务。这项技术通常被用于在游戏中获得不公平的优势,因此也遭到了大量的讨论与争议。制作外挂需要深厚的编程基础、对系统底层的深入理解以及对具体游戏架构的详细研究。以下是一篇全面的分析文章,旨在揭示制作游…...

python下载pdf
要下载 PDF 文件并将其保存到本地文件夹中,你可以使用 Python 的 requests 库来发送 HTTP 请求,并使用 os 和 io 库来处理文件操作。以下是一个示例代码,展示了如何从给定的 URL 下载 PDF 文件并将其保存到本地 data 文件夹中: i…...

我们来学mysql -- 同时使用 AND 和 OR 查询错误(填坑篇)
AND 和 OR 一同使用问题 现象分析处理扩展 现象 业务上在“锁定”当前零件所在出口国的所有零件时,出现其他国家零件 问题定位 分析 or 切断了操作符之间的连续性,从union角度分析 where k1 Td621 and k1 Vda96 or k3 P00009等同 select * fr…...

关于Websocket
Websocket的基本概念 Websocket是一个“应用层协议”,和HTTP地位是对等的。都是基于传输层的TCP实现的一个广泛被使用的应用层协议。这个协议可以实现服务器主动给客户端推送数据这样的功能。 websocket报文格式 简单了解一下Websocket的报文格式: FIN表…...

vue2 pdf 链接地址打开
vue2 pdf 链接地址打开 1、先下载依赖 “vue-pdf”: “^4.3.0”, “pdfh5”: “^1.4.0”, “pdfjs-dist”: “2.5.207”, 3、打开pdf <template><div id"app"><div id"demo"></div></div> </template> <script&g…...

c# 动态lambda实现二级过滤(多种参数类型)
效果 调用方法 实体类(可以根据需求更换) public class ToolStr50 {public bool isSelected { get; set; }public string toolStr1 { get; set; }public string toolStr2 { get; set; }public string toolStr3 { get; set; }public string toolStr4 { …...

34.Redis事务
1.事务Redis介绍 事务表示一组动作,要么全部执行,要么全部不执行。 例如微博粉丝关注用户,博主粉丝列表增加了用户,粉丝关注列表增加了博主; Redis 提供了简单的事务功能,将一组需要一起执行的命令放到mult…...

认识类和对象
认识类 类是用来对一个实体 ( 对象 ) 来进行描述的,主要描述该实体(对象)具有哪些属性(外观尺寸等),哪些功能(用来干啥) 类中包含的内容称为 类的成员。属性主要是用来描述类的,称之为 类的成员属性或者 类成员变量。方法主要说明类具有哪些功…...

解决echarts桑基图为0时tooltip不显示的问题
关键代码 formatter: function (params) {console.log("params",params)if (params.value 0) {// 如果值为0,返回空字符串,不显示任何内容return params.name : params.value;// return ;} else {// 否则返回标准的格式化信息return par…...

vue3 基础笔记
基础模板语法 //1. 普通文本插值: <p>{{ rawHtml }}</p>//2. v-html 指令:插入 HTML 内容,并希望 Vue 将其视为 HTML 而不是纯文本 <p v-html"rawHtml"></p> let rawHtml <span>这是一个 <b>HTML</…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
