快速傅里叶变换(FFT)基础(附python实现)
对于非专业人士,傅里叶变换一直是一个神秘的武器,它可以分析出不同频域的信息,从时域转换到频域,揭示了信号的频率成分,对于数字信号处理(DSP)、图像、语音等数据来说,傅里叶变换是最为基础,同时非常重要的分析工具。在处理真实世界的问题中,快速傅里叶变换(Fast Fourier Transform,FFT)是一种高效的算法,用于计算离散傅里叶变换(Discrete Fourier Transform,DFT)及其逆变换。DFT是傅里叶变换在离散数据上的版本,FFT算法的出现极大地减少了DFT的计算复杂度,使得在实际应用中变得可行。本文介绍一些基础概念,最后使用一个python小例子来展示FFT的效果。
傅里叶变换的基本概念
傅里叶变换是一种数学工具,它表明任何周期函数都可以表示为正弦和余弦函数的和。在信号处理中,傅里叶变换用于分析信号的频率成分,即信号中包含的所有不同频率的正弦波。
离散傅里叶变换(DFT)
DFT是傅里叶变换的离散版本,它将有限长度的时域信号转换为有限长度的频域信号。对于一个长度为N的序列x[n],其DFT定义为:
[ X [ k ] = ∑ n = 0 N − 1 x [ n ] ⋅ e − j 2 π N k n ] [ X[k] = \sum_{n=0}{N-1} x[n] \cdot e{-j \frac{2\pi}{N} kn} ] [X[k]=∑n=0N−1x[n]⋅e−jN2πkn]
其中,X[k]是序列x[n]的DFT,k是频率索引,j是虚数单位。
快速傅里叶变换(FFT)
FFT是DFT的一种高效算法实现,它利用了DFT的对称性和周期性等数学性质,将复杂度从 O ( N 2 ) O(N^2) O(N2)降低到 O ( N l o g N ) O(N log N) O(NlogN)。这意味着对于长度为N的序列,FFT算法可以在对数时间内完成DFT的计算。
FFT的关键性质
FFT是一种强大的工具,它使得在各种科学和工程领域中分析和处理信号成为可能。通过将信号分解为不同频率的组成部分,FFT揭示了信号的内在结构,为信号处理提供了一个强大的分析框架。所有这些,其实都利益于它具备如下的特点:
- 线性:FFT保持了傅里叶变换的线性性质。
- 时域和频域的局部性:FFT算法利用了“蝶形操作”来减少复数乘法的数量。
- 并行性:FFT可以并行执行,进一步提高计算效率。
因此,FFT在很有领域有广泛的应用:
- 信号处理:音频和图像的压缩、滤波和分析。
- 图像处理:边缘检测、图像增强和图像压缩。
- 通信系统:在无线通信中,FFT用于信道均衡和信号调制。
- 数据分析:频谱分析和周期性检测。
代码
下面给出一个例子,使用pytorch,分析两个不同频率合成后的信号,使用FFT识别出两个频率,最后使用matplotlib来进行可视化:
import torch
import numpy as np
import matplotlib.pyplot as plt# 设置参数
sample_rate = 1000 # 采样率 (Hz)
T = 1 / sample_rate # 采样间隔
t = np.linspace(0, 1, sample_rate, endpoint=False) # 时间向量# 生成信号
freq1, freq2 = 50, 120 # 两正弦波的频率
amplitude1, amplitude2 = 0.7, 0.5 # 振幅
signal = amplitude1 * np.sin(2 * np.pi * freq1 * t) + amplitude2 * np.sin(2 * np.pi * freq2 * t)# 将信号转换为 Torch 张量
signal_tensor = torch.tensor(signal, dtype=torch.float32)# 执行 RFFT
rfft_result = torch.fft.rfft(signal_tensor)# 获取幅度谱
magnitude = torch.abs(rfft_result)# 频率轴
frequencies = torch.fft.rfftfreq(signal.size, d=T)plt.figure(figsize=(12, 6))# 原始信号
plt.subplot(2, 1, 1)
plt.plot(t, signal)
plt.title('Original Signal')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')# 频谱
plt.subplot(2, 1, 2)
plt.plot(frequencies.numpy(), magnitude.numpy())
plt.title('Magnitude Spectrum')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Magnitude')plt.tight_layout()
plt.show()
效果
上图为原始信息,由两个信息合成;下图为解析出来的光谱图,可以看到,分析得到两个脉冲,分别对应两个正弦波的频率:50与120,可以看到FFT的神奇之处了吧:)

相关文章:

快速傅里叶变换(FFT)基础(附python实现)
对于非专业人士,傅里叶变换一直是一个神秘的武器,它可以分析出不同频域的信息,从时域转换到频域,揭示了信号的频率成分,对于数字信号处理(DSP)、图像、语音等数据来说,傅里叶变换是最…...

使用Docker-compose安装mysql5.7
1.首先选择一个目录用来存放docker-compse文件以及mysql的数据(例如logs、conf) cd /home mkdir mysql vi docker-compose.yml2.填写docker-compse.yml内容 version : 3 services:mysql:# 容器名(以后的控制都通过这个)container_name: mysql# 重启策略…...

如何管理PHP的API部署环境
管理PHP的API部署环境是一个涉及多个步骤和考虑因素的过程。以下是一些关键步骤和最佳实践,用于管理PHP的API部署环境: 一、选择合适的服务器和配置环境 选择服务器:根据API的访问量和性能需求,选择合适的服务器。可以选择物理服…...

web——sqliabs靶场——第一关
今天开始搞这个靶场,从小白开始一点点学习,加油!!!! 1.搭建靶场 注意点:1.php的版本问题,要用老版本 2.小p要先改数据库的密码,否则一直显示链接不上数据库 2.第一道题࿰…...

tartanvo ubuntu 20.04部署
1. 所有环境安装流程参考 2. 运行python3 tartanvo_node.py出现问题: ImportError: cannot import name int from numpy版本问题,卸载当前版本并更换版本: pip uninstall numpy pip install numpy1.22.4问题解决。 3. 采用2to3脚本将其代…...
)
SpringBoot整合Freemarker(三)
定义循环输出的宏 <#macro list title items> ${title?cap_first}:<#list items as x>*${x?cap_first}</#list> </#macro><list items["mouse", "elephant", "python"] title"Animals"/> 输出结果…...

Android 一个APP打开另一个app的两种方式,需添加QUERY_ALL_PACKAGES权限
加<uses-permission android:name"android.permission.QUERY_ALL_PACKAGES"/> 方式1:打开外部app,在新窗口打开。 private void doStartAppPackageName(String packagename) { // 通过包名获取此APP详细信息&#x…...

<数据集>草莓叶片病害识别数据集<目标检测>
数据集格式:VOCYOLO格式 图片数量:4371张 标注数量(xml文件个数):4371 标注数量(txt文件个数):4371 标注类别数:7 标注类别名称:[Angular Leafspot, Anthracnose Fruit Rot, Blossom Blight, Gray Mol…...

React 中 `key` 属性的警告及其解决方案
React 中 key 属性的警告及其解决方案 文章目录 React 中 key 属性的警告及其解决方案1. 引言2. 什么是 key 属性3. key 属性的重要性4. 常见的 key 属性警告及其原因4.1 缺少 key 属性4.2 使用不稳定的 key(如索引)4.3 重复的 key 值 5. 如何解决 key 属…...
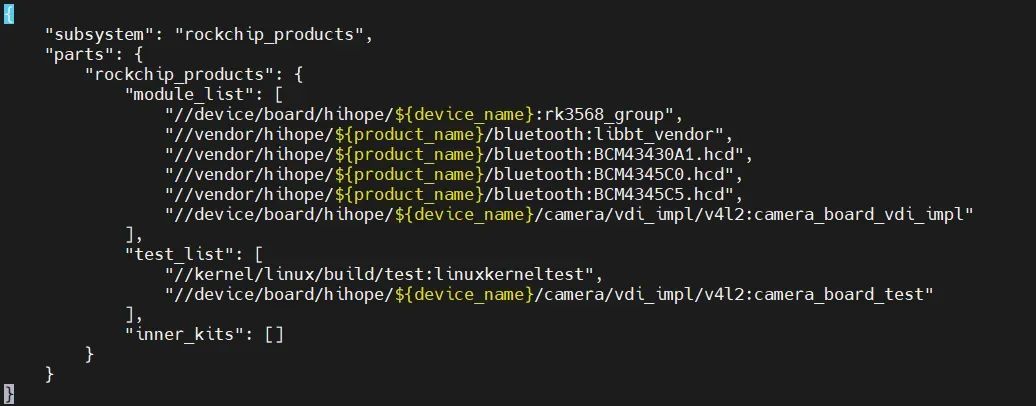
OpenHarmony4.1蓝牙芯片如何适配?触觉智能RK3568主板SBC3568演示
当打开蓝牙后没有反应时,需要排查蓝牙节点是否对应、固件是否加载成功,本文介绍开源鸿蒙OpenHarmony4.1系统下适配蓝牙的方法,触觉智能SBC3568主板演示 修改对应节点 开发板蓝牙硬件连接为UART1,修改对应的节点,路径为…...

濮良贵《机械设计》第十版课后习题答案全解PDF电子版
《机械设计》(第十版)是“十二五”普通高等教育本科国家级规划教材, 是在《机械设计》(第九版)的基础上修订而成的。本次修订主要做了以下几项工作: 1. 内容的适当更新——自本书第九版出版以来, 机械工程及相关领域的新理论、新技术和新标准…...

Python进阶语法探索:列表推导式
在Python编程中,列表推导式(List Comprehensions)是一种简洁而强大的语法结构,它允许你以一行代码的形式创建列表,同时执行循环、条件判断等操作。列表推导式不仅提高了代码的可读性,还显著提升了编程效率。…...

java合并图片与文字
通过java来绘制海报,加载外部字体并设置样式大小与加粗、设置背景图、合并图片,下面是示例 import javax.imageio.ImageIO; import java.awt.Color; import java.awt.Font; import java.awt.FontMetrics; import java.awt.Graphics2D; import java.awt.…...

OpenCV快速入门
OpenCV(Open Source Computer Vision Library,开源计算机视觉库)是一个广泛应用于图像处理、计算机视觉、视频分析等领域的开源库。它不仅适用于研究人员和开发人员,还被广泛用于学术、工业和商业应用。本篇文章将帮助你快速了解 …...

ArcGIS软件之“计算面积几何”地图制作
一、消防站的泰森多边形 效果图: 二、人口调查的泰森多边形 确定后效果图: 三、人口调查的泰森多边形属性设置 确定后的效果图: 四、计算面积几何,用于求密度 先添加字段area_1,然后设置浮点型及字段属性 五…...

RHCE 第四次作业
一.搭建dns服务器能够对自定义的正向或者反向域完成数据解析查询。 1.配置环境 [rootlocalhost ~]# yum install bind [rootlocalhost ~]#systemctl stop firewalld [rootlocalhost ~]#setenforce 0 2.配置DNS主服务器 [rootlocalhost ~]# vim /etc/named.conf options { …...

【贪心算法】No.1---贪心算法(1)
文章目录 前言一、贪心算法:二、贪心算法示例:1.1 柠檬⽔找零1.2 将数组和减半的最少操作次数1.3 最⼤数1.4 摆动序列1.5 最⻓递增⼦序列1.6 递增的三元⼦序列 前言 👧个人主页:小沈YO. 😚小编介绍:欢迎来到…...

分布式光伏管理办法
随着分布式光伏项目的不断增加,传统的管理方式已经难以满足高效、精准的管理需求。光伏业务管理系统作为一种集信息化、智能化于一体的管理工具,正在逐步成为分布式光伏项目管理的重要支撑。 光伏业务管理系统通过数字化手段实现对光伏业务全流程的精细化…...

2024最新软件测试面试热点问题
🍅 点击文末小卡片 ,免费获取软件测试全套资料,资料在手,涨薪更快 大厂面试热点问题 1、测试人员需要何时参加需求分析? 如果条件循序 原则上来说 是越早介入需求分析越好 因为测试人员对需求理解越深刻 对测试工…...

如何利用探商宝精准营销,抓住行业机遇——以AI技术与大数据推动企业信息精准筛选
近年来,随着人工智能与大数据技术的迅猛发展,企业的营销手段和策略发生了巨大变化。尤其是在信息爆炸的数字时代,如何有效利用这些技术在海量数据中精准找到潜在客户,已成为中小企业亟待解决的核心问题。 最近,全球人…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
