二叉树的性质与推导及常见习题整理

目录

一、性质推导 

二、常见的二叉树性质习题

1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（）。

2.在具有 2n 个结点的完全二叉树中，叶子结点个数为（）。

3.一个具有767个节点的完全二叉树，其叶子节点个数为（）。

4.一棵完全二叉树的节点数为531个，那么这棵树的高度为（）。

5.在一颗度为3的树中，度为3的结点有2个，度为2的结点有1个，度为1的结点有2个，则叶子结点有（ ）个。

6.一颗拥有1000个结点的树度为4，则它的最小深度是（ ）。

7.在一颗完全二叉树中，某一个结点没有其左孩子，则该结点一定（ ）。

---

一、性质推导 

1. 若一个二叉树有n个节点，则该二叉树共有(n-1)条边。

推导：如图，可以理解为二叉树除了根节点外，每一个节点头上都有一条边指向它。因此，边的总数就是n-1

2. 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有 2^(i-1)  (i>0)个结点。

推导：当第i层满的时候，就是该层节点数最多的时候。如下图的完全二叉树，第一层最多1个节点，第二层最多2个节点，第三层最多4个节点，第四层最多8个节点……可以归纳出规律：第i层最多2^(i-1)个节点。 

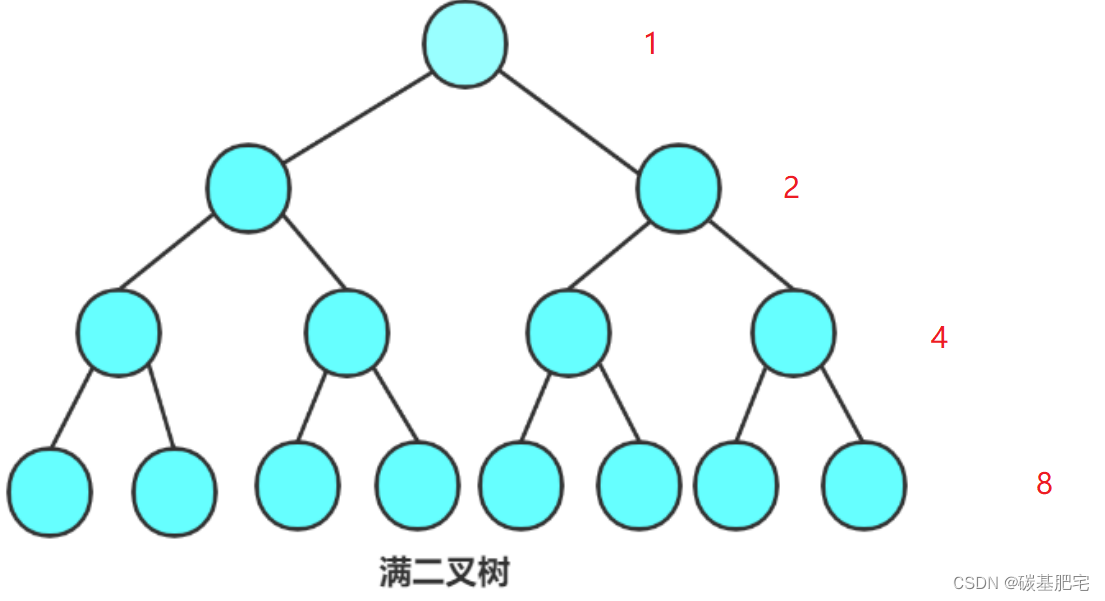
 3. 若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是 2^k -1

(k>=0)

推导：深度为K的二叉树最大节点的情况是该树为一棵满二叉树。将每一层节点数求和，即该树的总结点数。求和的过程是等比数列的求和过程，根据等比数列求和的公式（其中n是项数）：

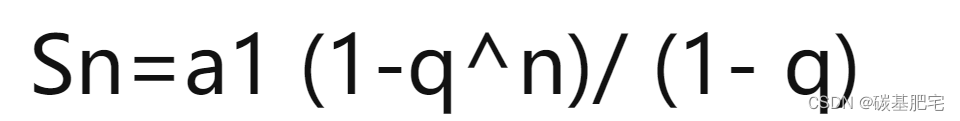
 代入a1（首项）为2^0即1，q为2，n为k，可得最大节点数为： 2^k-1

4. 具有n个结点的完全二叉树的深度k为log(n+1)上取整。

推导：由性质3倒推可得：

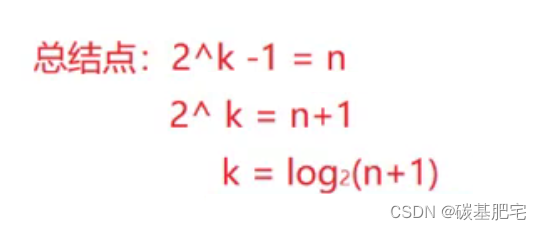
向上取整即若一个数是3点几，则答案向上取4。

假设共有16个节点，n=16.则：2^k = 17，而2^4为16，2^5为32，因此k实际为4点几，但若k取4，则不够，还多了一个节点。因此k应当向上取5.

注意：这里的 k 还有另一种表示方式，即log(n)+1。此时 k 为log(n)+1向下取整。向下取整即3点几向下取3.

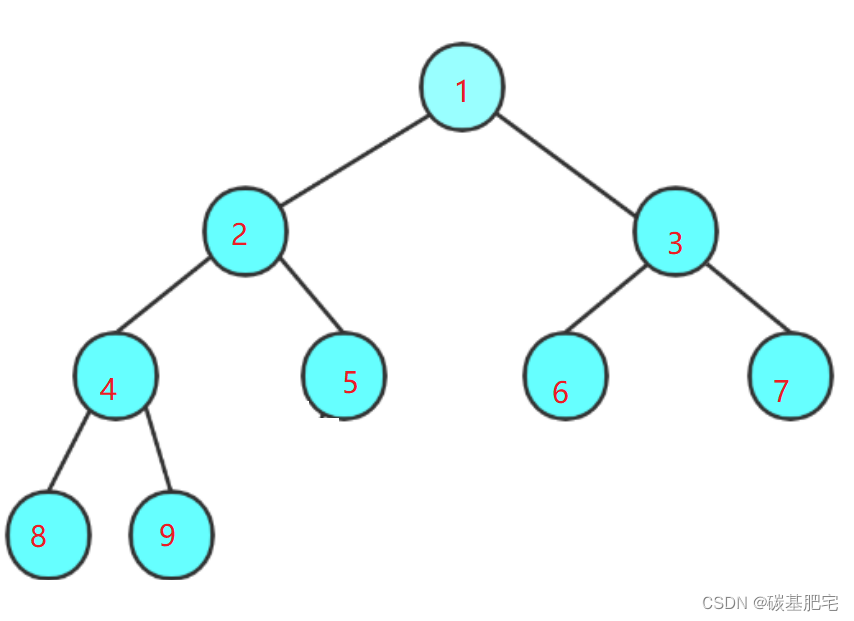
5. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1 （度为0的节点个数比度为2的节点个数多一个。）

推导：该结论的推导运用到了二叉树边与节点个数的关系。

假设度为0的节点有n0个，度为1的节点有n1个，度为2的节点有n2个，总结点数为N。首先可得：N = n0 + n1 + n2 ……①（节点个数关系）

同时，由性质1可得，该二叉树有N-1条边。度为0的节点发射出0条边，度为1的节点发射出1条边，度为2的节点发射出2条边。由此可得：

N-1 = 0*n0 + 1*n1 + 2*n2 ……②（边条数关系）

由①和②可得结论：n0 = n2 + 1

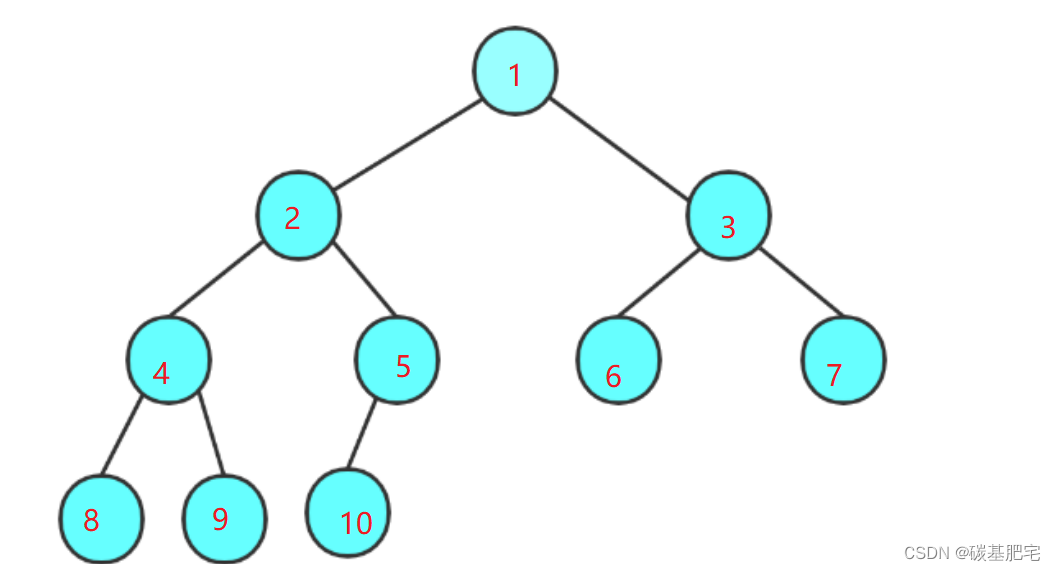
6. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为 i 的结点有：

        若i>0，则其双亲结点序号为：(i-1)/2；若i=0，i为根结点编号，无双亲结点。

        若2i+1<n，则其左孩子序号为：2i+1；否则无左孩子。

        若2i+2<n，则其右孩子序号：2i+2；否则无右孩子。

推导：如下图规律所示。

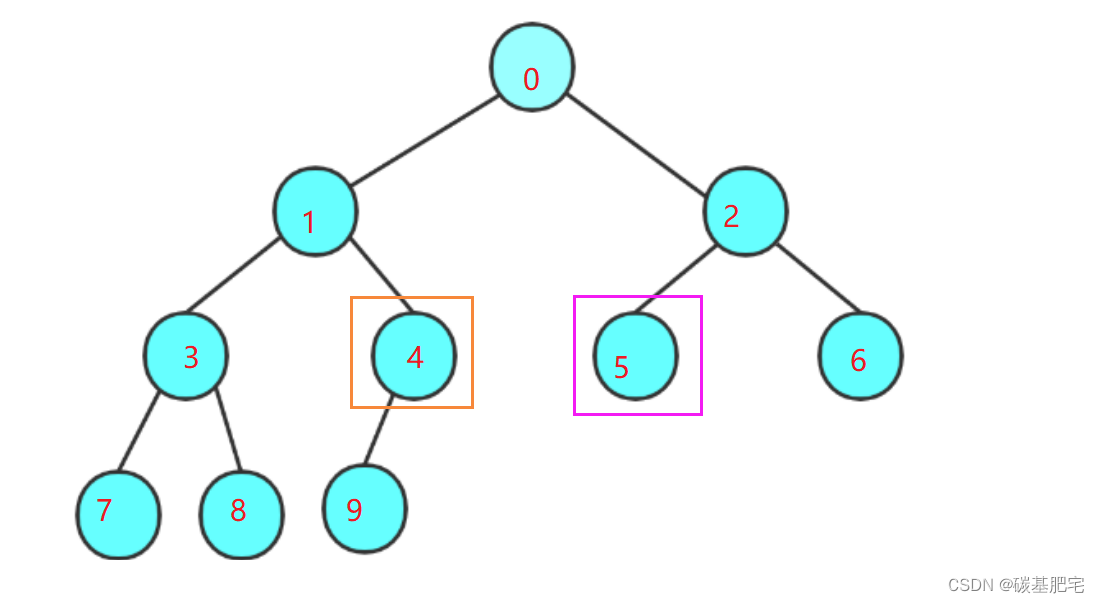
若 i = 4，则其双亲序号为 (i-1)/2 即 (4-1)/2 为1；

左孩子2*i+1为9 < 总结点个数10，因此左孩子存在且序号为9；

右孩子2*i+2为10，不小于10，因此右孩子不存在。

若i = 5，则其双亲序号为(i-1)/2 即 2；

左孩子2*i+1为11大于10，因此左孩子不存在。由于该性质是针对完全二叉树的，因此其右孩子一定也不存在。

注意：若从1开始编号，则序号为i的节点的双亲节点序号为 i/2，左孩子节点为 2*i ，右孩子节点为 2*i + 1.

该结论可以不死记硬背，遇到的时候简单画图即可快速推导。

二、常见的二叉树性质习题

1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（）。

A、不存在这样的二叉树

B、200

C、198

D、199

答案选B。

由性质5可知，n0 = n2+1.n0 = 199+1 = 200

2.在具有 2n 个结点的完全二叉树中，叶子结点个数为（）。

A n

B n+1

C n-1

D n/2

答案选A。

该题运用到了性质5.

首先分析题干，如何求叶子节点的个数？和节点个数相关的公式有二：

n0 = n2 + 1，N = n0 + n1 + n2

已知总个数N为2n，那么只要知道n1即可求出n0.

这里有一个重要的结论：

在完全二叉树中，如果节点总个数为奇数，则没有度为1的节点；如果节点总个数为偶数，只有一个度为1的节点。

节点个数是偶数，只有一个度为1的节点

节点个数是奇数，没有度为1的节点

2n为偶数，因此有一个度为1的节点。

2n = n0 + 1 + n2 = n0 + 1 + n0 - 1

2n = 2n0

n0 = n，故选A

3.一个具有767个节点的完全二叉树，其叶子节点个数为（）。

A 383

B 384

C 385

D 386

答案选B。

本题同上。此时共有奇数个节点，因此没有度为1的节点，即n1 = 0.

由 N = n0 + n1 + n2得： 767 = n0 + 0 + n0 - 1

n0 = 768/2 = 384

4.一棵完全二叉树的节点数为531个，那么这棵树的高度为（）。

A 11

B 10

C 8

D 12

答案选B。

已知节点求高度，运用性质4，h = log(n+1)向上取证。h = log(531+1)，向上取整为10，故选B。

5.在一颗度为3的树中，度为3的结点有2个，度为2的结点有1个，度为1的结点有2个，则叶子结点有（ ）个。

A.4

B.5

C.6

D.7

本题选C。

运用了边与节点个数的关系。

令n3 = 2；n2 = 1；n1 = 2；设总结点的个数为N

则由节点个数的关系得 N = n3 + n2 + n1 + n0，由边条数的关系得 N-1 = 3*n3 + 2*n2 + 1*n1 + 0*n0

联立可得：N = 2 + 1 + 2 + n0，N-1 = 3*2 + 2*1 + 1*2 + 0

n0 = 6

6.一颗拥有1000个结点的树度为4，则它的最小深度是（ ）。

A.5

B.6

C.7

D.8

答案选B

当这棵树每一层都是满的时，它的深度最小。也就是说，这棵树应当是一棵满四叉树。

假设高度为h，则由求二叉树节点个数的公式类比可知：根据等比数列求和公式得，这个数的节点个数为(4^h - 1) / 3

当h = 5，最大节点数为341，当h = 6， 最大节点数为1365，所以，最小深度应该向上取整为6。

7.在一颗完全二叉树中，某一个结点没有其左孩子，则该结点一定（ ）。

A.是根结点

B.是叶结点

C.是分支结点

D.在倒数第二层

答案选B.

完全二叉树中，如果一个节点没有左孩子，则一定没有右孩子，它必定为一个叶子节点。

最后一层一定为叶子节点，但是倒数第二层也可能存在叶子节点。