第13章 聚合函数
一、聚合函数介绍
实际上 SQL 函数还有一类,叫做聚合(或聚集、分组)函数,它是对一组数据进行汇总的函数,输入的是一组数据的集合,输出的是单个值。(可以是一个字段的数据,也可以是通过分组后每一组的数据)。
1.1 常见的聚合函数
| 函数 | 解释 |
| AVG() | 求一组数据的平均值。(不计算null值)(只适用于数值) |
| SUM() | 求一组数据的总和。(不计算null值)(只适用于数值) |
| MAX() | 求一组数据中的最大值。(不计算null值)(适用于数值、字符串、日期时间等任意数据类型) |
| MIN() | 求一组数据的最小值。(不计算null值)(适用于数值、字符串、日期时间等任意数据类型) |
| COUNT() | 求一组数据的个数。(不计算null值)(适用于数值、字符串、日期时间等任意数据类型) |
1.2 聚合函数的语法

注:聚合函数不能嵌套调用。比如不能出现类似“AVG(SUM(字段名称))”形式的调用。
1.3 AVG和SUM函数
只适用于对数值型数据使用AVG 和 SUM 函数。

1.4 MIN和MAX函数
可以对任意数据类型的数据使用 MIN 和 MAX 函数。

1.5 COUNT函数
COUNT(*)返回表中记录总数(或指定字段在查询结果中出现的次数),适用于任意数据类型。
COUNT(expr) 返回expr不为空(null值不计算在内)的记录总数。因为不计算空值,所以expr是字段名时得出的记录总数并不是正确的记录总数。
综上,一共有三种计算记录总数的方式。count(字段)、count(*)、count(1)。其中推荐使用count(*)和count(1)两种方式,其中1表示“并不指明哪一个字段”,相当于拿1来表示每一条记录,当然使用2等任意字符都可以。

问题:用count(*),count(1),count(列名)谁好呢?
其实,对于MyISAM引擎的表是没有区别的,这种引擎内部有一计数器在维护着行数,三者效率相同都是O(1),并且结果也相同。 Innodb引擎的表用count(*),count(1)直接读行数,复杂度是O(n),因为innodb真的要去数一遍,但好于具体的count(列名),故效率:count(*) = count(1) > count(列名)。
问题:能不能使用count(列名)替换count(*)?
不要使用 count(列名)来替代 count(*) , count(*) 是 SQL92 定义的标准统计行数的语法,跟数据库无关,跟 NULL 和非 NULL 无关。 说明:count(*)会统计值为 NULL 的行,而 count(列名)不会统计此列为 NULL 值的行。
AVG = SUM / COUNT 永远成立,因为AVG和SUM也不计算空值。
相关文章:

第13章 聚合函数
一、聚合函数介绍 实际上 SQL 函数还有一类,叫做聚合(或聚集、分组)函数,它是对一组数据进行汇总的函数,输入的是一组数据的集合,输出的是单个值。(可以是一个字段的数据,也可以是通…...
)
【计网不挂科】计算机网络期末考试——【选择题&填空题&判断题&简述题】试卷(4)
前言 大家好吖,欢迎来到 YY 滴计算机网络 系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 本博客主要内容,收纳了一部门基本的计算机网络题目,供yy应对期中考试复习。大家可以参考 本章是去答案版本。带答案的版本在下…...

C# 中 LibraryImport 和 DllImport有什么不同
libraryimport 和 dllimport 是两个与动态链接库(DLL)相关的术语,它们在不同的编程语言和上下文中有不同的含义和用途。 在 C# 中,DllImportAttribute 是一个特性,用于指示一个方法声明是作为对非托管 DLL 中函数的 P…...

PDF编辑工具Adobe Acrobat DC 2023安装教程(附安装包)
Adobe Acrobat DC 2023 是 Adobe 公司推出的一款功能强大的 PDF 文档处理软件。它不仅支持创建、编辑和签署 PDF 文件,还提供了丰富的工具来管理和优化这些文件。以下是 Acrobat DC 2023 的一些主要特点: 1.PDF 创建与编辑:用户可以直接从多…...

系动词、表语和主语补足语
系动词、表语和主语补足语 1. The classification of English verbs (英语动词的分类)2. 系动词 (连系动词)2.1. Grammatical function (语法功能) 3. 表语和主语补足语3.1. Predicative expression (表语)3.2. Subject complement (主语补足语) 4. Copula-like words4.1. List…...
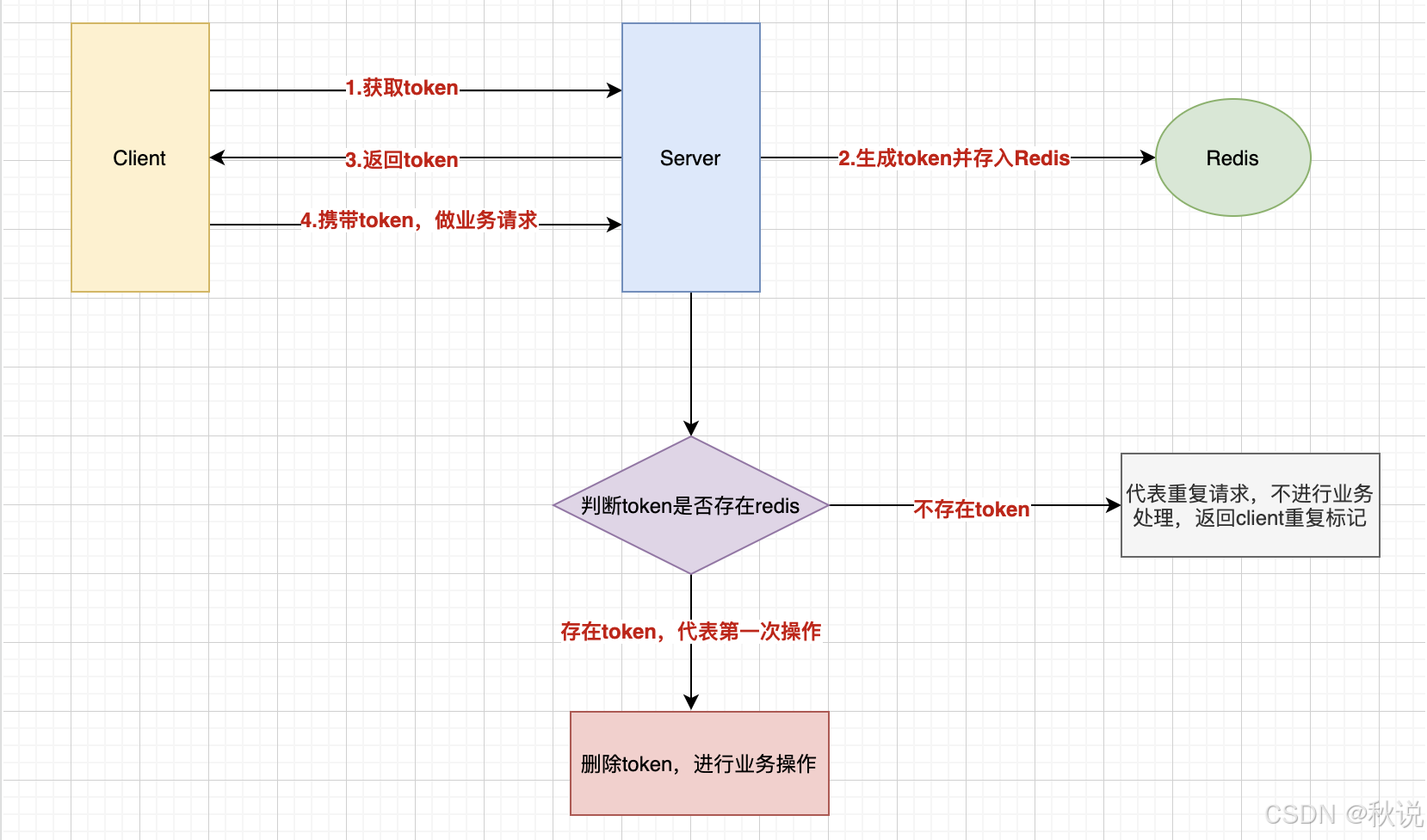
【网络安全 | 并发问题】Nginx重试机制与幂等性问题分析
未经许可,不得转载。 文章目录 业务背景Nginx的错误重试机制proxy_next_upstream指令配置重试500状态码非幂等请求的重试问题幂等性和非幂等性请求non_idempotent选项的使用解决方案业务背景 在现代互联网应用中,高可用性(HA)是确保系统稳定性的关键要求之一。为了应对服务…...

Java 详解 接口
文章目录 一、概述1.1、何为接口1.2、接口的定义 二、特点2.1、接口的成员变量2.2、接口的成员方法2.3、接口中不可以含有构造器和代码块2.4、接口不可以实例化对象2.5、接口和类之间使用implements关键字进行连接2.6、当类在重写接口中的方法时,不可以使用默认的访…...

wordpress搬家迁移后怎么修改数据库用户名
在WordPress中修改数据库用户名,你需要更新WordPress的配置文件wp-config.php。以下是步骤和示例代码: 使用FTP客户端或文件管理器登录到你的网站的主机账户。 找到wp-config.php文件,它通常位于WordPress安装的根目录中。 打开wp-config.…...

C# 用于将一个DataTable转换为Users对象的列表
1:第一种例子: /// <summary> /// 用户名循环赋值 /// </summary> /// <param name"dt"></param> /// <returns></returns> public List<Users> FenPeiFillModelUsers(DataTable dt) { …...

Spark中的shuffle
Shuffle的本质基于磁盘划分来解决分布式大数据量的全局分组、全局排序、重新分区【增大】的问题。 1、Spark的Shuffle设计 Spark Shuffle过程也叫作宽依赖过程,Spark不完全依赖于内存计算,面临以上问题时,也需要Shuffle过程。 2、Spark中哪…...
网络安全SQL初步注入2
六.报错注入 mysql函数 updatexml(1,xpath语法,0) xpath语法常用concat拼接 例如: concat(07e,(查询语句),07e) select table_name from information_schema.tables limit 0,1 七.宽字节注入(如果后台数据库的编码为GBK) url编码:为了防止提交的数据和url中的一些有特殊意…...
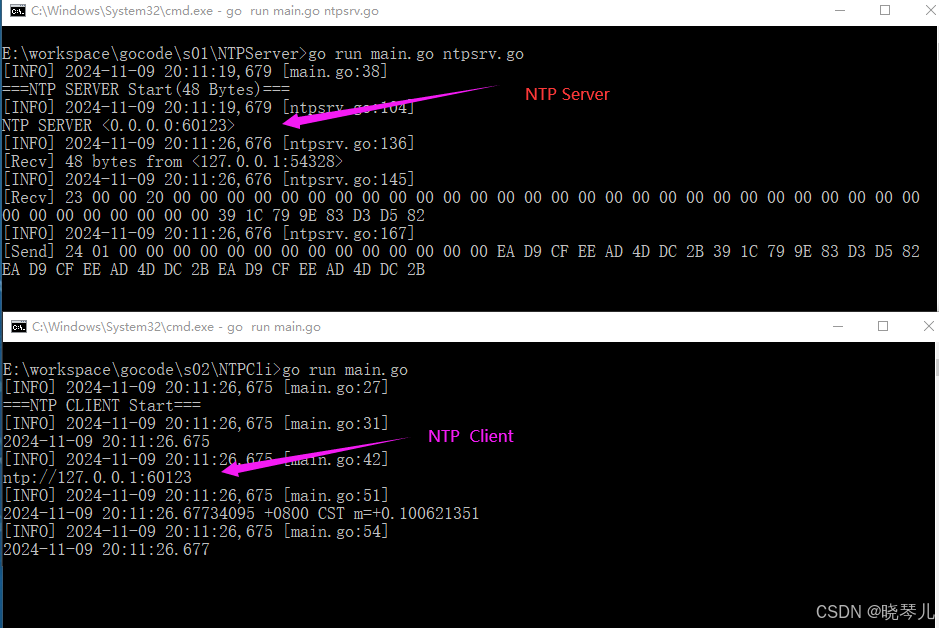
使用Go语言编写一个简单的NTP服务器
NTP服务介绍 NTP服务器【Network Time Protocol(NTP)】是用来使计算机时间同步化的一种协议。 应用场景说明 为了确保封闭局域网内多个服务器的时间同步,我们计划部署一个网络时间同步服务器(NTP服务器)。这一角色将…...

注意力机制篇 | YOLO11改进 | 即插即用的高效多尺度注意力模块EMA
前言:Hello大家好,我是小哥谈。与传统的注意力机制相比,多尺度注意力机制引入了多个尺度的注意力权重,让模型能够更好地理解和处理复杂数据。这种机制通过在不同尺度上捕捉输入数据的特征,让模型同时关注局部细节和全局…...
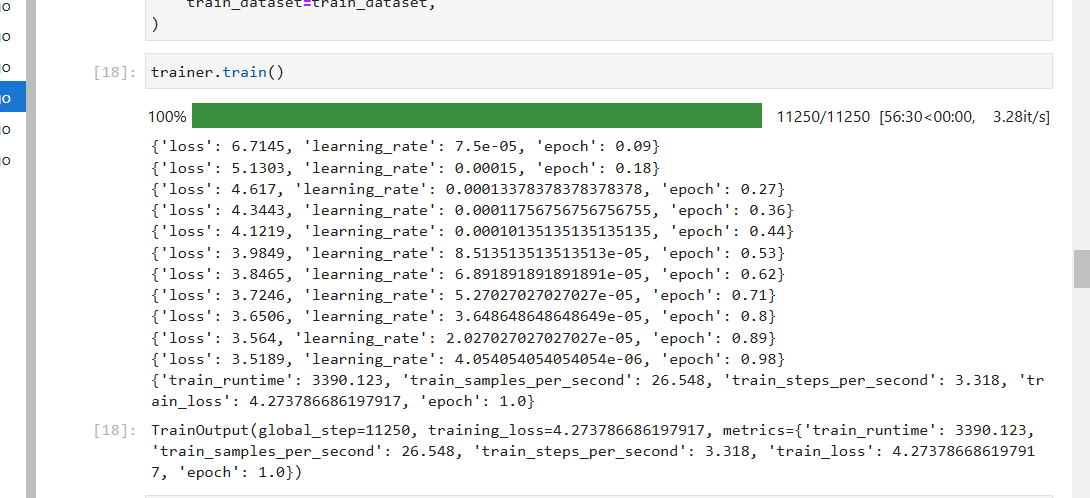
昇思大模型平台打卡体验活动:项目3基于MindSpore的GPT2文本摘要
昇思大模型平台打卡体验活动:项目3基于MindSpore的GPT2文本摘要 1. 环境设置 本项目可以沿用前两个项目的相关环境设置。首先,登陆昇思大模型平台,并进入对应的开发环境: https://xihe.mindspore.cn/my/clouddev 接着࿰…...
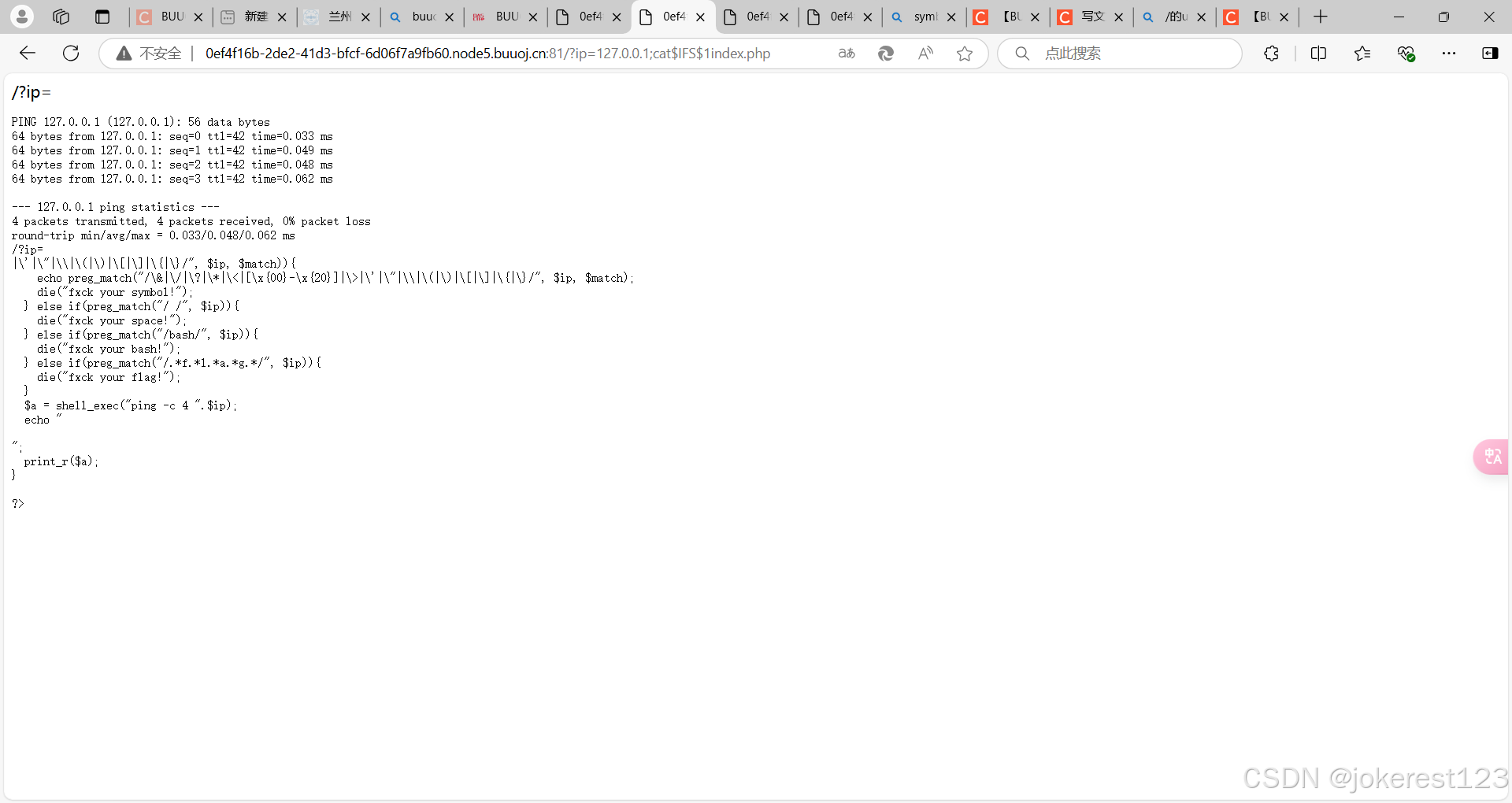
web——[GXYCTF2019]Ping Ping Ping1——过滤和绕过
0x00 考点 0、命令联合执行 ; 前面的执行完执行后面的 | 管道符,上一条命令的输出,作为下一条命令的参数(显示后面的执行结果) || 当前面的执行出错时(为假)执行后面的 & 将任…...

婚礼纪 9.5.57 | 解锁plus权益的全能结婚助手,一键生成结婚请柬
婚礼纪是一款结婚服务全能助手,深受9000万新人信赖的一站式结婚服务平台。解锁plus权益后,用户可以享受部分VIP会员功能。应用提供了丰富的结婚筹备工具和服务,包括一键生成结婚请柬、婚礼策划、婚纱摄影、婚宴预订等。婚礼纪旨在为新人提供全…...

M1M2 MAC安装windows11 虚拟机的全过程
M1/M2 MAC安装windows11 虚拟机的全过程 这两天折腾了一下windows11 arm架构的虚拟机,将途中遇到的坑总结一下。 1、虚拟机软件:vmware fusion 13.6 或者 parallel 19 ? 结论是:用parellel 19。 这两个软件都安装过࿰…...

监控架构-Prometheus-普罗米修斯
目录 1. Prometheus概述 2. Prometheus vs Zabbix 3. Prometheus极速上手指南 3.1 时间同步 3.2 部署Prometheus 3.3 启动Prometheus 3.4 Prometheus监控架构 3.5 补充 配置页面 简单过滤 查看数据 查看图形 http://prometheus.oldboylinux.cn:9090/metrics显示…...

Kylin Server V10 下自动安装并配置Kafka
Kafka是一个分布式的、分区的、多副本的消息发布-订阅系统,它提供了类似于JMS的特性,但在设计上完全不同,它具有消息持久化、高吞吐、分布式、多客户端支持、实时等特性,适用于离线和在线的消息消费,如常规的消息收集、…...

windows环境下cmd窗口打开就进入到对应目录,一般人都不知道~
前言 很久以前,我还在上一家公司的时候,有一次我看到我同事打开cmd窗口的方式,瞬间把我惊呆了。原来他打开cmd窗口的方式,不是一般的在开始里面输入cmd,然后打开cmd窗口。而是另外一种方式。 我这个同事是个技术控&a…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
