Verilog中的有符号数与无符号数
1. 有符号与无符号最本质的区别在于高位扩展时的扩展规则不同;
对于同一个4‘b1001进行位扩展成8位:
有符号扩展结果为:8’b11111001
无符合扩展结果为: 8'b00001001
2. 同第一点,若在运算中没有涉及位扩展,则有符号与无符号的运算没有啥区别;
例如计算 2’b1001 + 2‘b0010, 在硬件的计算逻辑无论这两个数据是有符号数还是无符号数,还是一个是有符号数,一个是无符号数,硬件上得到的结果都是2’b1011,区别的是后面是用有符号数规则使用这个数据,还是使用无符号数使用该数据;
3. 从人的角度上看,去读取一个有符号和无符号的规则不同;
例如数据4‘b1011,用无符号数规则读取就是11,用有符号读取就是-5;
4. 工具计算的判定逻辑;
1. 有符号数与有符号的运算,结果为有符号数;
1. a[4:0] = signed(4'b1001) + signed(4'b0001) ,则a[5:0] = {1'b1,4'b1010},的有符号数,最高位为符号位扩展;
2. 有符号数与无符号数的运算,结果为无符号数;
1. a[4:0] = signed(4'b1001) + unsigned(4'b0001) ,则a[5:0] = {1'b0,4'b1010}的无符号数,最高位直接扩0;
3. 无符号与无符号的运算,结果为无符号数;
1. a[4:0] = signed(4'b1001) + unsigned(4'b0001) ,则a[5:0] = {1'b0,4'b1010}的无符号数,最高位直接扩0;
4. 运算结果通过$signed 或 $unsigned 指定时,以该指定为准,但等式左边的指定不影响等式右边的运算。
1. unsigned(a[4:0]) = signed(4'b1001) + signed(4'b0001) ,则a[4:0] = {1'b1,4'b1010},的无符号数,最高位为符号位扩展;本来等式右边算出的值{1'b1,4'b1010}赋给无符号数a[5:0];
2. signed(a[4:0]) = signed(4'b1001) + unsigned(4'b0001) ,则a[5:0] = {1'b0,4'b1010}的有符号数。将等式右边的计算结果{1'b0,4'b1010}作为有符号数赋值给a[4:0];
相关文章:

Verilog中的有符号数与无符号数
1. 有符号与无符号最本质的区别在于高位扩展时的扩展规则不同; 对于同一个4‘b1001进行位扩展成8位: 有符号扩展结果为:8’b11111001 无符合扩展结果为: 8b00001001 2. 同第一点,若在运算中没有涉及位扩展,则有符…...

15分钟学 Go 第 47 天 :并发进阶——深入了解Go语言的并发模型!
第47天的学习:并发进阶——深入了解Go语言的并发模型! 目录 Go并发模型简介Goroutines深度讲解Channels的进阶使用Select语句详解并发模型设计模式实战案例分析常见问题与解决方案 1. Go并发模型简介 Go语言以其内置的并发支持而闻名。通过轻量级的g…...

前端代码分析题(选择题、分析题)——this指向、原型链分析
this指向 普通函数:this 的指向由调用方式决定,可以是全局对象、调用该函数的对象,或者显式指定的对象。箭头函数:this 的指向在定义时确定,始终继承自外层函数作用域的 this,不会被调用方式影响。 var obj…...

react 组件应用
文章目录 react 组件react 中组件 hook 函数应用useMemo技术细节(useMemo 钩子函数和 useCallback 钩子函数)小结(依赖性数组应用) react 组件 函数式组件实例及应用场景 实例: 以下是一个简单的函数式组件,用于显示一个欢迎消息。 import React from re…...

mysql 快速解决死锁方式
mysql 快速解决死锁方式 直接寻找并终止导致死锁的具体 SQL 语句是处理死锁的一种有效方法,特别是在高并发环境中。以下步骤和示例展示了如何通过识别、分析和终止长时间运行的 SQL 语句来解决死锁问题。 一、识别那个导致死锁的 SQL 语句 1. 使用 SHOW ENGINE I…...

RabbitMQ 篇-深入了解 RabbitMQ 安装以及 SpringAMQP 的基础使用(声明队列和交换机、发送接收消息、配置 JSON 消息转化器)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 RabbitMQ 初识 1.1 RabbitMQ 安装 2.0 数据隔离 2.1 用户管理 2.2 virtual host 虚拟主机 3.0 SpringAMQP 3.1 RabbitMQ 配置 3.2 发送消息 3.3 接收消息 3.4 Wor…...
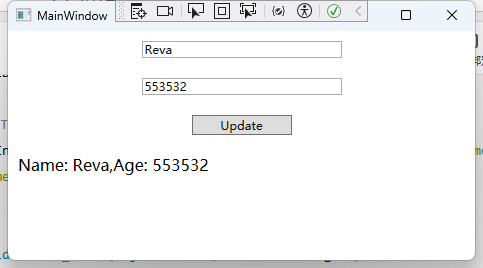
在 WPF 中,绑定机制是如何工作的?WPF数据绑定机制解析
在WPF(Windows Presentation Foundation)中,数据绑定机制是其核心功能之一,广泛用于连接应用程序的UI(用户界面)和应用程序的业务逻辑层。数据绑定允许你将UI元素与数据源(如对象、集合或其他数…...
--Chunk Extend and Overlapping)
pwn学习笔记(12)--Chunk Extend and Overlapping
pwn学习笔记(12)–Chunk Extend and Overlapping chunk extend 是堆漏洞的一种常见利用手法,通过 extend 可以实现 chunk overlapping(块重叠) 的效果。这种利用方法需要以下的时机和条件: 程序中存在…...

java基础面试题六集合框架
目录 1. List,Set,Map是否继承自collection接口? 2. 说说List,Set,Map三者的区别 3. 写出list、map、set接口的实现类,并说出其特点 4. 常见集合类的区别和适用场景 5. 集合的父类是谁?哪些安全的? 6…...

2024年12月一区SCI-指数-三角优化算法ETO-附Matlab免费代码
引言 本期介绍了一种基于数学概念的元启发式优化算法,称为指数-三角优化算法Exponential-trigonometric optimization algorithm,ETO。该算法基于指数函数和三角函数的复杂组合,于2024年12月最新发表在中JCR1区、 中科院1区 SCI期刊Computer…...

设置服务器ssh连接超时时间
在Linux服务器上,您可以通过修改SSH服务器配置文件来设置SSH连接的超时时间。以下是设置SSH连接超时时间的一些步骤: 打开SSH服务器配置文件。这个文件通常是/etc/ssh/sshd_config。sudo nano /etc/ssh/sshd_config在配置文件中,您可以设置以…...
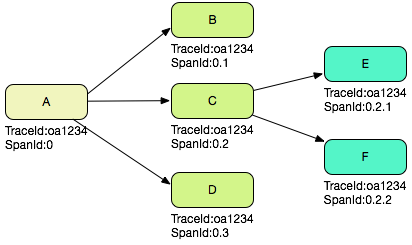
Dubbo分布式日志跟踪实现
前言 随着越来越多的应用逐渐微服务化后,分布式服务之间的RPC调用使得异常排查的难度骤增,最明显的一个问题,就是整个调用链路的日志不在一台机器上,往往定位问题就要花费大量时间。如何在一个分布式网络中把单次请求的整个调用日…...

EPSON机械手与第三方相机的校准功能设计By python
EPSON机械手与第三方相机的校准功能设计By python 使用Python来实现EPSON机械手与第三方相机的校准功能是一个复杂但可行的任务。这通常涉及以下几个步骤:硬件接口通信、图像处理、标定算法实现和控制逻辑编写。 1. 环境准备 首先,库 pip install numpy opencv-python pyse…...

探索 Java 23:新时代的编程利器
一、引言 随着技术的不断发展,Java 作为一种广泛应用的编程语言也在不断演进。Java 23 的推出带来了许多令人兴奋的新特性和改进,为开发者提供了更多的工具和功能,以应对日益复杂的软件开发挑战。本文将深入介绍 Java 23 的各个方面。 二、J…...
)
CSS3_3D变换(七)
1、CSS3_3D变换 1.1 3D空间与景深 3D空间:在父元素中将属性transform-style设置为preserve-3d开启3D空间,默认值为flat(开启2D空间); 景深:人眼与平面的距离,产生透视效果,使得效果…...

Mesh网格
Mesh(网格) 定义:Mesh 是一个包含顶点、三角形、顶点法线、UV坐标、颜色和骨骼权重等数据的对象。它定义了3D模型的几何形状。 功能: 顶点(Vertices):构成3D模型的点。 三角形(Triangles)&…...

LeetCode 509.斐波那契数
动态规划思想 五步骤: 1.确定dp[i]含义 2.递推公式 3.初始化 4.遍历顺序 5.打印dp数组 利用状态压缩,简化空间复杂度。在原代码中,dp 数组保存了所有状态,但实际上斐波那契数列的计算只需要前两个状态。因此,我们…...

SQL Server 数据太多如何优化
大家好,我是 V 哥。讲了很多数据库,有小伙伴说,SQL Server 也讲一讲啊,好吧,V 哥做个听话的门童,今天要聊一聊 SQL Server。 在 SQL Server 中,当数据量增大时,数据库的性能可能会受…...

关于word 页眉页脚的一些小问题
去掉页眉底纹: 对文档的段落边框和底纹进行设置,也是页眉横线怎么删除的一种解决方式,具体操作如下: 选中页眉中的横线文本; 点击【开始】选项卡,在【段落】组中点击【边框】按钮的下拉箭头; …...

【高等数学学习记录】连续函数的运算与初等函数的连续性
一、知识点 (一)连续函数的和、差、积、商的连续性 定理1 设函数 f ( x ) f(x) f(x) 和 g ( x ) g(x) g(x) 在点 x 0 x_0 x0 连续,则它们的和(差) f g f\pm g fg、积 f ⋅ g f\cdot g f⋅g 及商 f g \frac{f…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
