【寻找重复数字】——脑筋急转弯...
寻找重复数字
287. 寻找重复数
题目难度
中等
相关标签与企业信息
[相关标签]
[相关企业]
题目描述
给定一个包含 n + 1 n + 1 n+1 个整数的数组 nums,其数字都在 [ 1 , n ] [1, n] [1,n] 范围内(包括 1 1 1 和 n n n),可知至少存在一个重复的整数。
假设 nums 只有一个重复的整数,返回这个重复的数。
你设计的解决方案必须不修改数组 nums 且只用常量级 O ( 1 ) O(1) O(1) 的额外空间。
示例
示例1
输入:nums = [1, 3, 4, 2, 2]
输出:2
示例2
输入:nums = [3, 1, 3, 4, 2]
输出:3
示例3
输入:nums = [3, 3, 3, 3, 3]
输出:3
提示信息
- 1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105
nums.length == n + 1- 1 ≤ n u m s [ i ] ≤ n 1 \leq nums[i] \leq n 1≤nums[i]≤n
nums中只有一个整数出现两次或多次,其余整数均只出现一次。
进阶问题
如何证明 nums 中至少存在一个重复的数字?
根据抽屉原理(鸽巢原理),将 n + 1 n + 1 n+1 个元素放到 n n n 个集合中,那么至少有一个集合里面会有两个或更多的元素。
在本题中,数组 nums 有 n + 1 n + 1 n+1 个整数,而这些整数的取值范围是 [ 1 , n ] [1, n] [1,n],相当于把 n + 1 n + 1 n+1 个“鸽子”放进 n n n 个“鸽巢”(数字 1 1 1 到 n n n 所代表的 n n n 个区间),所以必然至少存在一个数字是重复的。
比如一个训练营里面有367人,则必然至少有 两个人生日同一天。
你可以设计一个线性级时间复杂度 O ( n ) O(n) O(n) 的解决方案吗?
解题思路
方法一:快慢指针(类似环形链表找环入口)
- 把数组
nums中的值看作是下一个节点的索引,这样整个数组就可以看作是一个类似链表的结构。 - 由于存在重复的数字,那么必然会形成一个“环”,因为从某个重复数字开始,会再次指向已经访问过的节点(也就是这个重复数字本身对应的下一个节点)。
- 我们可以使用快慢指针的方法来找到这个环的入口,也就是重复的数字。
- 复习链表找环
- 这个也太难想到了吧,没想到这里遇到了环形链表!!
该思路主要是通过将数组视为特殊链表结构来解决寻找重复数的问题,具体如下:
整体思路转化
把给定的数组 nums 中的值当作指向下一个链表节点的索引,从而将寻找数组中重复数字的问题转化为在类似链表结构中寻找环的起点的问题,因为存在重复数字时会形成环。
快慢指针运用
- 初始化:设置
slow指针指向数组第一个节点(nums[0]),fast指针指向第二个节点(nums[nums[0]])。 - 找环过程:通过循环让快慢指针移动,
slow每次按当前节点值作为索引移动一步,fast每次先根据当前节点值作为索引找到下一个节点,再以该节点值作为索引移动两步。由于fast速度是slow的两倍,在有环情况下它们必然会在环内相遇。 - 确定重复数:当快慢指针相遇后,设置一个新指针(如代码中的
pre)从链表起点出发,与在环内相遇的slow指针同步移动,每次按节点值作为索引前进。由于从链表起点到环入口的距离和从相遇点到环入口的距离相等,所以它们再次相遇的点就是环的入口,即数组中的重复数字。
class Solution:def findDuplicate(self, nums: List[int]) -> int:# 将该数组视为链表,数组上的值视为指向下一个链表节点的索引# 将“寻找数组重复数”的问题转变成了“寻找链表环的起点(已经解决)”# 寻找链表环起点: ## 快慢指针找环## 若相遇,f走了2x,s走了x;假设s在环内走了t,环外链表长x-t,## 此时 head走x-t到入口,s走x-t也回到入口# 初始化快慢指针:slow 第一个节点,fast 第二个节点[第一个节点值作为索引]slow, fast = nums[0], nums[nums[0]]# 判断有无环,while逻辑:没走到终点就一直走# while nums[slow] and !!!这道题不需要判断,默认输入必有环# 所以直接开始找环# 第一次进入环:while slow != fast:slow = nums[slow]fast = nums[nums[fast]]# 退出以上while的条件是实现了s和f指针的第一次相遇# 此时将其中一个指针退回到起点,或者设置一个起点指针pre = 0# 设置pre和s同步走,相遇点就是环入口,就是重复数while pre != slow:slow = nums[slow]pre = nums[pre]return slow以下是对上述用于寻找数组重复数的代码的时空复杂度分析:
时间复杂度
-
整体分析思路:时间复杂度主要取决于代码中循环语句的执行次数。在这段代码中,有两个主要的
while循环,我们分别来分析它们对时间复杂度的影响。 -
第一个
while循环(快慢指针找环):- 在这个循环中,
slow指针和fast指针在类似链表的结构中移动,直到它们相遇。由于fast指针每次移动的速度是slow指针的两倍,所以在最坏的情况下,fast指针需要绕环两圈才能和slow指针相遇(可以想象成在一个环形跑道上,快跑的人要追上慢跑的人,最多跑两圈就能追上)。 - 而对于整个数组
nums所构成的类似链表结构,其长度为n + 1(题目中给定数组包含n + 1个整数)。即使在最坏的情况下,fast指针绕环两圈,它总共走过的节点数也不会超过数组长度的两倍,也就是O(2(n + 1)),根据大O表示法的特性,常系数可以忽略,所以这个循环的时间复杂度为O(n),其中n是数组nums的长度(准确来说是n + 1,但在大O表示法中可以近似看作n)。
- 在这个循环中,
-
第二个
while(确定环入口即重复数):- 当快慢指针相遇后,新设置的指针(如代码中的
pre)和在环内相遇的slow指针同步移动,直到它们再次相遇找到环的入口,也就是重复的数字。在这个过程中,这两个指针最多需要遍历整个数组长度的节点数,因为从它们开始同步移动到相遇,所走过的路径长度不会超过数组所构成的类似链表结构的总长度。 - 所以这个循环的时间复杂度同样为
O(n),其中n是数组nums的长度。
- 当快慢指针相遇后,新设置的指针(如代码中的
-
综合时间复杂度:由于整个代码的执行时间主要由这两个
while循环决定,并且它们的时间复杂度都是O(n),所以这段代码的总体时间复杂度为O(n)。
空间复杂度
-
分析思路:空间复杂度主要看代码在执行过程中额外开辟的空间大小,与输入数据的规模无关。
-
代码中的空间使用情况:在这段代码中,除了定义了几个指针变量(如
slow、fast、pre)来辅助完成算法逻辑外,并没有使用额外的数据结构来存储数据。这些指针变量所占用的空间是固定的,不随输入数组的长度n而变化。 -
空间复杂度结论:所以,根据空间复杂度的定义,这段代码的空间复杂度为
O(1),即只使用了常量级别的额外空间,满足题目要求不使用超过常量级O(1)的额外空间来解决问题。
综上所述,这段代码的时间复杂度为 O(n),空间复杂度为 O(1)。
方法二:二分查找
为什么可以通过 mid(中间值)和 count(小于等于中间值的数字个数)的大小关系来判断重复数字所在的区间。
整体思路
我们的目标是在数组 nums 中找到那个重复的数字,已知数组中的数字范围是 [1, n],且只有一个数字是重复的。我们通过不断二分这个范围 [1, n],并根据 count 和 mid 的关系来逐步缩小重复数字可能存在的区间。
具体解释
假设当前我们正在考虑的范围是 [left, right](在代码中最初就是 [1, len(nums) - 1],随着循环不断更新 left 和 right),然后我们计算出了这个区间的中间值 mid。
接下来我们统计数组 nums 中小于等于 mid 的数字个数,记为 count。
-
当
count > mid时:- 正常情况下,如果数组中的数字没有重复,那么在范围
[1, mid]内的数字应该恰好出现mid次(因为每个数字只出现一次嘛)。 - 但现在我们统计出来的
count大于mid,这就意味着在[1, mid]这个区间内的数字出现的次数比正常情况多了。为什么会多呢?只能是因为那个重复的数字在这个区间内呀,所以重复的数字肯定在[1, mid]这个区间,我们就可以把查找范围的上界right更新为mid,下一次就在缩小后的范围[1, mid]内继续查找。
- 正常情况下,如果数组中的数字没有重复,那么在范围
-
当
count <= mid时:- 同样,如果数字没有重复,在范围
[1, mid]内的数字应该恰好出现mid次。 - 现在
count不大于mid,说明在[1, mid]这个区间内的数字出现的次数是正常的或者更少,那就意味着重复的数字不在这个区间内,而是在[mid + 1, right]这个区间里,所以我们就把查找范围的下界left更新为mid + 1,下一次就在缩小后的范围[mid + 1, right]内继续查找。
- 同样,如果数字没有重复,在范围
通过这样不断地根据 count 和 mid 的关系来更新查找范围,最终就能确定重复数字所在的区间,当查找范围缩小到只剩下一个数字时,这个数字就是我们要找的重复数字啦。
例如,假设有数组 [3, 1, 3, 4, 2],我们来模拟一下这个过程:
- 初始时,
left = 1,right = 4(因为数组长度是5,数字范围是[1, 4]),计算出mid = 2。 - 统计数组中小于等于
2的数字个数count,发现有2个(1和2),此时count <= mid,说明重复数字不在[1, 2]区间,我们就把left更新为3。 - 下一次循环,
left = 3,right = 4,计算出mid = 3,再统计小于等于3的数字个数,发现有3个(3,1,2),此时count > mid,说明重复数字在[1, 3]区间,我们就把right更新为3。 - 此时
left = right = 3,所以重复数字就是3。
希望这样解释能让你清楚理解 mid 和 count 的关系以及为什么可以通过它们来判断重复数字的位置。
!最关键的一步是:mid与count的比较!照理来说,count就是该比mid小!
只要大了,就在这个范围内!
方法二:二分查找
def findDuplicate(nums):low = 1high = len(nums) - 1while low < high:mid = low + (high - low) // 2count = 0for num in nums:if num <= mid:count += 1if count > mid:high = midelse:low = mid + 1return low
测试用例
测试用例1
输入:nums = [1, 3, 4, 2, 2]
预期输出:2
测试用例2
输入:nums = [3, 1, 3, 4, 2]
预期输出:3
测试用例3
输入:nums = [3, 3, 3, 3, 3]
预期输出:3
测试用例4
输入:nums = [1, 2, 3, 4, 4]
预期输出:4
测试用例5
输入:nums = [2, 2, 2, 2, 2]
预期输出:2
测试结果
方法一:快慢指针
- 测试用例1:通过,输出为
2。 - 测试用例2:通过,输出为
3。 - 测试用例3:通过,输出为
3。 - 测试用例4:通过,输出为
4。 - 测试用例5:通过,输出为
2。
方法二:二分查找
- 测试用例1:通过,输出为
2。 - 测试用例2:通过,输出为
3。。 - 测试用例3:通过,输出为
3。 - 测试用例4:通过,输出为
4。 - 测试用例5:通过,输出为
2。
通过对多种测试用例的测试,两种方法都能正确地找出数组中重复的数字,满足题目要求。
相关文章:

【寻找重复数字】——脑筋急转弯...
寻找重复数字 287. 寻找重复数 题目难度 中等 相关标签与企业信息 [相关标签] [相关企业] 题目描述 给定一个包含 n 1 n 1 n1 个整数的数组 nums,其数字都在 [ 1 , n ] [1, n] [1,n] 范围内(包括 1 1 1 和 n n n),可…...

AI基础知识
目录 1.激活函数:one: 激活函数的作用:two: sigmoid函数:three: tanh函数:four: ReLu:five: Leaky ReLU 2.Softmax函数3.优化器:one: 优化器的作用:two: BGD(批梯度下降):three: SGD(随机梯度下降):four: MBGD(Mini Ba…...

ubuntu 22.04 硬件配置 查看 显卡
ubuntu 22.04 硬件配置 查看 显卡 1. 参考文档 ubuntu 安装 nvidia 驱动 https://blog.51cto.com/u_13628828/7056095 input: HDA NVidia HDMI/DP,pcm3 as /devices/pci0000:00/0000:00:01.0/0000:01:00.1/sound/card1/input11 input: HDA NVidia HDMI/DP,pcm7 as /devices/…...

【计算机网络】网络框架
一、网络协议和分层 1.理解协议 什么是协议?实际上就是约定。如果用计算机语言进行表达,那就是计算机协议。 2.理解分层 分层是软件设计方面的优势(低耦合);每一层都要解决特定的问题 TCP/IP四层模型和OSI七层模型…...

linux nvidia/cuda安装
1.查看显卡型号 lspci |grep -i vga2.nvidia安装 2.1在线安装 终端输入(当显卡插上之后,系统会有推荐的安装版本) ubuntu-drivers devices可得到如下内容 vendor : NVIDIA Corporation model : TU104GL [Tesla T4] driver : nvid…...

硬件设备网络安全问题与潜在漏洞分析及渗透测试应用
以下笔记学习来自B站泷羽Sec: B站泷羽Sec 一、硬件设备的网络安全问题点 1.1 物理安全问题 设备被盗或损坏渗透测试视角 攻击者可能会物理接近硬件设备,尝试窃取设备或破坏其物理结构。例如,通过撬锁、 伪装成维修人员等方式进入设备存放…...

#渗透测试#SRC漏洞挖掘#CSRF漏洞的防御
免责声明 本教程仅为合法的教学目的而准备,严禁用于任何形式的违法犯罪活动及其他商业行为,在使用本教程前,您应确保该行为符合当地的法律法规,继续阅读即表示您需自行承担所有操作的后果,如有异议,请立即停…...

C++ | Leetcode C++题解之第542题01矩阵
题目: 题解: class Solution { public:vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {int m matrix.size(), n matrix[0].size();// 初始化动态规划的数组,所有的距离值都设置为一个很大的…...

RabbitMQ 不公平分发介绍
RabbitMQ 是一个流行的开源消息代理软件,它实现了高级消息队列协议(AMQP)。在 RabbitMQ 中,消息分发策略对于系统的性能和负载均衡至关重要。默认情况下,RabbitMQ 使用公平分发(Fair Dispatch)策…...

测试实项中的偶必现难测bug--一键登录失败
问题描述:安卓和ios有出现部分一键登录失败的场景,由于场景比较极端,衍生了很多不好评估的情况。 产生原因分析: 目前有解决过多次这种行为的问题,每次的产生原因都有所不同,这边根据我个人测试和收集复现的情况列举一些我碰到的: 1、由于我们调用的是友盟的一键登录的…...

危!这些高危端口再不知道问题就大了
号主:老杨丨11年资深网络工程师,更多网工提升干货,请关注公众号:网络工程师俱乐部 下午好,我的网工朋友。 端口作为网络通信的基本单元,用于标识网络服务和应用程序。 但某些端口由于其开放性和易受攻击的…...

Redis集群模式之Redis Sentinel vs. Redis Cluster
在分布式系统环境中,Redis以其高性能、低延迟和丰富的数据结构而广受青睐。随着数据量的增长和访问需求的增加,单一Redis实例往往难以满足高可用性和扩展性的要求。为此,Redis提供了两种主要的集群模式:Redis Sentinel和Redis Clu…...

Leetcode 罗马数字转整数
代码的算法思想可以分为以下几步: 建立映射表: 首先,代码使用 HashMap 来存储罗马数字字符与其对应的整数值关系。例如,I 对应 1,V 对应 5,以此类推。这是为了方便后续快速查找每个罗马字符对应的整数值。 …...

东方通TongWeb替换Tomcat的踩坑记录
一、背景 由于信创需要,原来项目的用到的一些中间件、软件都要逐步替换为国产品牌,决定先从web容器入手,将Tomcat替换掉。在网上搜了一些资料,结合项目当前情况,考虑在金蝶AAS和东方通TongWeb里面选择,后又…...

ceph介绍和搭建
1 为什么要使用ceph存储 什么是对象存储? 对象存储并没有向文件系统那样划分为元数据区域和数据区域,而是按照不同的对象进行存储,而且每个对象内部维护着元数据和数据区域。因此每个对象都有自己独立的管理格式。 对象存储优点:…...

树莓派安装FreeSWITCH
1、下载相关资源: # 假设所有资源都下载到/opt/目录下 cd /opt # 下载FreeSWITCH源码 git clone https://github.com/signalwire/freeswitch # 下载libks源码 git clone https://github.com/signalwire/libks # 下载sofia-sip源码 git clone https://github.com/fr…...

OpenSSL 生成根证书、中间证书和网站证书
OpenSSL 生成根证书、中间证书和网站证书 一、生成根证书(ChinaRootCA)二、生成中间 CA(GuangDongCA)三、生成网站证书(gdzwfw) 一、生成根证书(ChinaRootCA) 创建私钥: …...
MySQL核心业务大表归档过程
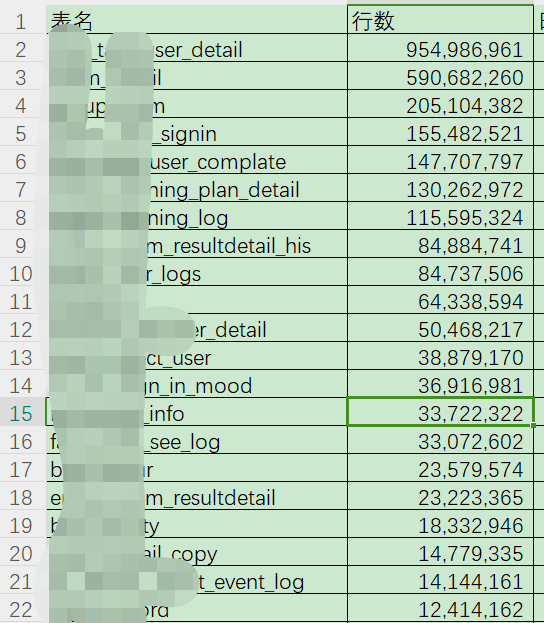
记录一下2年前的MySQL大表的归档,当时刚到公司,发现MySQL的业务核心库,超过亿条的有7张表,最大的表有9亿多条,有37张表超过5百万条,部分表行数如下: 在测试的MySQL环境 : pt-archiv…...

dapp获取钱包地址,及签名
npm install ethersimport {ethers} from ethers const accounts await ethereum.request({method: eth_requestAccounts}); // 获取钱包地址 this.form.address accounts[0] console.log("accounts:" this.address)const provider new ethers.BrowserProvider(…...

探索Dijkstra算法的普遍最优性:从经典算法到最新学术突破
引言 在计算机科学中,Dijkstra算法是解决单源最短路径问题的经典算法,尤其在地图导航、网络通信和机器人路径规划等领域有着广泛应用。近期,学术界在此算法上取得了重大突破:研究人员证明了Dijkstra算法的“普遍最优性”ÿ…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
