背包九讲——背包问题求具体方案
目录
背包问题求具体方案
1. 01 背包问题
题目:12. 背包问题求具体方案 - AcWing题库
算法思路:
代码实现:
2. 多重背包问题
算法思路:
3. 完全背包问题
算法思路:
代码实现:
背包问题第九讲——背包问题求具体方案
背包问题是一类经典的组合优化问题,通常涉及在限定容量的背包中选择物品,以最大化某种价值或利益。问题的一般描述是:有一个背包,其容量为C;有一组物品,每个物品有重量w和价值v。目标是选择一些物品放入背包,使得它们的总重量不超过背包容量,同时总价值最大。
背包问题涉及到了三种基础的背包:01背包、多重背包、完全背包,我们要根据在这几个背包的基础上去计算在获得最大价值的情况下,有几种方案,并输出具体的方案,是求背包问题方案数的进阶版,这个需要打印具体方案了。

背包问题求具体方案
上一篇说了一下背包问题求方案数,下面进行深化一点就是求具体方案了。同上一篇这些问题都是在01背包、多重背包、完全背包基础上演化来的,求具体方案问题会问你一种具体方案(编号序列的字典序最小)或者打印所有具体方案,一般的问题都是问你第一种。若为第二种问法,建议使用C语言的printf进行打印,因为打印所有具体方案,当数据量很大时会有很多输出,使用printf会比cout快一点。根据问题的具体类型,常见的背包问题包括:
1. 01 背包问题
0-1背包问题是指每个物品只有0跟1两种选择即只能选择放或不放,不能分割。给定一组物品,每个物品都有自己的重量和价值,在不超过背包容量的前提下,选择一些物品,使得总价值最大。

题目:12. 背包问题求具体方案 - AcWing题库
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 字典序最小的方案。这里的字典序是指:所选物品的编号所构成的序列。物品的编号范围是 1…N。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一行,包含若干个用空格隔开的整数,表示最优解中所选物品的编号序列,且该编号序列的字典序最小。
物品编号范围是 1…N。
数据范围
0<N,V≤1000
0<vi,wi≤1000输入样例
4 5 1 2 2 4 3 4 4 6输出样例:
1 4
算法思路:
题目要求了输出字典序最小,所以尽量靠前去,尽管有不同的方案所获得最大价值一样,但是要考虑字典序最小,所以一定要选前面的,比如选1,3,5和2,3,4所获得的价值一样,但是要选1,3,5,所以后面遍历下标从小到大遍历的。上面说明了如果第一个物品属于最优解的一种,一定要选它,这样问题就转化成了从2~N寻找最优解问题,以此类推。
状态定义f[i][j]表示从第i个物品开始到最后一个物品背包容量为j所获得的最大价值
状态转移:f[i][j]=max(f[i+1][j],f[i+1][j-v[i]]+w[i])
f[i][j]的上一个状态就是从i+1转移过来的,因为我们定义从第i个物品到最后一个物品,第i+1个物品到最后一个之间的数量是不是比第i个物品到最后一个物品少。f[i+1][j]是不选第i个物品,f[i+1][j-v[i]]+w[i]是选第i个物品。因为我要在所有f[i][j]当中选择一个最大值,所以前面我管不管的先初始化为不选,往后如果背包容量大于体积,那我再看看是选了这个物品总价值是否增大,如果增大就更新,不增大就保持原来。这样写避免了两重判断最优解,会有两个max,这样只有一个max,其实,好好想一想,我前面先初始化为不选,毫无影响的,后面大于体积那我就走if,不大那就不选呗,那不还是初始化为不选。
最后那一段就是查找最优路径了。首先我先初始为背包容量,面对第i个物品时,若背包剩余容量大于体积并且从上一个状态转移过来,选了第i个物品,那它一定是最优解,并且是字典序是最小的,因为我是正序遍历的。
代码实现:
#include<iostream>
using namespace std;
int N,V;
int v[1005],w[1005],f[1005][1005];//f[i][j]表示从第i个物品开始到最后一个物品背包容量为j所获得的最大价值
int main(){cin>>N>>V;for(int i=1;i<=N;i++){cin>>v[i]>>w[i];}for(int i=N;i>=1;i--){//逆序取物,因为f[i][j]定义从i到最后for(int j=0;j<=V;j++){f[i][j]=f[i+1][j];//先初始化为不选第i个物品if(j>=v[i]){//如果背包剩余容量大于物品体积f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);//那就寻找最优解,到底是选还是不选所获得总价值更大}}}int j=V;for(int i=1;i<=N;i++){if(j>=v[i]&&f[i][j]==f[i+1][j-v[i]]+w[i]){//如果f[i][j]从f[i+1][j-v[i]]+w[i]转移过来,那路径就一定是最优路径cout<<i<<" ";j-=v[i];//选了就减去背包容量,方便下次寻找}}return 0;
}2. 多重背包问题
多重背包问题是指每种物品可以取有限次。给定一组物品,每种物品都有自己的重量、价值和一个数量限制,在不超过背包容量的前提下,选择物品的组合使得总价值最大。
算法思路:
多重背包跟01背包解法没有太大的区别,无非就是多重背包需要先进行二进制拆分,把它拆分成01背包再利用01背包求具体方案的模板进行求解。

3. 完全背包问题
完全背包问题是指每种物品可以无限取用,可以理解为无限使用。给定一组物品,每种物品都有一个重量和价值,在不超过背包容量的前提下,选择物品的组合使得总价值最大。
算法思路:
完全背包求具体方案可能就让你写第几种物品选择了几种,例如,第一种物品选择了2个,第二种物品选择了0个...这样无非又是动态规划问题。可以看一下下面思路。
-
定义状态:
- 定义
dp[w]为当背包容量为w时能够取得的最大价值。 - 使用
count[i][w]来记录当背包容量为w时,物品i被选择了多少个。
- 定义
-
状态转移方程:
- 对于每个物品
i,如果它的重量weight[i]小于等于当前背包容量w,则可以选择该物品。 - 状态转移公式为: dp[w]=max(dp[w],dp[w−weight[i]]+value[i])dp[w] = \max(dp[w], dp[w - weight[i]] + value[i])dp[w]=max(dp[w],dp[w−weight[i]]+value[i])
- 在此过程中,需要同时更新
count[i][w]来记录物品的选择次数。
- 对于每个物品
-
初始化:
- 当不选择任何物品时,
dp[0] = 0,其他状态初始化为 0。
- 当不选择任何物品时,
-
最终结果:
dp[W]为在背包容量W时能够取得的最大价值。- 通过
count数组可以得出每种物品的选择次数。
代码实现:
#include <iostream>
#include <vector>
using namespace std;int knapsack(int W, const vector<int>& weight, const vector<int>& value, int n) {vector<int> dp(W + 1, 0);vector<vector<int>> count(n, vector<int>(W + 1, 0));// 动态规划求解完全背包问题for (int i = 0; i < n; ++i) { // 对每个物品进行处理for (int w = weight[i]; w <= W; ++w) { // 每个物品可以被多次选择if (dp[w] < dp[w - weight[i]] + value[i]) {dp[w] = dp[w - weight[i]] + value[i];count[i][w] = count[i][w - weight[i]] + 1; // 记录物品i的选择次数}}}// 输出结果cout << "最大价值: " << dp[W] << endl;cout << "每个物品的选择数量: " << endl;for (int i = 0; i < n; ++i) {cout << "物品 " << i + 1 << ": " << count[i][W] << " 个" << endl;}return dp[W];
}int main() {int W = 10; // 背包容量vector<int> weight = {2, 3, 4}; // 各个物品的重量vector<int> value = {3, 4, 5}; // 各个物品的价值int n = weight.size();knapsack(W, weight, value, n);return 0;
}上一篇博客:背包九讲——背包问题求方案数-CSDN博客
到现在为止,背包九讲问题都更新完了,但是学习不可停止哦,以后我会分享其他的算法,或者再去更新一些知识点和例题,欢迎大家关注。笔者水平有限,一些地方做的不足的地方和需改善的地方大家可以提出来,大家有不明白的地方随时可以私信我,互相学习,大家一起加油!
执笔至此,感触彼多,全文将至,落笔为终,感谢大家支持。
相关文章:

背包九讲——背包问题求具体方案
目录 背包问题求具体方案 1. 01 背包问题 题目:12. 背包问题求具体方案 - AcWing题库 算法思路: 代码实现: 2. 多重背包问题 算法思路: 3. 完全背包问题 算法思路: 代码实现: 背包问题第九讲—…...

Python http打印(http打印body)flask demo(http调试demo、http demo、http printer)
文章目录 代码解释 代码 # flask_http_printer.pyfrom flask import Flask, request, jsonify import jsonapp Flask(__name__)app.route(/printinfo, methods[POST]) def print_info():# 分隔符separator "-" * 60# 获取请求头headers request.headers# 获取 JS…...
)
JSF HTML标签教程一口气讲完!(下)
JSF OutputScript示例 JSF教程 - JSF OutputScript示例 h:outputScript标记渲染类型为“script"的HTML元素,类型为“text/javascript"。 此标记将外部JavaScript文件添加到JSF页面。 以下JSF标记 <h:outputScript library"js" name"…...

cmake报错The link interface of target “gRPC::grpc“ contains: OpenSSL::SSL 解决
系统环境:麒麟V10 报错描述: The link interface of target "gRPC::grpc" contains: OpenSSL::SSL but the target was not found. Possible reasons include: * There is a typo in the target name. * A find_package call is missing fo…...
C语言PythonBash:空白(空格、水平制表符、换行符)与转义字符
C语言 空白 C语言中的空白(空格、水平制表符、换行符)被用于分隔Token,因此Token间可以有任意多个空白。 // 例1 printf("Hello, World!"); 例1中存在5个Token,分别是: printf("Hello, World! \n&qu…...

【Python】轻松解析JSON与XML:Python标准库的json与xml模块
轻松解析JSON与XML:Python标准库的json与xml模块 在现代数据处理与交换中,JSON(JavaScript Object Notation)和XML(eXtensible Markup Language)是最常用的两种数据格式。它们广泛应用于API数据传输、配置…...

物联网对商业领域的影响
互联网彻底改变了通信方式,并跨越了因地理障碍造成的人与人之间的鸿沟。然而,物联网(IoT)的引入通过使设备能够连接到互联网,改变了设备的功能。想象一下,你的闹钟连接到互联网,并且能够用你的声…...

第16章 SELECT 底层执行原理
一、SELECT查询的完整结构 1.1 方式一(SQL 92语法) SELECT ..., ..., ... FROM ..., ..., ... WHERE 多表的连接条件 AND 不包含组函数的过滤条件 GROUP BY ..., ... HAVING 包含组函数的过滤条件 ORDER BY ... ASC/DESC LIMIT ..., ... 1.2 方式二&a…...

python查询日志,并组装sql,修复缺失的数据
前言 由于mysql链接超时波动,导致数据缺失,需要根据日志填补数据 流程 获取确实数据的订单列表 搜索日志,获取请求日志 根据请求日志拼装sql 打印sql供修复数据 代码 因为我们日志打印的有问题,所以这里用字符串截取获取入…...

RecyclerView进阶知识讲解
在 Android 开发中,RecyclerView 是一种高效的列表和网格布局控件,用于显示大规模数据。尽管基本使用方法简单,但深入理解并掌握其高级进阶用法能大幅提升用户体验和应用性能。下面,我将从布局管理、动画和手势、自定义缓存、优化…...

C语言 函数
时间:2024.11.10-11.11 一、学习内容 1、什么是函数 函数:程序中独立的功能。将反复书写的代码,又不确定什么时候回用到的代码打包起来。 2、函数的基本格式 函数的定义格式(写在main函数外) void 函数名() { 函数…...

windows中docker安装redis和redisinsight记录
创建一个Redis运行容器,命令如下 docker run -it -d --name redis -p 6379:6379 redis --bind 0.0.0.0 --protected-mode no -d 代表Redis容器后台运行 --name redis 给创建好的容器起名叫redis -p 6379:6379 将容器的6379端口映射到宿主机的6379端口,注…...

itextpdf打印A5的问题
使用A5打印的时候,再生成pdf是没有问题的。下面做了一个测试,在打印机中,使用A5的纸张横向放入,因为是家用打印机,A5与A4是同一个口,因此只能这么放。 使用itextpdf生成pdf,在浏览器中预览pdf是…...

qt QUndoView详解
1、概述 QUndoView 是 Qt 框架中用于显示 QUndoStack(撤销堆栈)内容的视图类。它通常与 QUndoStack 一起使用,为用户提供了一个可视化的界面来查看和操作撤销/重做历史。QUndoView 可以显示堆栈中的每个命令,并允许用户通过界面进…...

python+智谱AI-实现钉钉消息自动回复
python智谱AI-实现钉钉消息自动回复 实现了电脑窗口切换,截图识别未读消息,与语言模型交互后,将答案带入到钉钉窗口中。偷个懒,直接贴代码了,后续不断完善注释,如果遇到读不懂的地方,欢迎交流。…...

Kafka-Eagle的配置——kafka可视化界面
通过百度网盘分享的文件:kafka-eagle-bin-2.0.8.tar.gz 链接:https://pan.baidu.com/s/1H3YONkL97uXbLTPMZHrfdg?pwdsltu 提取码:sltu 一、界面展示 二、软件配置 1、关闭kafka集群 kf.sh stop 2、将该软件上传到/opt/modules下 cd /opt…...
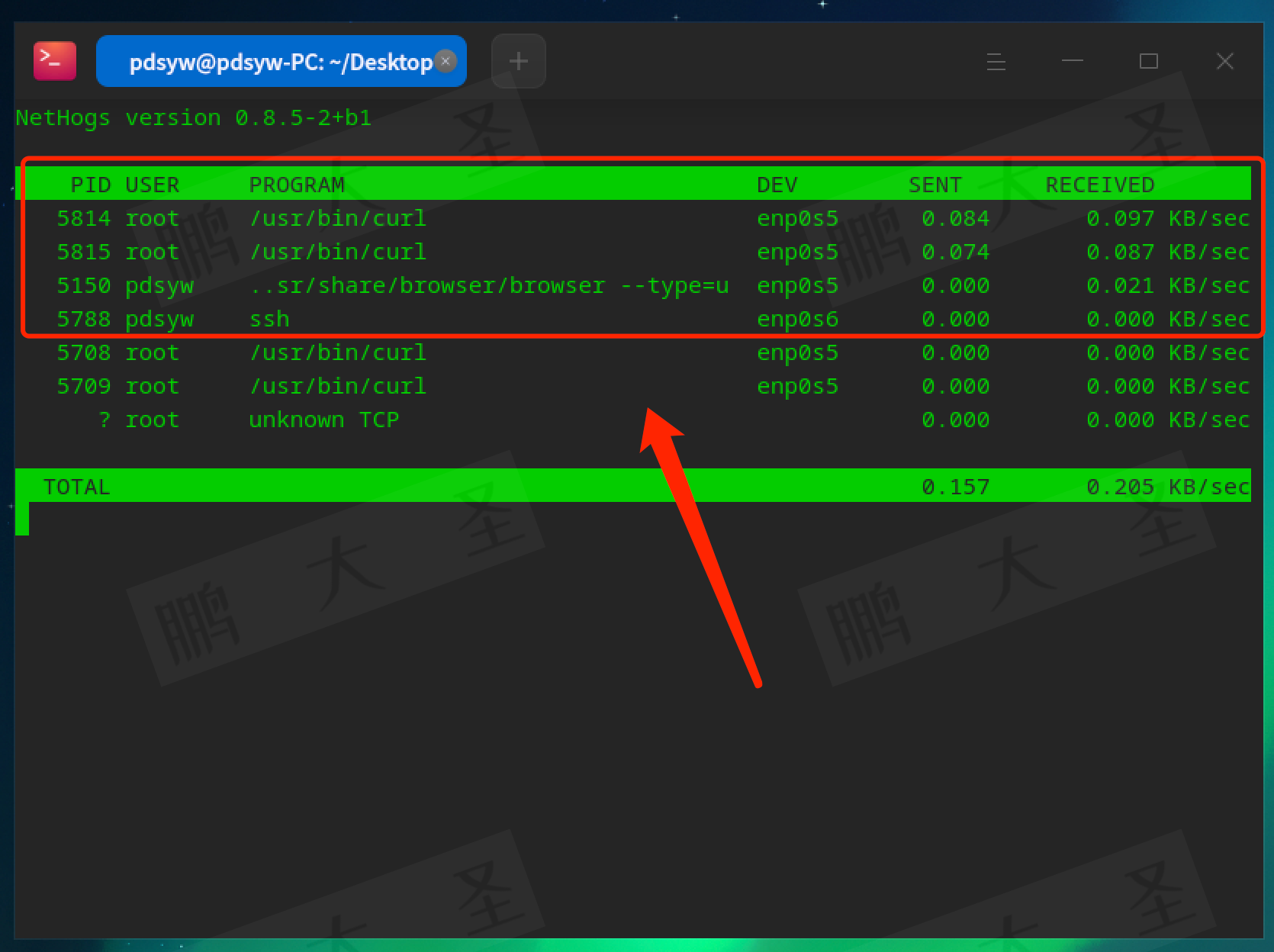
【命令操作】Linux上带宽流量监控nethogs命令详解 _ 统信 _ 麒麟 _ 方德
原文链接:【命令操作】Linux上带宽流量监控nethogs命令详解 | 统信 | 麒麟 | 方德 Hello,大家好啊!今天带来一篇关于Linux上nethogs命令详解的文章。nethogs是一款非常实用的网络流量监控工具,帮助用户实时查看系统中每个进程的网…...

【入门篇】数字统计——多语言版
题目跳转:数字统计 题目解析: 这道题目要求统计在给定范围 [L, R] 内所有整数中数字 2 出现的次数。例如,在范围 [2, 22] 中,数字 2 分别在数 2、12、20、21、22 中出现的次数,最终出现了6次。 题目的输入为两个正…...

探索那些现代C++语法糖
本文来聊聊现代C的一些语法糖。 1.Auto auto x 10; // 推导为 int auto y 3.14; // 推导为 double2.范围-based for 循环 std::vector<int> v {1, 2, 3, 4, 5}; for (auto val : v) {std::cout << val << " "; }3.nullptr int* ptr nullpt…...

【LeetCode】【算法】33. 搜索旋转排序数组
LeetCode 33. 搜索旋转排序数组 题目描述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...
