C 语言标准库 - <errno.h>
目录
1.errno 变量
2.宏
1.errno 变量
errno.h 声明了一个 int 类型的 errno 变量,用来存储错误码(正整数)。
如果这个变量有非零值,表示已经执行的程序发生了错误。
#include <errno.h>
#include <stdio.h>
#include <math.h>
#include <stdlib.h>int main() {int x = -1;errno = 0;int y = sqrt(x);if (errno != 0) {fprintf(stderr, "sqrt error; program terminated.\n");exit(EXIT_FAILURE);}return 0;
}上面示例中,计算一个负值的平方根是不允许的,会导致errno不等于0。
如果要检查某个函数是否发生错误,必须在即将调用该函数之前,将errno的值置为0,防止其他函数改变errno的值。
2.宏
变量errno的值通常是两个宏EDOM或ERANGE。这两个宏都定义在errno.h。它们表示调用数学函数时,可能发生的两种错误。
- 定义域错误(EDOM):传递给函数的一个参数超出了函数的定义域。例如,负数传入
sqrt()作为参数。 - 取值范围错误(ERANGE):函数的返回值太大,无法用返回类型表示。例如,1000 传入
exp()作为参数,因为 e^1000 太大,无法使用 double 类型表示。
使用数学函数时,可以将errno的值与 EDOM 和 ERANGE 比较,用来确定到底发生了哪一类错误。
相关文章:

C 语言标准库 - <errno.h>
目录 1.errno 变量 2.宏 1.errno 变量 errno.h 声明了一个 int 类型的 errno 变量,用来存储错误码(正整数)。 如果这个变量有非零值,表示已经执行的程序发生了错误。 #include <errno.h> #include <stdio.h> #in…...

Golang自带的测试库testing的使用
testing是golang自带的测试库。 testting规则: 在待测试功能所在文件的同级目录中创建一个以_test.go结尾的文件。 测试函数名必须是TestXxxx这个形式,而且Xxxx必须以大写字母开头,另外函数带有一个*testing.T类型的参数。 // 单元测试&am…...

29.电影院售票系统(基于springboot和vue的Java项目)
目录 1.系统的受众说明 2 论文背景 2.1 国内研究现状: 2.2 国外研究现状: 2.3 所用技术 3 系统需求分析 3.1 需求分析 3.2 可行性分析 3.2.1技术可行性分析 3.2.2市场可行性分析 3.2.3经济可…...

大学生就业平台微信小程序
随着计算机技术的成熟,互联网的建立,如今,PC平台上有许多关于大学生就业方面的程序,但由于使用时间和地点上的限制,用户在使用上存在着种种不方便,而开发一款大学生就业平台微信小程序,能够有效…...

Redis 缓存击穿
目录 缓存击穿 什么是缓存击穿? 有哪些解决办法? 缓存穿透和缓存击穿有什么区别? 缓存雪崩 什么是缓存雪崩? 有哪些解决办法? 缓存预热如何实现? 缓存雪崩和缓存击穿有什么区别? 如何保…...
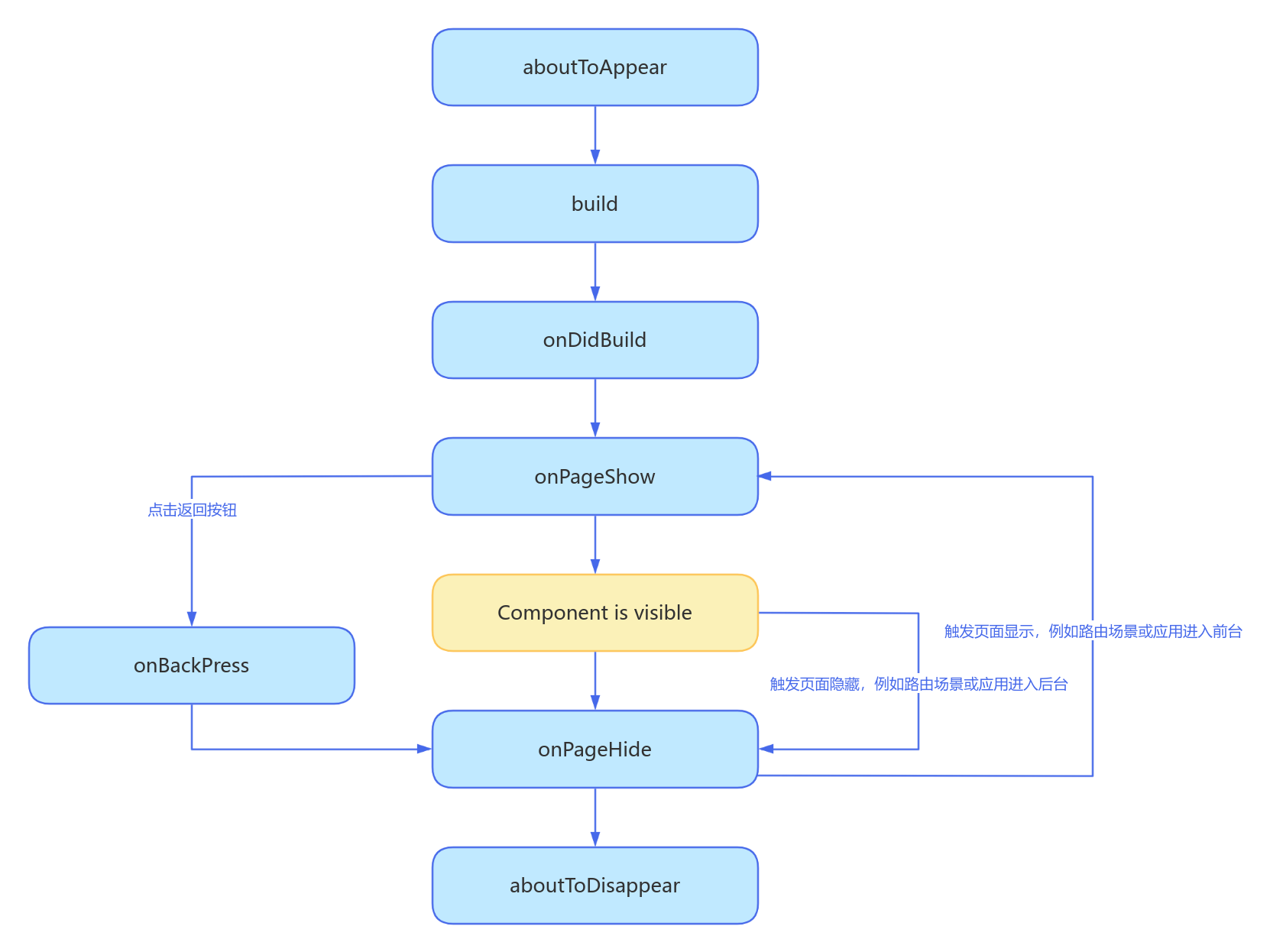
初探鸿蒙:从概念到实践
一、鸿蒙开发的环境准备 开发工具:使用 DevEco Studio,支持 ArkTS 语法。 系统要求:确保计算机符合 DevEco Studio 的最低系统需求。安装步骤:下载 DevEco Studio,安装合适的 SDK 和模拟器 二、鸿蒙应用可以…...

PHP API的路由设计思路
PHP API的路由设计是构建高效、可维护API的关键环节。以下是一套完整的PHP API路由设计思路: 一、明确设计原则 使用统一资源标识符(URI):通过URI来标识资源,确保每个资源都有一个唯一的地址。使用HTTP方法ÿ…...

工程师 - 如何访问Github
Github无法访问,涉及到IP地址、Host文件、DNS等配置。 1,查找github地址 打开https://www.ipaddress.com/网站,这个网站首页是查询自己IP的。 在上方搜索栏输入github.com,查找github的地址。 https://www.ipaddress.com/websit…...

222. 完全二叉树的节点个数 迭代
222. 完全二叉树的节点个数 已解答 简单 相关标签 相关企业 给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值࿰…...

中心极限定理的三种形式
独立同分布的中心极限定理: 设 X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn是独立同分布的随机变量序列,且 E ( X i ) μ E(X_i) \mu E(Xi)μ, D ( X i ) σ 2 > 0 D(X_i) \sigma^2 > 0 D(Xi)σ2>0存在…...

React Native 全栈开发实战班 - 导航栈定制
在 React Native 应用中,导航栈管理是实现页面跳转和状态维护的核心机制。React Navigation 提供了强大的导航栈管理功能,允许开发者灵活地控制页面堆栈、传递参数、处理返回逻辑等。本章节将深入探讨导航栈的管理与定制,包括如何控制导航栈、…...

扬州BGP高防服务器可以给企业带来哪些好处?
扬州BGP服务器是目前江苏较为出名的高防机房,随着网络安全逐渐被企业所重视,扬州机房的也被大家进行选择,但是扬州BGP高防服务器除了可以帮助企业抵御网络攻击,还有着其他的帮助,下面就让我们来了解一下吧!…...

题目讲解15 合并两个排序的链表
原题链接: 合并两个排序的链表_牛客题霸_牛客网 思路分析: 第一步:写一个链表尾插数据的方法。 typedef struct ListNode ListNode;//申请结点 ListNode* BuyNode(int x) {ListNode* node (ListNode*)malloc(sizeof(ListNode));node->…...

leetcode92:反转链表||
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 示例 1: 输入:head [1,2,3,4,5], left 2, right 4 输出:[1,4,3,2…...

arkUI:遍历数据数组动态渲染(forEach)
arkUI:遍历数据数组动态渲染(forEach) 1 主要内容说明2 相关内容2.1 ForEach 的基本语法2.2 简单遍历数组2.2 多维数组遍历2.4 使用唯一键2.5 源码1的相关说明2.5.1 源码1 (遍历数据数组动态渲染)2.5.2 源码1运行效果 …...

js中import引入一个export值可以被修改。vue,react
import引入的数据实际就是数据本身。 如果导出的是一个对象,该对象引入后被更改了,则会影响其他文件引入此对象 解释示例: // resources.js const obj {} export {obj} 当在a.js中import引入一个空对象obj,并且新增一个属性ob…...

PDF24:多功能 PDF 工具使用指南
PDF24:多功能 PDF 工具使用指南 在日常工作和学习中,PDF 是一种常见且重要的文档格式。无论是查看、编辑、合并,还是转换 PDF 文件,能够快速高效地处理 PDF 文档对于提高工作效率至关重要。PDF24 是一款免费、功能全面的 PDF 工具…...

域名解析线路类型有哪几种
在网络世界中,域名解析是将域名转换为IP地址的关键环节,而域名解析线路类型的不同则为域名解析提供了多样化的策略,以满足不同用户和网络环境的需求。以下是几种常见的域名解析线路类型。 电信线路 电信线路解析主要是针对中国电信网络用户…...

Spring资源加载模块,原来XML就这,活该被注解踩在脚下 手写Spring第六篇了
这一篇让我想起来学习 Spring 的时,被 XML 支配的恐惧。明明是写Java,为啥要搞个XML呢?大佬们永远不知道,我认为最难的是 XML 头,但凡 Spring 用 JSON来做配置文件,Java 界都有可能再诞生一个扛把子。 <…...

[运维][Nginx]Nginx学习(2/5)-Nginx高级
Nginx服务器基础配置实例 前面我们已经对Nginx服务器默认配置文件的结构和涉及的基本指令做了详细的阐述。通过这些指令的合理配置,我们就可以让一台Nginx服务器正常工作,并且提供基本的web服务器功能。 接下来我们将通过一个比较完整和最简单的基础配…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
