Leetcode 检测相邻递增子数组
3349. 检测相邻递增子数组 I
给你一个由 n 个整数组成的数组 nums ,请你找出 k 的 最大值,使得存在 两个 相邻 且长度为 k 的 严格递增
子数组
。具体来说,需要检查是否存在从下标 a 和 b (a < b) 开始的 两个 子数组,并满足下述全部条件:
- 这两个子数组
nums[a..a + k - 1]和nums[b..b + k - 1]都是 严格递增 的。 - 这两个子数组必须是 相邻的,即
b = a + k。
返回 k 的 最大可能 值。
子数组 是数组中的一个连续 非空 的元素序列。
示例 1:
输入:nums = [2,5,7,8,9,2,3,4,3,1]
输出:3
解释:
- 从下标 2 开始的子数组是
[7, 8, 9],它是严格递增的。 - 从下标 5 开始的子数组是
[2, 3, 4],它也是严格递增的。 - 这两个子数组是相邻的,因此 3 是满足题目条件的 最大
k值。
示例 2:
输入:nums = [1,2,3,4,4,4,4,5,6,7]
输出:2
解释:
- 从下标 0 开始的子数组是
[1, 2],它是严格递增的。 - 从下标 2 开始的子数组是
[3, 4],它也是严格递增的。 - 这两个子数组是相邻的,因此 2 是满足题目条件的 最大
k值。
提示:
2 <= nums.length <= 2 *-<= nums[i] <=
思路
和下一题 检测相邻递增子数组 II 的思路一样,只需要判断 ans >= k
代码
class Solution {public boolean hasIncreasingSubarrays(List<Integer> nums, int k) {int ans = 0;int preCnt = 0;int cnt = 0;for(int i = 0; i < nums.size(); i++){cnt++;if(i == nums.size()-1 || nums.get(i) >= nums.get(i+1)){ans = Math.max(ans,Math.max(cnt /2, Math.min(preCnt,cnt)));preCnt = cnt;cnt = 0;}}return ans >= k;}
}参考:. - 力扣(LeetCode)
3350. 检测相邻递增子数组 II
给你一个由 n 个整数组成的数组 nums ,请你找出 k 的 最大值,使得存在 两个 相邻 且长度为 k 的 严格递增
子数组
。具体来说,需要检查是否存在从下标 a 和 b (a < b) 开始的 两个 子数组,并满足下述全部条件:
- 这两个子数组
nums[a..a + k - 1]和nums[b..b + k - 1]都是 严格递增 的。 - 这两个子数组必须是 相邻的,即
b = a + k。
返回 k 的 最大可能 值。
子数组 是数组中的一个连续 非空 的元素序列。
示例 1:
输入:nums = [2,5,7,8,9,2,3,4,3,1]
输出:3
解释:
- 从下标 2 开始的子数组是
[7, 8, 9],它是严格递增的。 - 从下标 5 开始的子数组是
[2, 3, 4],它也是严格递增的。 - 这两个子数组是相邻的,因此 3 是满足题目条件的 最大
k值。
示例 2:
输入:nums = [1,2,3,4,4,4,4,5,6,7]
输出:2
解释:
- 从下标 0 开始的子数组是
[1, 2],它是严格递增的。 - 从下标 2 开始的子数组是
[3, 4],它也是严格递增的。 - 这两个子数组是相邻的,因此 2 是满足题目条件的 最大
k值。
提示:
2 <= nums.length <= 2 *-<= nums[i] <=
思路
最后的结果有两个选择,一是只有一个连续的子数组,子数组长度为 n,那么 k = n / 2。二是 有两个连续的子数组(就算有多个连续的子数组,每次也只看两个,只要最后覆盖了这多个连续的子数组即可),长度分别为 preCnt 和 cnt,那么此时 k = Math.min( preCnt, cnt)
代码
具体实现上有两个注意点,一是更新结果的时机:当遍历到末尾或者 nums.get(i) >= nums.get(i+1) 时,更新结果。二是更新结果时要注意 取 ans 与 Math.max(cnt/2, Math.min(cnt, preCnt )) 之间的较大值,保证最后可以返回最大的结果。
class Solution {public int maxIncreasingSubarrays(List<Integer> nums) {int ans = 0;int preCnt = 0;int cnt = 0;for (int i = 0; i < nums.size(); i++) {cnt++;if (i == nums.size() - 1 || nums.get(i) >= nums.get(i + 1)) {ans = Math.max(ans, Math.max(cnt / 2, Math.min(cnt, preCnt)));preCnt = cnt;cnt = 0;}}return ans;}
}参考:. - 力扣(LeetCode)
相关文章:
Leetcode 检测相邻递增子数组
3349. 检测相邻递增子数组 I 给你一个由 n 个整数组成的数组 nums ,请你找出 k 的 最大值,使得存在 两个 相邻 且长度为 k 的 严格递增 子数组 。具体来说,需要检查是否存在从下标 a 和 b (a < b) 开始的 两个 子数组,并满…...

rockylinux 8安装 gcc11.2
方法 1:从源代码编译安装最新版本的 GCC 下载 GCC 源代码: 访问 GCC 官方网站下载最新版本的源代码,例如: wget https://ftp.gnu.org/gnu/gcc/gcc-11.2.0/gcc-11.2.0.tar.gz tar -xf gcc-11.2.0.tar.gz cd gcc-11.2.0安装依赖项&a…...
-奇数序列排序)
【蓝桥等考C++真题】蓝桥杯等级考试C++组第13级L13真题原题(含答案)-奇数序列排序
C L13 奇数序列排序 给定一个长度为N的正整数序列, 请将其中的所有奇数取出,并按增序(从小到大)输出。 输入: 共2行 第1行是一个正整数 N(不大于500); 第2行有 N 个正整数&#x…...

【AI】好用的AI记录
好用的AI 一、国内 KIMI通义 二、国外 GPT4Cursorv0...

linux安装boost.python
前言 boost.python库被用于C与Python代码间的交互,提供了两者间大部分数据类型的转换 相关环境 操作系统:Ubuntu 20.04 python版本:Python 3.8 boost版本:boost 1.78.0 安装 1.boost.python检查与卸载 在安装boost之前需要检…...

AI 扩展开发者思维方式:以 SQL 查询优化为例
在现代软件开发中,AI 技术的兴起让开发者的思维方式发生了显著变化。尤其是在 SQL 查询优化、代码重构以及算法设计等领域,AI 提供的建议不仅扩展了开发者的思考路径,还帮助他们发现以往没有意识到的潜在解决方案。 1. 传统思维模式下的 SQL…...
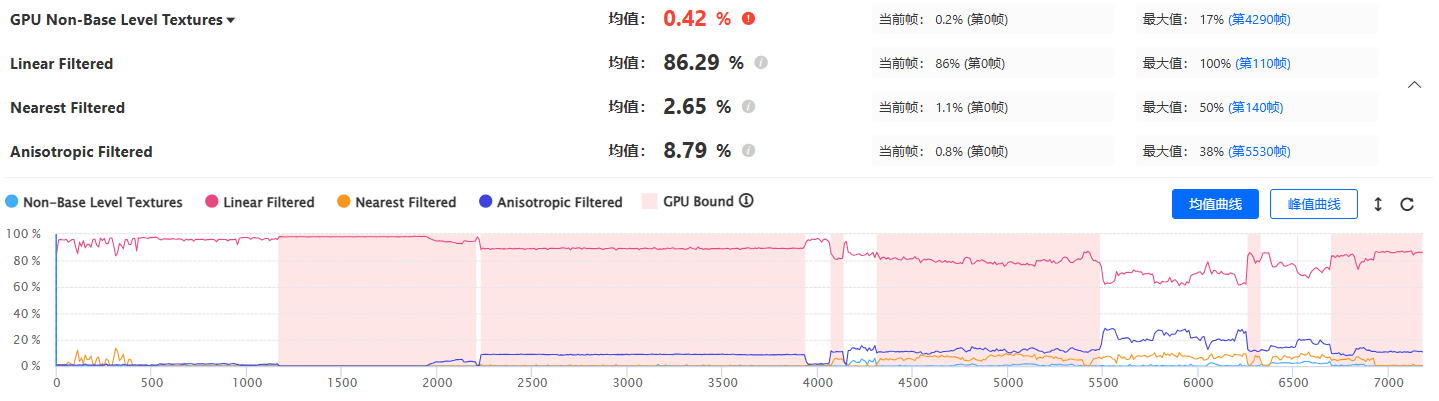
自定义面板,高效的游戏性能分析利器
为了更有效地聚焦并解决性能问题,UWA报告采用了分模块监控策略,确保每个模块独立成章,各司其职。然而,随着对性能分析需求的不断升级,我们已经意识到,在深入分析某些跨模块的性能瓶颈或优化点时,…...

【Linux进程特别篇】深度理解辨识僵尸进程和孤儿进程
--------------------------------------------------------------------------------------------------------------------------------- 每日鸡汤:每一份坚持都是成功的积累,只要相信自己,总会遇到惊喜。 -----------------------------…...

喜报|超维机器人荣获昇腾AI创新大赛铜奖
近日,在备受瞩目的昇腾AI创新大赛中,超维机器人凭借扎实的技术实力和创新产品,荣获大赛铜奖。这一荣誉不仅展现了超维机器人在智能巡检领域的技术创新与突破,也标志着超维机器人的智能巡检解决方案在人工智能领域获得了广泛认可&a…...

从五种架构风格推导出HTTP的REST架构
在分布式系统中,架构风格(Architectural Style)决定了系统组件如何交互、通信、存储和管理数据。每种架构风格都有其独特的特性和适用场景。本文将从五种典型的架构风格出发,逐步探讨它们如何影响了REST(Representational State Transfer,表述性状态转移)架构风格的设计…...

vue-h5:在h5中实现相机拍照加上身份证人相框和国徽框
方案1:排出来照片太糊了,效果不好 1.基础功能 参考: https://blog.csdn.net/weixin_45148022/article/details/135696629 https://juejin.cn/post/7327353533618978842?searchId20241101133433B2BB37A081FD6A02DA60 https://www.freesio…...

免费HTML模板和CSS样式网站汇总
HTML模板:(注意版权,部分不可商用) 1、Tooplate,免费HTML模板下载 Download 60 Free HTML Templates for your websitesDownload 60 free HTML website templates or responsive Bootstrap templates instantly from T…...
备份特殊文件)
Mac打开time machine(时间机器)备份特殊文件
Mac 打开time machine(时间机器)备份特殊文件 设置“时间机器”的作用具体操作办法 前言:今天在使用Nas同步文件时发现有部分重要文件没有同步,为了省事手动拖拽复制文件,导致其中一份非常重要的文件丢失,尝…...

Qt 学习第十六天:文件和事件
一、创建widget对象(文件) 二、设计ui界面 放一个label标签上去,设置成box就可以显示边框了 三、新建Mylabel类 四、提升ui界面的label标签为Mylabel 五、修改mylabel.h,mylabel.cpp #ifndef MYLABEL_H #define MYLABEL_H#incl…...

nvm 切换 Node.js 版本
nvm 切换 Node.js 版本 0. nvm 安装1. 查看装了哪些 Node.js 版本2. 安装 Node.js 版本安装最新稳定版本.安装个18 3. 切换 Node.js 版本4. 设置默认 Node.js 版本5. 卸载 Node.js 版本6.与项目的配合使用参考资料 0. nvm 安装 安装教程就不写了,直接看别人的。 脚…...

AI绘图最强软件stable diffusion,一文带你迅速了解!
有需要stable diffusion整合包可以扫描下方,免费获取 01 — 什么是 SD Stable Difusion(简称 SD) 其三种概念。 1.用来指代稳定扩散(Stable Diffusion) 技术,如 Midjourney是基于Stable Difusion技术实现的就是指它运用了 Stable Diffusion 的技术原理。 …...

VMware重磅官宣!Workstation和Fusion彻底全部免费:支持商用
VMware 官网宣布:VMware Workstation Pro: Now Available Free for Personal Use 别问,问就是正版用户!!! VMware宣布,其桌面虚拟化产品VMware Workstation和VMware Fusion将对所有用户彻底免费࿰…...

CCS 学习记录
1.导入项目 在CCS菜单中选择Project->Import Existing CCS Eclipse Project,点击Browse找到CCS workspace所在文件夹,点击OK,CCS会自动将所选文件夹及其子文件夹下所有的CCS Projects列出。从列表中找到所要导入的项目文件夹,…...

241112.学习日志——[CSDIY] Cpp零基础速成 [01]
CSDIY:这是一个非科班学生的努力之路,从今天开始这个系列会长期更新,(最好做到日更),我会慢慢把自己目前对CS的努力逐一上传,帮助那些和我一样有着梦想的玩家取得胜利!!&…...

94.【C语言】数据结构之双向链表的初始化,尾插,打印和尾删
目录 1.双向链表 2.结构体的定义 3.示意图 3.代码示例 1.双向链表的尾插 示意图 代码 main.c List.h List.c 详细分析代码的执行过程 双向链表的初始化 2.双向链表的打印 代码 3.双向链表的尾删 1.双向链表 以一种典型的双向链表为例:带头双向循环链表(带头:带…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
