LeetCode 3242.设计相邻元素求和服务:哈希表
【LetMeFly】3242.设计相邻元素求和服务:哈希表
力扣题目链接:https://leetcode.cn/problems/design-neighbor-sum-service/
给你一个 n x n 的二维数组 grid,它包含范围 [0, n2 - 1] 内的不重复元素。
实现 neighborSum 类:
neighborSum(int [][]grid)初始化对象。int adjacentSum(int value)返回在grid中与value相邻的元素之和,相邻指的是与value在上、左、右或下的元素。int diagonalSum(int value)返回在grid中与value对角线相邻的元素之和,对角线相邻指的是与value在左上、右上、左下或右下的元素。

示例 1:
输入:
["neighborSum", "adjacentSum", "adjacentSum", "diagonalSum", "diagonalSum"]
[[[[0, 1, 2], [3, 4, 5], [6, 7, 8]]], [1], [4], [4], [8]]
输出: [null, 6, 16, 16, 4]
解释:

- 1 的相邻元素是 0、2 和 4。
- 4 的相邻元素是 1、3、5 和 7。
- 4 的对角线相邻元素是 0、2、6 和 8。
- 8 的对角线相邻元素是 4。
示例 2:
输入:
["neighborSum", "adjacentSum", "diagonalSum"]
[[[[1, 2, 0, 3], [4, 7, 15, 6], [8, 9, 10, 11], [12, 13, 14, 5]]], [15], [9]]
输出: [null, 23, 45]
解释:

- 15 的相邻元素是 0、10、7 和 6。
- 9 的对角线相邻元素是 4、12、14 和 15。
提示:
3 <= n == grid.length == grid[0].length <= 100 <= grid[i][j] <= n2 - 1- 所有
grid[i][j]值均不重复。 adjacentSum和diagonalSum中的value均在范围[0, n2 - 1]内。- 最多会调用
adjacentSum和diagonalSum总共2 * n2次。
解题方法:哈希表
使用哈希表记录每个值的adjacentSum和diagonalSum,查询操作的时候直接去哈希表里查询就可以了。
- 时间复杂度:初始化 O ( n 2 ) O(n^2) O(n2)单次查询 O ( 1 ) O(1) O(1)
- 空间复杂度:初始化 O ( n 2 ) O(n^2) O(n2)单次查询 O ( 1 ) O(1) O(1)
AC代码
C++
const int adj[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
const int dia[4][2] = {{-1, -1}, {-1, 1}, {1, -1}, {1, 1}};class NeighborSum {
private:vector<pair<int, int>> cache;
public:NeighborSum(vector<vector<int>>& grid) {int n = grid.size();cache.resize(n * n);for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {int cntAdj = 0, cntDia = 0;for (int k = 0; k < 4; k++) {int x = i + adj[k][0], y = j + adj[k][1];if (x >= 0 && x < n && y >= 0 && y < n) {cntAdj += grid[x][y];}x = i + dia[k][0], y = j + dia[k][1];if (x >= 0 && x < n && y >= 0 && y < n) {cntDia += grid[x][y];}}cache[grid[i][j]] = {cntAdj, cntDia};}}}int adjacentSum(int value) {return cache[value].first;}int diagonalSum(int value) {return cache[value].second;}
};
Python
from typing import Listdirection = [[-1, 0], [1, 0], [0, -1], [0, 1], [-1, -1], [1, 1], [-1, 1], [1, -1]]class NeighborSum:def __init__(self, grid: List[List[int]]):n = len(grid)self.cache = [[0, 0] for _ in range(n * n)]for i in range(n):for j in range(n):for th, (x, y) in enumerate(direction):if 0 <= x + i < n and 0 <= y + j < n:self.cache[grid[i][j]][th // 4] += grid[x + i][y + j]def adjacentSum(self, value: int) -> int:return self.cache[value][0]def diagonalSum(self, value: int) -> int:return self.cache[value][1]
Java
class NeighborSum {private static final int[][] direction = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}, {-1, -1}, {-1, 1}, {1, -1}, {1, 1}};private int[][] cache;public NeighborSum(int[][] grid) {int n = grid.length;cache = new int[n * n][2];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {for (int k = 0; k < 8; k++) {int x = i + direction[k][0], y = j + direction[k][1];if (x >= 0 && x < n && y >= 0 && y < n) {cache[grid[i][j]][k / 4] += grid[x][y];}}}}}public int adjacentSum(int value) {return cache[value][0];}public int diagonalSum(int value) {return cache[value][1];}
}
Go
package mainvar direction = []struct{x, y int}{{-1, 0}, {1, 0}, {0, -1}, {0, 1}, {-1, -1}, {-1, 1}, {1, -1}, {1, 1}}
type Value [][2]inttype NeighborSum struct {cache Value
}func Constructor(grid [][]int) NeighborSum {n := len(grid)var neighborSum NeighborSumneighborSum.cache = make(Value, n * n)for i, row := range grid {for j, v := range row {for k, d := range direction {x, y := i + d.x, j + d.yif x >= 0 && x < n && y >= 0 && y < n {neighborSum.cache[v][k / 4] += grid[x][y]}}}}return neighborSum
}func (this *NeighborSum) AdjacentSum(value int) int {return this.cache[value][0]
}func (this *NeighborSum) DiagonalSum(value int) int {return this.cache[value][1]
}
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/143698347
相关文章:

LeetCode 3242.设计相邻元素求和服务:哈希表
【LetMeFly】3242.设计相邻元素求和服务:哈希表 力扣题目链接:https://leetcode.cn/problems/design-neighbor-sum-service/ 给你一个 n x n 的二维数组 grid,它包含范围 [0, n2 - 1] 内的不重复元素。 实现 neighborSum 类: …...

【AliCloud】ack + ack-secret-manager + kms 敏感数据安全存储
介绍 ack-secret-manager支持以Kubernetes Secret实例的形式向集群导入或同步KMS凭据信息,确保您集群内的应用能够安全地访问敏感信息。通过该组件,您可以实现密钥数据的自动更新,使应用负载通过文件系统挂载指定Secret实例来使用凭据信息&a…...

探索JavaScript的强大功能:从基础到高级应用
随着互联网技术的不断发展,JavaScript已经成为现代Web开发的基石。无论是简单的交互效果,还是复杂的前端框架,JavaScript都在其中扮演着不可或缺的角色。本文旨在对JavaScript进行深入探讨,从其基础概念到高级应用,并讨…...

新增支持Elasticsearch数据源,支持自定义在线地图风格,DataEase开源BI工具v2.10.2 LTS发布
2024年11月11日,人人可用的开源BI工具DataEase正式发布v2.10.2 LTS版本。 这一版本的功能变动包括:数据源方面,新增了对Elasticsearch数据源的支持;图表方面,对地图类和表格类图表进行了功能增强和优化,增…...

Spark的容错机制
1,Spark如何保障数据的安全 1、RDD容错机制:persist持久化机制 1)cache算子 - 功能:将RDD缓存在内存中 - 语法:cache() - 本质:底层调用的还是persist(StorageLevel.MEMORY_ONLY)&…...

YOLOv8改进 | 利用YOLOv8进行视频划定区域目标统计计数
简介 本项目旨在利用YOLOv8算法来实现视频中划定区域目标的统计计数。YOLOv8是一种目标检测算法,能够实现实时目标检测和定位。视频划定区域目标统计计数是指在一个视频中,对于指定的区域,统计出该区域内出现的目标物体数量。 该项目的工作流程如下:首先,利用YOLOv8算法…...

基于yolov8、yolov5的番茄成熟度检测识别系统(含UI界面、训练好的模型、Python代码、数据集)
摘要:番茄成熟度检测在农业生产及质量控制中起着至关重要的作用,不仅能帮助农民及时采摘成熟的番茄,还为自动化农业监测提供了可靠的数据支撑。本文介绍了一款基于YOLOv8、YOLOv5等深度学习框架的番茄成熟度检测模型,该模型使用了…...

wafw00f源码详细解析
声明 本人菜鸟一枚,为了完成作业,发现网上所有的关于wafw00f的源码解析都是这抄那那抄这的,没有新东西,所以这里给出一个详细的源码解析,可能有错误,如果有大佬发现错误,可以在评论区平和的指出…...

什么是crm?3000字详细解析
在现代商业环境中,客户关系管理(CRM)已经成为企业驱动成功的关键工具。在复杂且竞争激烈的市场中,如何有效地管理客户关系、提升客户满意度,并增加客户忠诚度,越来越成为企业迫切关心的问题。而CRM系统&…...

WEB3.0介绍
Web3.0是对Web2.0的改进,被视为互联网潜在的下一阶段。 以下是对Web3.0的详细介绍: 一、定义与概念 Web3.0被描述为一个运行在区块链技术之上的去中心化互联网。它旨在构建一个更加自主、智能和开放的互联网环境,其中用户不必 在不同中心化…...

【深度学习】LSTM、BiLSTM详解
文章目录 1. LSTM简介:2. LSTM结构图:3. 单层LSTM详解4. 双层LSTM详解5. BiLSTM6. Pytorch实现LSTM示例7. nn.LSTM参数详解 1. LSTM简介: LSTM是一种循环神经网络,它可以处理和预测时间序列中间隔和延迟相对较长的重要事件。LSTM通…...

分子对接--软件安装
分子对接相关软件安装 一、软件 AutoDock,下载链接: linkMGLtools,下载链接: link 自行选择合适版本下载,这里主要叙述在win上的具体安装流程: 下载得到: 二、运行 运行autodocksuite-4.2.6.i86Windows得到&#…...

【Python无敌】在 QGIS 中使用 Python
QGIS 中有 Python 的运行环境,可以很好地执行各种任务。 这里的问题是如何在 Jupyter 中调用 QGIS 的功能。 首先可以肯定的是涉及到 GUI 的一些任务是无法在 Jupyter 中访问的, 这样可以用的功能主要是地处理工具。 按如下方式进行了尝试。 原想使用 gdal:hillshade ,但是…...

全面解读:低代码开发平台的必备要素——系统策划篇
在传统开发过程中,系统策划起着举足轻重的作用,它宛如一位幕后的总指挥,把控着整个软件开发项目的走向。而随着技术的不断进步,低代码开发平台逐渐崭露头角,它以快速开发、降低技术门槛等优势吸引了众多企业和开发者的…...

Vue开发自动生成验证码功能 前端实现不使用第三方插件实现随机验证码功能,生成的验证码添加干扰因素
Vue实现不使用第三方插件,开发随机生成验证码功能 效果图,其中包含了短信验证码功能,以及验证码输入是否正确功能 dom结构 <div class="VerityInputTu"><div class="labelClass">图形验证码</div><div class="tuxingInput…...

# filezilla连接 虚拟机ubuntu系统出错“尝试连接 ECONNREFUSED - 连接被服务器拒绝, 失败,无法连接服务器”解决方案
filezilla连接 虚拟机ubuntu系统出错“尝试连接 ECONNREFUSED - 连接被服务器拒绝, 失败,无法连接服务器”解决方案 一、问题描述: 当我们用filezilla客户端 连接 虚拟机ubuntu系统时,报错“尝试连接 ECONNREFUSED - 连接被服务…...

2024/11/13 英语每日一段
The new policy has drawn many critics. Data and privacy experts said the Metropolitan Transit Authority’s new initiative doesn’t address the underlying problem that causes fare evasion, which is related to poverty and access. Instead, the program tries “…...

【全栈开发平台】全面解析 StackBlitz 最新力作 Bolt.new:AI 驱动的全栈开发平台
文章目录 [TOC]🌟 Bolt.new 的独特价值1. **无需配置,立刻开发**2. **AI 驱动,智能生成代码**3. **极致的速度与安全性**4. **一键部署,轻松上线**5. **免费开放,生态丰富** 🛠️ Bolt.new 使用教程一、快速…...
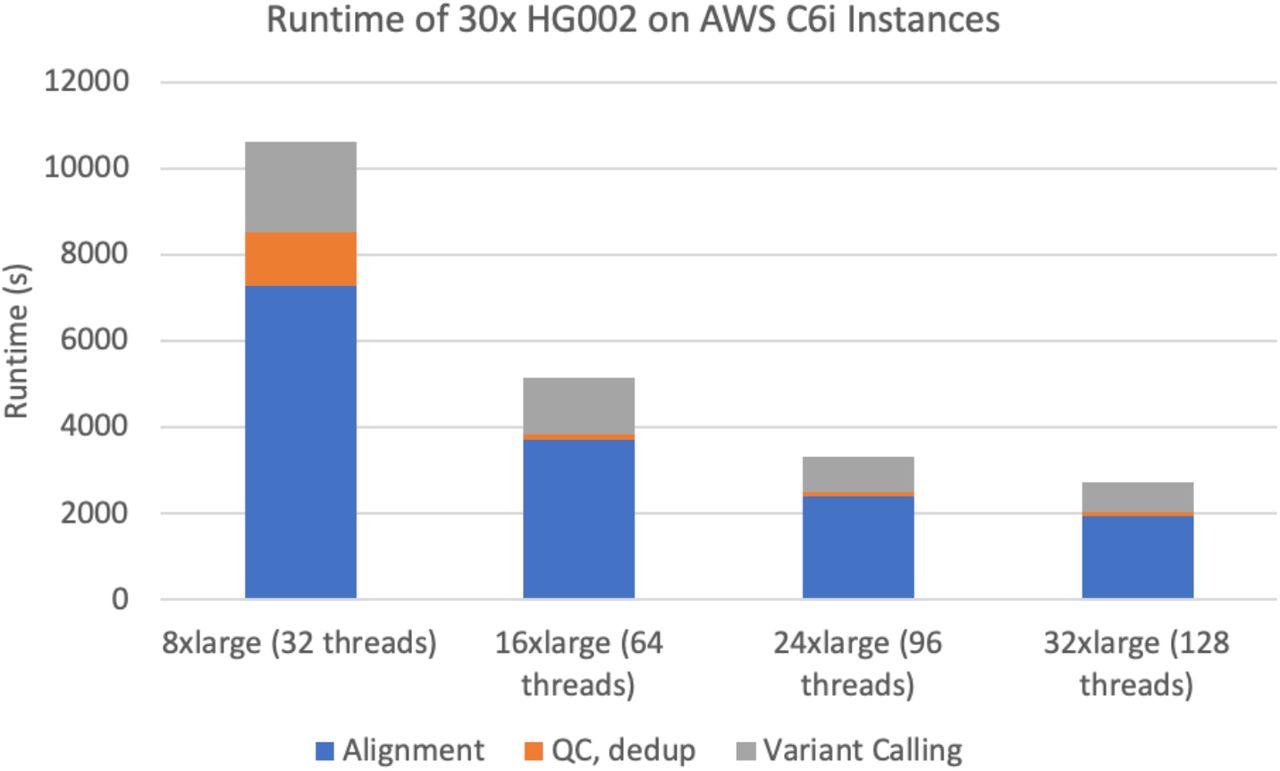
文献解读-DNAscope: High accuracy small variant calling using machine learning
关键词:基准与方法研究;基因测序;变异检测; 文献简介 标题(英文):DNAscope: High accuracy small variant calling using machine learning标题(中文):DNAsc…...

成都睿明智科技有限公司解锁抖音电商新玩法
在这个短视频风起云涌的时代,抖音电商以其独特的魅力迅速崛起,成为众多商家争夺的流量高地。而在这片充满机遇与挑战的蓝海中,成都睿明智科技有限公司犹如一颗璀璨的新星,以其专业的抖音电商服务,助力无数品牌实现从零…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
