day60 图论章节刷题Part10(Floyd 算法、A * 算法)
Floyd 算法
思路:本题是多源最短路问题,使用Floyd算法求解。Floyd 算法对边的权值正负没有要求,核心思想是动态规划。
我们使用动规五部曲来理解和应用Floyd算法:
1、确定dp数组(dp table)以及下标的含义
我们用 grid数组来存图,那就把dp数组命名为 grid。grid[i][j][k] = m,表示 节点i 到 节点j 以[1…k] 集合为中间节点的最短距离为m。
2、确定递推公式
分两种情况:
(1)节点i 到 节点j 的最短路径经过节点k:grid[i][j][k] = grid[i][k][k - 1] + grid[k][j][k - 1]
(2)节点i 到 节点j 的最短路径不经过节点k:grid[i][j][k] = grid[i][j][k - 1]
因为求最短路,取两种情况的最小值: grid[i][j][k] = min(grid[i][k][k - 1] + grid[k][j][k - 1], grid[i][j][k - 1])
3、dp数组初始化
在开始输入边时不经过其他节点,可以把k 赋值为 0,即grid[i][j][0]。同时,本题求的是最小值,grid数组中其他元素数值应该初始为一个最大数。
4、确定遍历顺序
从递推公式:grid[i][j][k] = min(grid[i][k][k - 1] + grid[k][j][k - 1], grid[i][j][k - 1]) 可以看出,我们需要三个for循环,分别遍历i,j 和k。我们把 k =0 的 i 和j 对应的数值都初始化了,再去计算 k = 1 时 i 和 j 对应的数值。这就好比是一个三维坐标,i 和j 是平层,而k 是 垂直向上 的。遍历的顺序是从底向上 一层一层去遍历。所以遍历k 的for循环一定是在最外面。
5、举例推导dp数组
代码如下:
import java.util.*;
public class Main{public static void main (String[] args) {Scanner scan =new Scanner(System.in);int n=scan.nextInt();int m=scan.nextInt();int[][][] grid=new int[n+1][n+1][n+1];for(int i=0;i<=n;i++){for(int j=0;j<=n;j++){Arrays.fill(grid[i][j],Integer.MAX_VALUE);}}//添加边的权重,初始化for(int i=0;i<m;i++){int l=scan.nextInt();int r=scan.nextInt();int val=scan.nextInt();grid[l][r][0]=val;grid[r][l][0]=val;}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if (grid[i][k][k - 1] != Integer.MAX_VALUE && grid[k][j][k - 1] != Integer.MAX_VALUE) {grid[i][j][k] = Math.min(grid[i][k][k - 1] + grid[k][j][k - 1], grid[i][j][k - 1]);} else {grid[i][j][k] = grid[i][j][k - 1];}}}}int num=scan.nextInt();while(num>0){int start=scan.nextInt();int end=scan.nextInt();num--;if(grid[start][end][n]==Integer.MAX_VALUE) System.out.println(-1);else System.out.println(grid[start][end][n]);}}
}
注意:当两个 Integer.MAX_VALUE 值相加时,会导致整数溢出,结果会变成一个非常小的负数,如 -128。
A * 算法(A star算法)
Astar 是一种 广搜或者 dijkstra 的改良版。在搜索最短路的时候, 如果是无权图(边的权值都是1) 那就用广搜,代码简洁,时间效率和 dijkstra 差不多;如果是有权图(边有不同的权值),优先考虑 dijkstra。
Astar 关键在于 启发式函数,也就是影响广搜或者 dijkstra 从容器(队列)里取元素的优先顺序。BFS 是没有目的性的 一圈一圈去搜索, 而 A * 是有方向性的去搜索,关键在于启发式函数。
由于从队列里取出什么元素,接下来就是从哪里开始搜索。所以启发式函数主要影响队列里元素的排序!对队列里节点进行排序,就需要给每一个节点权值,权值F = G(起点达到目前遍历节点的距离) + H(目前遍历的节点到达终点的距离)
本题的图是无权网格状,在计算两点距离通常有如下三种计算方式:
- 曼哈顿距离,计算方式: d = abs(x1-x2)+abs(y1-y2)
- 欧氏距离(欧拉距离) ,计算方式:d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
- 切比雪夫距离,计算方式:d = max(abs(x1 - x2), abs(y1 - y2))
本题,采用欧拉距离才能最大程度体现 点与点之间的距离。使用欧拉距离计算 和 广搜搜出来的最短路的节点数是一样的。
计算出来 F 之后,按照 F 的 大小选择出队列的节点。可以使用 优先级队列,每次出队列就是F最小的节点。
代码如下:
import java.util.PriorityQueue;
import java.util.Scanner;public class Main {// 定义一个存储移动步数的数组static int[][] moves = new int[1001][1001];// 定义骑士的移动方向static int[][] dir = {{-2, -1}, {-2, 1}, {-1, 2}, {1, 2}, {2, 1}, {2, -1}, {1, -2}, {-1, -2}};static int b1, b2; // 目标位置// 定义骑士的状态static class Knight implements Comparable<Knight> {int x, y; // 当前坐标int g, h, f; // G, H, F 值@Overridepublic int compareTo(Knight k) { // 重载比较方法,以便优先队列可以排序return Integer.compare(this.f, k.f);}}// 估算函数,使用欧几里得距离的平方static int Heuristic(Knight k) {return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2); // 省略开根号以提高精度}// A* 算法实现static void astar(Knight k) {PriorityQueue<Knight> que = new PriorityQueue<>(); // 创建优先队列que.add(k); // 将起始节点加入队列while (!que.isEmpty()) {Knight cur = que.poll(); // 取出队列中优先级最高的节点// 如果到达目标位置,则结束搜索if (cur.x == b1 && cur.y == b2) {break;}// 遍历所有可能的骑士移动for (int i = 0; i < 8; i++) {Knight next = new Knight(); // 创建下一个节点next.x = cur.x + dir[i][0]; // 更新 x 坐标next.y = cur.y + dir[i][1]; // 更新 y 坐标// 检查下一个位置是否在有效范围内if (next.x < 1 || next.x > 1000 || next.y < 1 || next.y > 1000) {continue;}// 检查该位置是否已经访问过if (moves[next.x][next.y] == 0) {moves[next.x][next.y] = moves[cur.x][cur.y] + 1; // 更新步数// 计算 G, H 和 F 值next.g = cur.g + 5; // 统一不开根号以提高精度next.h = Heuristic(next);next.f = next.g + next.h;que.add(next); // 将下一个节点加入队列}}}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(); // 读取测试用例的数量while (n-- > 0) {int a1 = scanner.nextInt(); // 起始 x 坐标int a2 = scanner.nextInt(); // 起始 y 坐标b1 = scanner.nextInt(); // 目标 x 坐标b2 = scanner.nextInt(); // 目标 y 坐标// 清空步数数组for (int i = 0; i < moves.length; i++) {for (int j = 0; j < moves[i].length; j++) {moves[i][j] = 0;}}// 初始化起始节点Knight start = new Knight();start.x = a1;start.y = a2;start.g = 0;start.h = Heuristic(start);start.f = start.g + start.h;// 执行 A* 算法astar(start);// 输出到达目标位置的步数System.out.println(moves[b1][b2]);}scanner.close(); // 关闭扫描器}
}相关文章:
)
day60 图论章节刷题Part10(Floyd 算法、A * 算法)
Floyd 算法 思路:本题是多源最短路问题,使用Floyd算法求解。Floyd 算法对边的权值正负没有要求,核心思想是动态规划。 我们使用动规五部曲来理解和应用Floyd算法: 1、确定dp数组(dp table)以及下标的含义…...

UI架构解说
UI(用户界面,User Interface) 是指用户与软件或硬件系统进行交互的界面。 它是用户与系统之间的桥梁,允许用户通过视觉元素、交互组件和反馈机制来操作和控制应用程序或设备。 UI 设计的目标是提供直观、易用和愉悦的用户体验&a…...
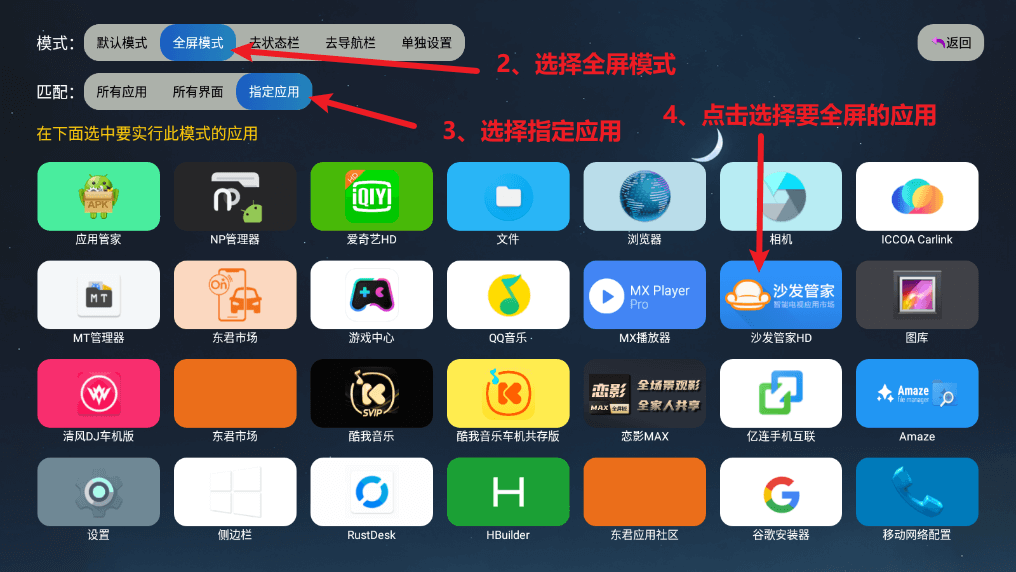
车机安装第三方软件实现打开软件全屏教程
简介 越来越多的车友实现安装第三方软件了,但是有的车机的状态栏或者导航栏会遮挡安装的第三方软件。这样的话,第三方软件就会显示不全,体验感非常不好。所以,下面我教一下大家如何使用东君应用管家来实现打开第三方软件全屏。 全…...
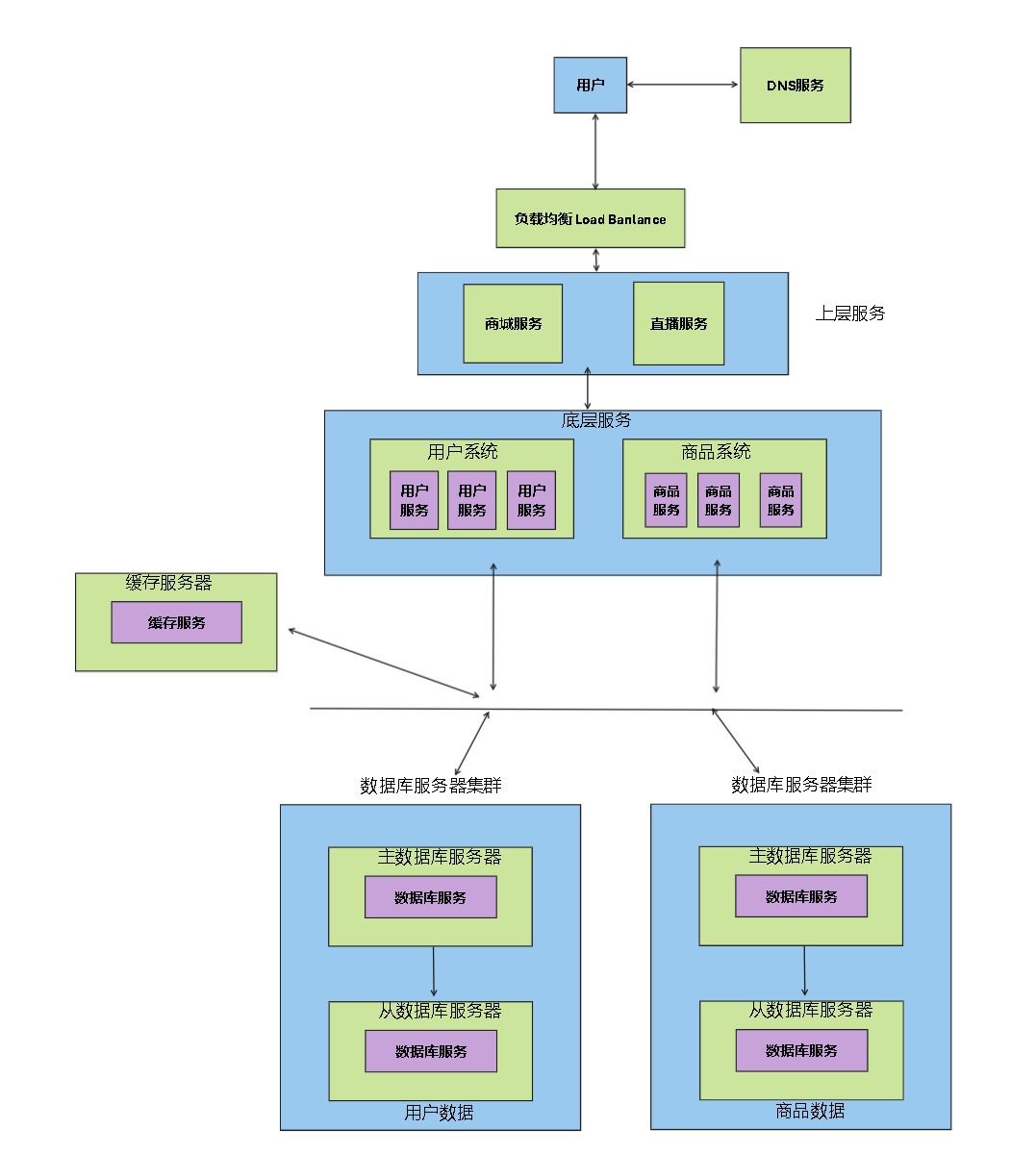
八大技术架构与演进2
垂直分库架构 当数据量不断增大,大量的数据都存储在一个库中就已经不太够用了,这时候就可以讲不同的数据分类别存储Mycat也支持在大表拆分为小标的情况下进行访问 但是这种做法其实是增加了数据库的运维难度,这种其实也就叫做分布式数据库&…...

ReactPress技术揭秘
ReactPress Github项目地址:https://github.com/fecommunity/reactpress 欢迎Star。 一、引言 ReactPress是一个基于React构建的开源发布平台,它不仅可以帮助用户在支持React和MySQL数据库的服务器上快速搭建自己的博客或网站,还能作为一个…...

Javascript高级—如何实现一个类型判断函数?
实现一个类型判断函数 判断null判断基础类型使用Object.prototype.toString.call(target)来判断引用类型 [!NOTE] 注意: 一定是使用call来调用,不然是判断的Object.prototype的类型 之所以要先判断是否为基本类型是因为:虽然Object.prototyp…...

asitop macOS 终端 性能监控
macOS 终端 性能监控 安装 pip python3 -m ensurepip# pip3 --version pip 21.2.4安装 asitop pip3 install asitop运行 sudo asitop参考 asitopgithub asitopHow to Install pip on Mac...

Unity学习笔记(4):人物和基本组件
文章目录 前言开发环境新增角色添加组件RigidBody 2D全局项目设置Edit 给地图添加碰撞体 总结 前言 今天不加班,有空闲时间。争取一天学一课,养成习惯 开发环境 Unity 6windows 11vs studio 2022Unity2022.2 最新教程《勇士传说》入门到进阶ÿ…...

【深圳大学/大学物理实验2】弗兰克-赫兹实验预习题参考
一、单选题 共 13 小题 共 78 分 1. (6分)第一栅极电压UG1、第二栅极电压UG2和减速电压UP的作用分别是( ) 学生答案:C √ A. 使电子加速,消除阴极电子散射,使电子减速 B. 产生并加速电子,使电子加速&…...

vue2.7.14 + vant + vue cli脚手架转vite启动运行问题记录
文章目录 前言方案一(借用插件转换)启动命令,转换方案一转换遇到的问题 方案二(手动调整)方案两者对比小结 前言 vue cli 脚手架转成vite启动 简单说说这个项目的一些底层基本结构哈,以及写这篇博客的目的…...

Java基础-内部类与异常处理
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 一、Java 内部类 什么是内部类? 使用内部类的优点 访问局部变量的限制 内部类和继承 内部…...

vue2或vue3的name属性有什么作用?
在 Vue.js(无论是 Vue 2 还是 Vue 3)中,组件的 name 属性有几个重要的用途。虽然它不是必须的,但在某些情况下非常有用。以下是 name 属性的一些主要作用: 1. 调试工具 Vue Devtools 和其他调试工具会使用组件的 nam…...

【FOC进阶日记】实战篇③ 电机关键数据采集方法
作者 | 量子君 微信公众号 | 极客工作室 【FOC进阶日记】专栏目录 第一章 实战篇① FOC与SVPWM详解 第二章 实战篇② 自发电控制算法 第三章 实战篇③ 电机关键数据采集方法 文章目录 前言一、M法(从路程入手):二、T法(从时间入手)三、M/T测速法:四、实现过程:总结前言…...

XSS安全基础
欢迎关注公众号【测试开发备忘录】,交流学习经验 XSS 类型: 反射型XSS:简单的把用户输入的数据“反射”给浏览器,将恶意链接嵌入,非持久; 存储型XSS:把用户输入的数据“存储”在服务端…...
)
【计网不挂科】计算机网络期末考试——【选择题&填空题&判断题&简述题】试卷(3)
前言 大家好吖,欢迎来到 YY 滴计算机网络 系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 本博客主要内容,收纳了一部门基本的计算机网络题目,供yy应对期中考试复习。大家可以参考 本章是去答案版本。带答案的版本在下…...

516.最长回文子序列
刷算法题: 第一遍:1.看5分钟,没思路看题解 2.通过题解改进自己的解法,并且要写每行的注释以及自己的思路。 3.思考自己做到了题解的哪一步,下次怎么才能做对(总结方法) 4.整理到自己的自媒体平台。 5.再刷重复的类…...

leetcode hot100【LeetCode 114.二叉树展开为链表】java实现
LeetCode 114.二叉树展开为链表 题目描述 给你二叉树的根结点 root ,请你将它展开为一个单链表: 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。 展开后的单链表应该与…...

SpringMVC学习记录(二)之接收数据
SpringMVC学习记录(二)之接收数据 一、快速搭建SpringMVC框架1、配置分析2、准备项目3、Controller声明4、Spring MVC核心组件配置类5、SpringMVC环境搭建6、启动测试 二、SpringMVC接收数据1、访问路径设置1)精准路径匹配2)模糊路…...

C语言串讲-3之函数和数组
1.函数名是一个指针,保存函数地址入口。函数名是函数的入口地址。函数的入口地址称为函数指针。 2.传参--本质是创建副本 (1)实参与形参 (2)值传递,指针传递,引用传递 …...

设计模式-状态模式(State)
允许一个对象内部状态改变时改变它的行为,对象看起来似乎修改了它的类 问题: 状态模式和有限状态机紧密相关。其主要思想是程序在任意时刻仅可处于几种有限的状态中。 在任何一个特定状态中, 程序的行为都不相同, 且可瞬间从一个…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
