Leetcode刷题笔记14
136. 只出现一次的数字
136. 只出现一次的数字 - 力扣(LeetCode)

核心思想:按位异或运算
利用按位异或运算的性质来解决这个问题:
异或运算的性质:
a ^ a = 0:相同的数异或结果为0。
a ^ 0 = a:任意数与0异或结果为该数本身。
交换律和结合律:a ^ b ^ a = (a ^ a) ^ b = 0 ^ b = b。
由于数组中除了一个数只出现一次,其他数都出现两次,根据异或运算的性质,这些成对出现的数会互相抵消变成0,
最后剩下的就是那个只出现一次的数。
示例运行
假设 nums = [2, 2, 1],我们来看看代码如何运行:
初始 value = 0。
遍历数组:
value ^= 2:value = 0 ^ 2 = 2
value ^= 2:value = 2 ^ 2 = 0
value ^= 1:value = 0 ^ 1 = 1
最终 value 的值为1,返回1。
这个结果符合预期,证明代码是正确的。
通过异或运算,可以在线性时间内(O(n))找到唯一只出现一次的数字,
并且只使用常量级别的额外空间(O(1))。这个方法既高效又简洁。
代码:C++
class Solution {
public:int singleNumber(vector<int>& nums) {int ret=0;for(auto i: nums) ret^=i;return ret;}
};118. 杨辉三角
118. 杨辉三角 - 力扣(LeetCode)

杨辉三角的特点是每个数是它上方两个数之和。
核心思想
杨辉三角的特点是,每个位置的值等于其上方相邻两个元素之和。使用这种递归关系,从上往下逐行构造,每一行的首尾元素是固定的 1,中间的元素通过前一行的值计算得到。
思路
- 建立结构:构造一个二维数组,将其大小设置为
n行,逐行填充杨辉三角的值。 - 固定边界条件:每一行的首尾元素都是
1,可以直接赋值。 - 动态填充中间元素:对于每行的中间元素,利用递推公式
triangle[i][j] = triangle[i - 1][j - 1] + triangle[i - 1][j],计算当前行的每个位置值。 - 输出结果:生成所需行数的杨辉三角,输出作为二维数组。
代码:C++
class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> vv;vv.resize(numRows);for(size_t i=0;i<vv.size();++i){vv[i].resize(i+1, 0); // 第0行开一个0,第1行开2个0...// 第一个和最后一个是1vv[i].front() = 1;vv[i].back() = 1;}for(size_t i=0;i<vv.size();++i){for(size_t j=0; j<vv[i].size(); ++j){if(vv[i][j]==0){vv[i][j]=vv[i-1][j] + vv[i-1][j-1];}}}return vv;}
};//class Solution {
//public:
// vector<vector<int>> generate(int numRows) {
// vector<vector<int>> vv; // 声明一个二维向量vv,存储杨辉三角的每一行
// vv.resize(numRows); // 调整vv的大小为numRows行
// for (size_t i = 0; i < vv.size(); ++i) { // 遍历每一行
// vv[i].resize(i + 1, 0); // 每一行有i+1个元素,初始化为0
// vv[i].front() = 1; // 每一行的第一个元素为1
// vv[i].back() = 1; // 每一行的最后一个元素为1
// }
// for (size_t i = 0; i < vv.size(); ++i) { // 再次遍历每一行
// for (size_t j = 0; j < vv[i].size(); ++j) { // 遍历每一行的每个元素
// if (vv[i][j] == 0) { // 如果当前元素是0,表示它需要计算
// vv[i][j] = vv[i - 1][j - 1] + vv[i - 1][j]; // 当前元素是它左上和右上的元素之和
// }
// }
// }
// return vv; // 返回生成的杨辉三角
// }
//};26. 删除有序数组中的重复项
26. 删除有序数组中的重复项 - 力扣(LeetCode)

核心思想
这道题的核心思想是利用双指针在排序数组中去除重复项。一个指针 dst 用于记录去重后的数组位置,另一个指针 src 用于遍历整个数组。由于数组已排序,所以重复的元素必然是相邻的。通过逐个比较和移动指针,可以在不使用额外空间的情况下完成去重。
思路
- 设置指针:初始化
src和dst两个指针,均指向数组的起始位置。 - 遍历数组:使用
src指针遍历整个数组:- 如果
src和dst指向的元素相同,则说明遇到重复元素,仅移动src指针。 - 如果
src和dst指向的元素不同,则说明遇到新的元素,将src的值赋给dst + 1,然后同时移动src和dst指针。
- 如果
- 调整数组长度:在遍历结束后,将数组的长度调整为
dst + 1。 - 返回长度:返回去重后的数组长度。
代码:C++
class Solution {
public:int removeDuplicates(vector<int>& nums) {int src=0;int dst=0;while(src < nums.size()){if(nums[src] == nums[dst]) // 如果 src 和 dst 指向的元素相同,说明是重复元素,移动 src 指针{++src;}else // 如果 src 和 dst 指向的元素不同,将 src 的值复制到 dst + 1 位置,同时移动 src 和 dst 指针{nums[++dst] = nums[src++];}}nums.resize(dst+1);return dst + 1;}
};17. 电话号码的字母组合
17. 电话号码的字母组合 - 力扣(LeetCode)

核心思想
利用回溯(Backtracking)方法,根据数字字符串中的每个数字,将其映射到对应的字母集合,通过递归逐步生成所有可能的组合。这种递归方法允许我们逐一生成不同长度的组合,当达到字符串的末尾时,将组合加入结果列表。
思路
- 建立映射:初始化一个数组
numToStr,存储每个数字对应的字母字符串。例如,2对应 "abc",3对应 "def",依此类推。 - 递归生成组合:定义一个递归函数
Combine,用于将当前数字对应的字母添加到组合字符串中:- 如果已经处理到数字字符串的末尾,将当前组合字符串加入结果列表。
- 否则,获取当前数字对应的字母集合,对每个字母,递归调用
Combine生成下一个字符的组合。
- 边界处理:在递归开始前,判断输入是否为空字符串,如果为空则直接返回空列表。
- 返回结果:递归结束后,返回存储所有组合的列表。
代码:C++
class Solution {char* numToStr[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};// string numToStr[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public:void Combine(string digits, int di, vector<string>& retV, string combineStr){if(di == digits.size()){retV.push_back(combineStr);return;}// 递归// 取数字字符映射的字符串int num = digits[di] - '0';string str = numToStr[num];for(auto ch : str){// di+1就会往下一层走Combine(digits, di+1, retV, combineStr+ch);}}vector<string> letterCombinations(string digits) {vector<string> v;if(digits.empty()){return v;}string str;Combine(digits, 0, v, str);return v;}
};相关文章:

Leetcode刷题笔记14
136. 只出现一次的数字 136. 只出现一次的数字 - 力扣(LeetCode) 核心思想:按位异或运算 利用按位异或运算的性质来解决这个问题: 异或运算的性质: a ^ a 0:相同的数异或结果为0。 a ^ 0 a:…...

PHP图书绘本借阅管理系统小程序源码
📚 图书绘本借阅管理系统:打造孩子的阅读乐园 📚 🏷️ 引言:为什么我们需要图书绘本借阅管理系统? 在孩子的成长旅程中,阅读是不可或缺的一部分。然而,面对琳琅满目的图书和绘本&a…...

【JavaWeb】JavaWeb入门之XML详解
目录 1.XML介绍 1.1.XML概述 1.1.1.什么是XML 1.1.2.XML的作用 1.1.3.XML与HTML的比较 1.1.4.XML和properties(属性文件)比较 1.1.5.W3C组织 1.2.XML语法概述 1.2.1.XML文档展示 1.2.2.XML文档的组成部分 1.3.XML文档声明 1.3.1.什么是XML文…...

JS手写-this绑定实现
在 JavaScript 中,bind、call 和 apply 方法都可以用来改变函数的 this 指向。下面我们将分别实现这些方法的简单版本。 1. 实现 bind bind 方法创建一个新的函数,在调用时设置 this 值,并返回这个新的函数。 Function.prototype.myBind …...

【时间之外】IT人求职和创业应知【31】
目录 新闻一:2024年“秦创原沣东杯”陕西省科技工作者创新创业大赛颁奖仪式暨沣东新城机器人产业发展大会盛大启幕 新闻二:声网CEO赵斌:RTE将成为生成式AI时代AI Infra的关键部分 新闻三:“5G工业互联网”融合应用试点城市名单…...

如何使用ffmpeg命令行进行录屏
录屏软件,我们去网上下载,发现有很多软件都是要收费的!但是录屏功能很难做吗?为啥都需要收费呢? 于是我整了个小demo,用于实现基础的屏幕录制功能。 思路很简单,考虑到 FFMpeg.exe是一个非常成…...

ODOO学习笔记(8):模块化架构的优势
灵活性与可定制性 业务流程适配:企业的业务流程往往因行业、规模和管理方式等因素而各不相同。Odoo的模块化架构允许企业根据自身的具体业务流程,选择和组合不同的模块。例如,一家制造企业可以启用采购、库存、生产和销售模块,并通…...

数字IC后端实现之Innovus specifyCellEdgeSpacing和ICC2 set_placement_spacing_rule的应用
昨天帮助社区IC训练营学员远程协助解决一个Calibre DRC案例。通过这个DRC Violation向大家分享下Innovus和ICC2中如何批量约束cell的spacing rule。 数字IC后端手把手实战教程 | Innovus verify_drc VIA1 DRC Violation解析及脚本自动化修复方案 下图所示为T12nm A55项目的Ca…...

每日小练:Day2
1.乒乓球筐 题目链接:乒乓球筐__牛客网 题目描述: 这道题主要考察B盒是不是A盒的子集,我们可以通过哈希表来做 单哈希表 import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main {public stat…...

ubuntu 安装kafka-eagle
上传压缩包 kafka-eagle-bin-2.0.8.tar.gz 到集群 /root/efak 目录 cd /root/efak tar -zxvf kafka-eagle-bin-2.0.8.tar.gz cd /root/efak/kafka-eagle-bin-2.0.8 mkdir /root/efakmodule tar -zxvf efak-web-2.0.8-bin.tar.gz -C /root/efakmodule/ mv /root/efakmodule/efak…...

深入理解指针
在初步了解了指针的用法之后,我们可以想一想,既然一个变量有地址,而且在上一篇文章中我们知道了一个数组也有地址,那么函数、字符串这些东西有没有地址呢?如果有,那这些地址有什么用?我们又要怎…...
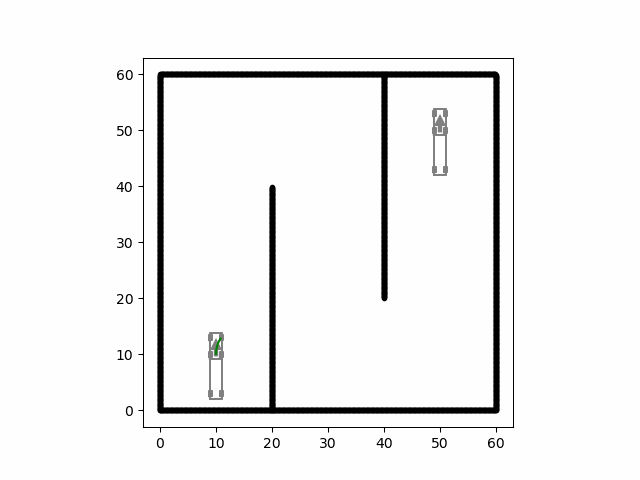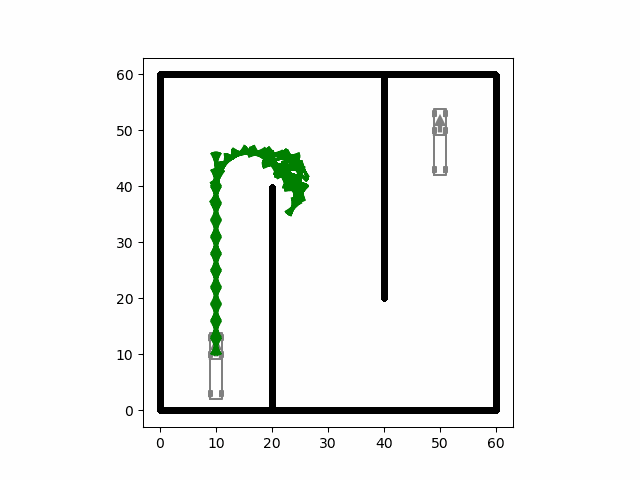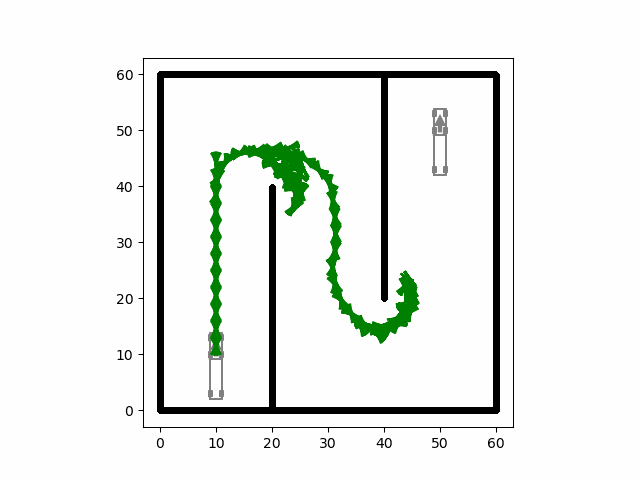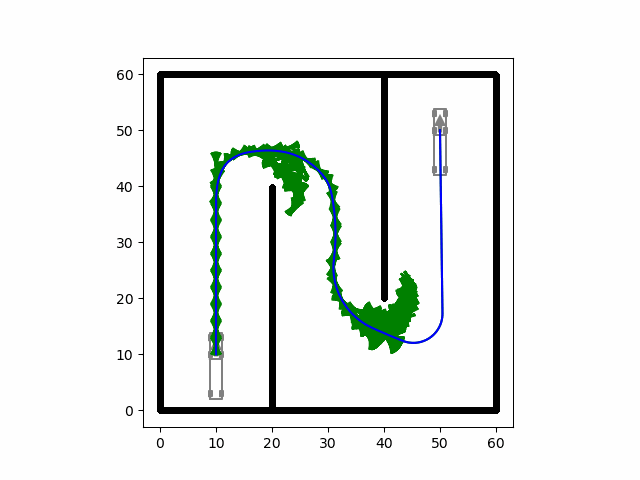
自动驾驶合集(更新中)
文章目录 车辆模型控制路径规划 车辆模型 车辆模型基础合集 控制 控制合集 路径规划 规划合集...

Chapter 14 scoped样式以及data函数
欢迎大家订阅【Vue2Vue3】入门到实践 专栏,开启你的 Vue 学习之旅! 文章目录 1 scoped样式1.1 全局样式1.2 局部样式1.3 工作原理2 data函数 1 scoped样式 1.1 全局样式 全局样式是指作用于整个应用程序的样式,不论在哪个组件中定义&#x…...

Golang | Leetcode Golang题解之第557题反转字符串中的单词III
题目: 题解: func reverseWords(s string) string {length : len(s)ret : []byte{}for i : 0; i < length; {start : ifor i < length && s[i] ! {i}for p : start; p < i; p {ret append(ret, s[start i - 1 - p])}for i < le…...

区块链技术在电子政务中的应用
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 区块链技术在电子政务中的应用 区块链技术在电子政务中的应用 区块链技术在电子政务中的应用 引言 区块链技术概述 定义与原理 发…...

Simulink中Matlab function使用全局变量
目录 一. 引言二. 普通Matlab function使用全局变量三. Simulink中的Matlab function使用全局变量四. 如何利用Matlab function的全局变量施加随机噪声 一. 引言 最近发现了之前仿真中的一个问题,记录一下备忘。 Matlab function中有时候需要用到全局变量…...

WPF-控件的属性值的类型转化
控件的属性值需要转成int、double进行运算的,可以使用一下方法 页面代码 <StackPanel Margin"4,0,0,0" Style"{StaticResource Form-StackPanel}"> <Label Content"替换后材料增加金额ÿ…...

海思Hi3516DV300上播放G711U音频文件
在海思Hi3516DV300芯片运行Linux系统下,可通过如下函数来实现G711U音频文件的播放: int ADecPlayVoiceFile(const char* filename) {FILE* pfd;AUDIO_STREAM_S stStream;HI_S32 s32Ret,length,decLength,allLength 0,aChn 0;HI_U8 buf[SAMPLE_AUDIO_P…...
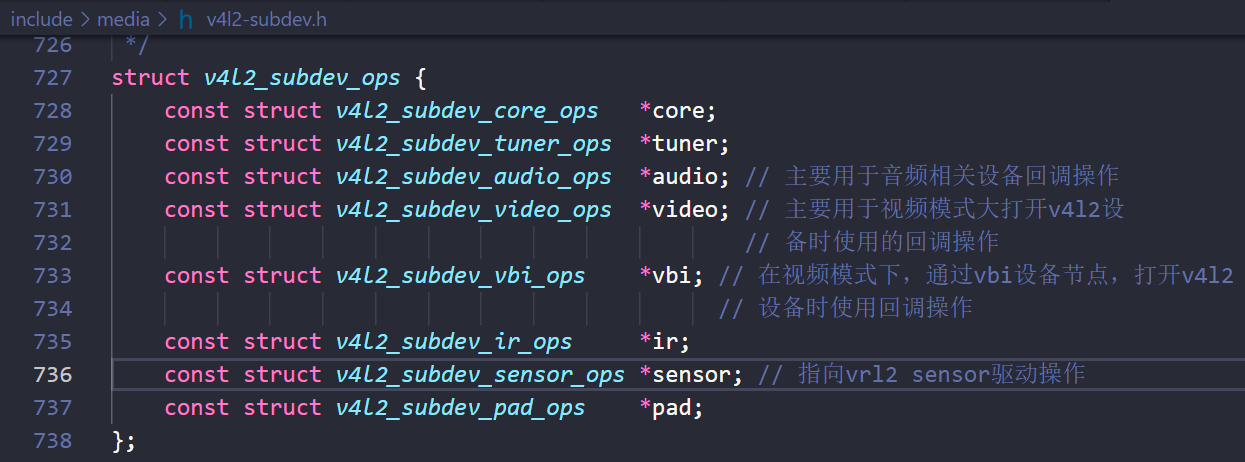
Linux源码阅读笔记-V4L2框架基础介绍
V4L2视频设备驱动基础 V4L2 是专门为 Linux 设备设计的整套视频框架(其主要核心在 Linux 内核,相当于 Linux 操作系统上层的视频源捕获驱动框架)。为上层访问系统底层的视频设备提供一个统一的标准接口。V4L2 驱动框架能够支持多种类型设备&…...

列表(list)
一、前言 本次博客主要讲解 list 容器的基本操作、常用接口做一个系统的整理,结合具体案例熟悉自定义内部排序方法的使用。如有任何错误,欢迎在评论区指出,我会积极改正。 二、什么是list list是C的一个序列容器,插入和删除元素…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
