室内定位论文精华-无人机与机器人在地下与室内环境中的自主导航与定位新技术
天文导航算法在低成本视觉系统中的应用
关键词
天文导航;自主无人机;GNSS拒止环境;稳定成像系统;星图识别;姿态估计;位置估算
研究问题
现代无人驾驶飞行器(UAV)中,很少使用天文学导航技术。传统的天文学导航依赖于稳定的成像系统,这不仅体积大且重量重,难以满足飞行器的性能需求。另外,在没有全球定位系统(GNSS)信号的情况下,如何实现精确和可靠的天文导航是一个重要的问题。
方法
提出了一种基于低成本视觉系统的天文导航算法。该方法结合了星图识别技术和姿态估计技术,使用无人机携带的小型稳定成像设备来捕捉星空图像,并通过软件分析这些图像以确定位置和方向。具体步骤如下:
- 使用摄像头拍摄天空中的恒星。
- 应用计算机视觉算法进行星图匹配,将所摄图像与已知星图数据库对比以识别特定的星星或星座。
- 依据识别到的星空信息来估计飞行器的姿态(姿态角包括俯仰角、偏航角和滚动角)和位置。
创新点
- 算法优化:通过采用先进的计算机视觉技术和图像处理技术,使得星图匹配过程更
相关文章:

室内定位论文精华-无人机与机器人在地下与室内环境中的自主导航与定位新技术
天文导航算法在低成本视觉系统中的应用 关键词 天文导航;自主无人机;GNSS拒止环境;稳定成像系统;星图识别;姿态估计;位置估算 研究问题 现代无人驾驶飞行器(UAV)中,很少使用天文学导航技术。传统的天文学导航依赖于稳定的成像系统,这不仅体积大且重量重,难以满足…...

Java 中如何自定义一个类加载器,加载自己指定的类?
文章目录 为什么要自定义类加载器?类加载器的基本原理自定义类加载器的步骤1. 继承 ClassLoader 类2. 编写 findClass 方法 代码示例代码解释 使用自定义类加载器加载类执行结果注意事项总结推荐阅读文章 在 Java 中,类加载器(ClassLoader&am…...

LeetCode【0037】解数独
本文目录 1 中文题目2 求解方法:递归回溯法2.1 方法思路2.2 Python代码2.3 复杂度分析 3 题目总结 1 中文题目 编写一个程序,通过填充空格来解决数独问题。数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只…...

计算机视觉 ---常见图像文件格式及其特点
常见的图像文件格式及其特点如下: JPEG(Joint Photographic Experts Group) 特点: 有损压缩:通过丢弃一些图像数据来实现高压缩比,能显著减小文件大小,适合用于存储照片等色彩丰富的图像。但过…...

Cent OS-7的Apache服务配置
WWW是什么? WWW(World Wide Web,万维网)是一个全球性的信息空间,其中的文档和其他资源通过URL标识,并通过HTTP或其他协议访问。万维网是互联网的一个重要组成部分,但它并不是互联网的全部。互联…...

mysql每日一题(上升的温度,date数据的计算)
日期之间的运算 日期类型的加法运算 data_add(now_data,interval 1 month) select date_add(now(), interval 1 day); -- 加1天 select date_add(now(), interval 1 hour); -- 加1小时 select date_add(now(), interval 1 minute); -- 加1分钟 select date_add(now(), inter…...

前端人之网络通信概述
前端人之网络通信概述 介绍网络七层模型物理层链路层网络层传输层应用层 介绍 互联网的核心技术就是一系列协议,总称“互联网协议”,对电脑如何连接和组网作出详细的规定,理解了这些协议就理解了互联网的原理。 网络七层模型 互联网完成数…...

Python从0到100(七十二):Python OpenCV-OpenCV实现手势音量控制(文末送书)
前言: 零基础学Python:Python从0到100最新最全教程。 想做这件事情很久了,这次我更新了自己所写过的所有博客,汇集成了Python从0到100,共一百节课,帮助大家一个月时间里从零基础到学习Python基础语法、Pyth…...

【云原生开发】K8S多集群管理系统成果展示
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

spring boot项目打成war包部署
1.修改pom.xml 在 pom.xml 里设置 <packaging>war</packaging>2.移除嵌入式tomcat插件 在 pom.xml 里找到spring-boot-starter-web依赖,在其中添加如下代码, <dependency><groupId>org.springframework.boot</groupId>&l…...
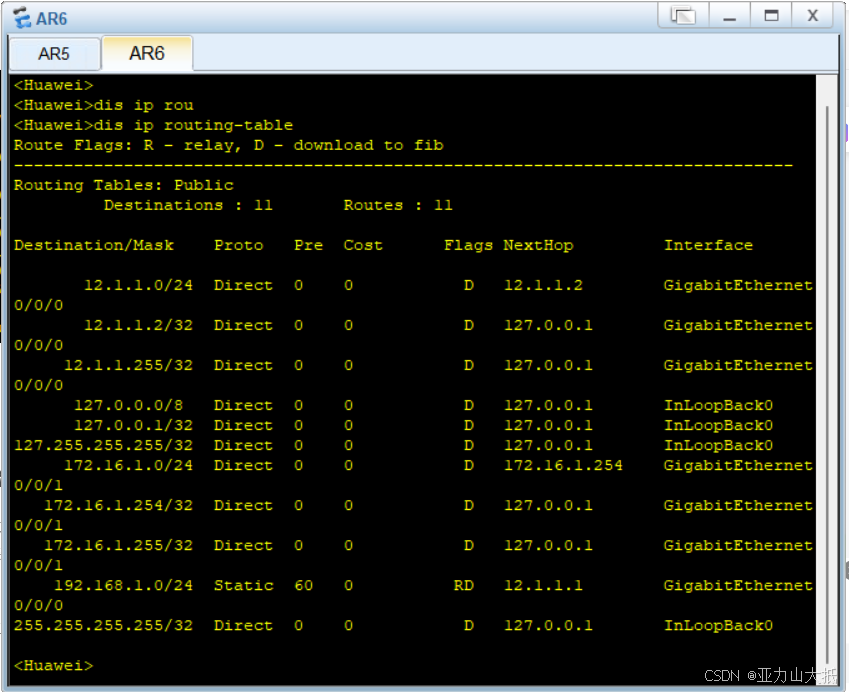
网络学习第四篇
引言: 我们在第三篇的时候出现了错误,我们要就行排错,那么我们要知道一下怎么配置静态路由实现ping通,这样子我们才知道下一跳到底是什么,为什么这样子做。 实验目的 理解和掌握静态路由的基本概念和配置方法。 实…...

【资料】网络安全风险评估报告,风险管理报告,网络安全风险管理计划,网络安全网络安全能力验证报(Word原件)
一、概述 1.1工作方法 1.2评估依据 1.3评估范围 1.4评估方法 1.5基本信息 二、资产分析 2.1 信息资产识别概述 2.2 信息资产识别 三、评估说明 3.1无线网络安全检查项目评估 3.2无线网络与系统安全评估 3.3 ip管理与补丁管理 3.4防火墙 四、威胁细类分析 4.1威胁…...

Django基础用法+Demo演示
Django快速上手 参考: Django快速上手 再写几个页面 编辑demo1/urls.py, 添加URL和视图函数映射 urlpatterns [path(index/, views.index),path(user/list/, views.user_list),path(user/add/, views.user_add), ]编辑app01/views.py,添加几个函数 from djang…...

【webrtc】 RTP 中的 MID(Media Stream Identifier)
RTP 中的 MID(Media Stream Identifier) RID及其与MID的区别 cname与mid的对比【webrtc】CNAME 是rtprtcp中的Canonical Name(规范化名称) 同样都是RTP头部扩展: 基于mediasoup的最新的代码,学习,发现mid在创建RtpSendStream时是必须传递的参数: 例如 D:\XTRANS\soup\…...

React 中 为什么多个 JSX 标签需要被一个父元素包裹?
为什么多个 JSX 标签需要被一个父元素包裹? JSX 虽然看起来很像 HTML,但在底层其实被转化为了 JavaScript 对象,你不能在一个函数中返回多个对象,除非用一个数组把他们包装起来。这就是为什么多个 JSX 标签必须要用一个父元素或者…...

记录日志中logback和log4j2不能共存的问题
本文章记录设置两个日志时候,控制台直接报错 标黄处就是错误原因:1. SLF4J(W):类路径包含多个SLF4J提供程序。 SLF4J(W):找到提供程序[org.apache.logging.slf4j. net]。 SLF4J(W):找到提供程序[ch.qos.log .classi…...

第5章: 图像变换与仿射操作
图像变换和仿射操作是图像处理中常用的技术,通过旋转、缩放、平移、剪裁等操作,可以实现多种视觉效果以及数据增强。 1.1 图像旋转 1.1.1 基础旋转操作 使用 rotate() 方法可以对图像进行旋转操作,指定旋转的角度(以度为单位&am…...
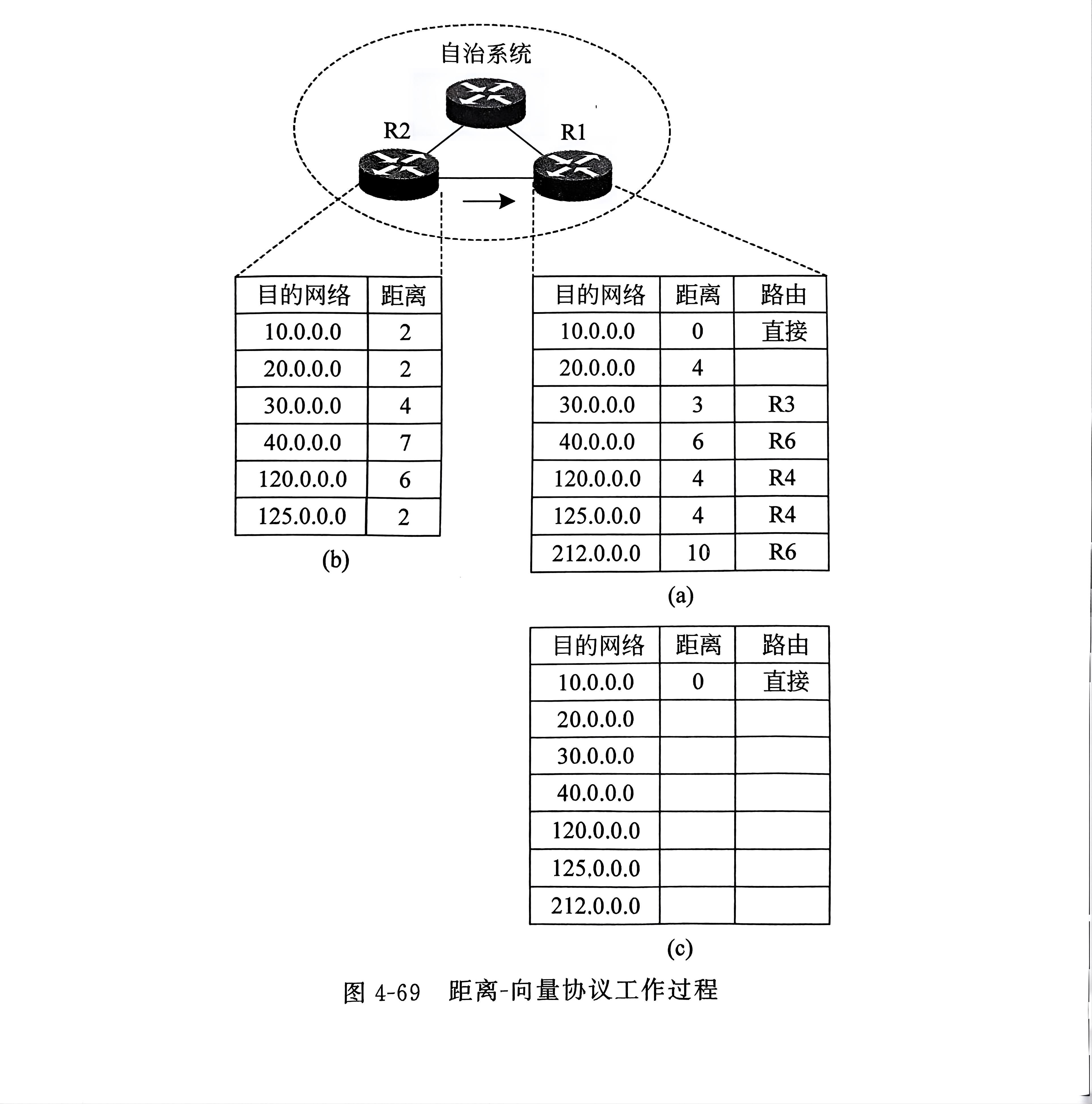
【计算机网络】【网络层】【习题】
计算机网络-传输层-习题 文章目录 13. 图 4-69 给出了距离-向量协议工作过程,表(a)是路由表 R1 初始的路由表,表(b)是相邻路由器 R2 传送来的路由表。请写出 R1 更新后的路由表(c)。…...

Scala的不可变Map常用操作
//类型:不可变,可变 //操作:添加元素,删除元素,查询元素,删除元素,遍历 object map {def main(args: Array[String]): Unit {//不可变Mapval map1 Map("鄂"->"湖北省"…...

nginx配置负载均衡详解
在现代的 web 应用中,负载均衡是确保高可用性、可扩展性和稳定性的关键技术之一。Nginx 是一个非常流行的反向代理服务器和负载均衡器,它支持多种负载均衡策略,能够帮助将客户端的请求分发到多个后端服务器,以提高系统的整体性能和…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
