软间隔支持向量机

软间隔支持向量机

​ 我们先直接给出软间隔支持向量机的形式：
$$\begin{gathered} P=\underset{\omega ,b,\zeta }{\min }\frac{1}{2}\Vert \omega {\Vert }_2^2-C\sum _{i=1}^m{\zeta }_i \\ s.t.y_i(\omega x_i+b)\ge 1-{\zeta }_i,i=1,2,\mathrm{3..}m \\ {\zeta }_i\ge 0,i=1,2,\mathrm{3..}m \end{gathered}$$

​ 线性可分的对立面一定是线性不可分，这个时候无论如何改变超平面与支持向量，数据都无法从线性可分转为线性不可分。但是对于完全杂乱的数据来说，我们往往还会遇到一种情况就是数据中存在一小部分的特异点而导致数据线性不可分，如图所示：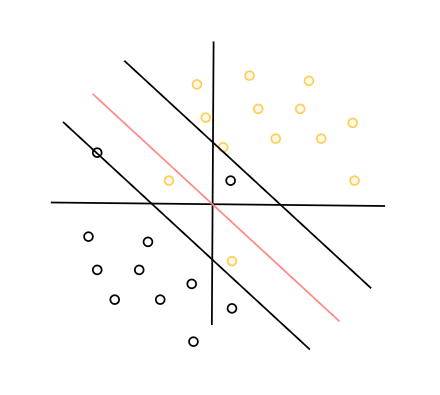

​ 在这种情况下如果直接选择线性不可分的算法反而会让我们的问题更复杂，同时也可能导致过拟合的问题，那么我们不妨放松一定的硬间隔限制，允许错误分类。或者说，允许尽可能少的错误分类，从而获得更好的泛化效果。

​ 对于正分类点的错误分类来说，我们可以划分为三种，如图上Case1，Case2，Case3三个点，分别代表了允许特异点进入超平面与正支持向量之间，允许特异点进入超平面与负支持向量之间，允许特异点进入负分类区间。

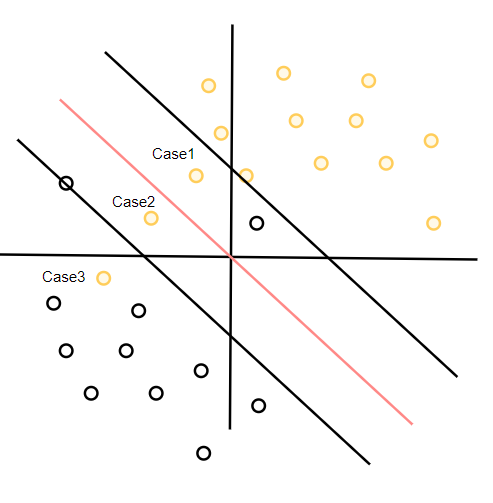
​ 针对三种情况我们分别分析，同时引入松弛变量。引入松弛变量的目的就是为了放松硬间隔的区间限制，让原本只能出现在过支持向量与超平面平行的平面正侧的点可以出现在其他地方，为了方便分析我们假设最优超平面如图所示$\omega X+b=0$保持不动，研究如何调整限制条件，以允许线性不可分样本可以存在。

1. Case1

​ 我们将Case1的特征向量代入超平面得到$\omega X_c+b=P$，显然$0<P<1$，此时$0\le Y_c(\omega X_c+b)<1$

​ 原来我们要求正分类点在正支持向量右上方的时候限制条件为：$Y_c(\omega X_c+b)\ge 1$

​ 将Case1的点纳入限制范围，则限制条件变为$Y_c(\omega X_c+b)\ge 0$

​ 我们假设松弛变量$0\le \zeta \le 1$，那么限制条件就可以转换为：$Y_c(\omega X_c+b)\ge 1-\zeta$

​ 此时我们允许误分类点进入正支持向量平面与超平面之间

2. Case2

​ 我们将Case2的特征向量代入超平面得到$\omega X_c+b=P$，显然$-1<P<0$，此时$-1\le Y_c(\omega X_c+b)<0$

​ 原来我们要求正分类点在超平面右上方的时候限制条件为：$Y_c(\omega X_c+b)\ge 0$

​ 将Case2的点纳入限制范围，则限制条件变为$Y_c(\omega X_c+b)\ge -1$

​ 我们假设松弛变量$0\le \zeta \le 2$，那么限制条件就可以转换为：$Y_c(\omega X_c+b)\ge 1-\zeta$

​ 此时我们允许误分类点进入负支持向量平面与超平面之间

3. Case3

​ 我们将Case1的特征向量代入超平面得到$\omega X_c+b=P$，显然$P<-1$，此时$ Y_c(\omega X_c+b)<-1$

​ 原来我们要求正分类点在负支持向量右上方平面的时候限制条件为：$Y_c(\omega X_c+b)\ge -1$

​ 我们假设松弛变量$0\leq \zeta $，那么限制条件就可以转换为：$Y_c(\omega X_c+b) \geq 1-\zeta$

​ 此时我们允许误分类点进入负分类区间

4. 限制松弛变量

​ 之前的内容我们是从已经引入松弛变量的角度分析为什么在模型中要求${\zeta }_i\ge 0$，现在我们来分析松弛变量是如何引入目标函数的。

​ 显然我们现在对每一个特异点都设置了一个松弛变量${\zeta }_i$使得原来的模型能够容纳这些错误的情况，但是如果不对这种放松进行惩罚，在面对线性不可分的数据时，模型可以随意让样本点可以随意靠近或穿过超平面。

​ 样本点随意靠近或穿过超平面，这就忽略了我们不同类别的数据点到这个超平面的最小距离（即间隔）最大这个核心目标。因为不加限制的话，会导致几何间隔$\frac{2}{\Vert \omega \Vert }$不断的变小。

​ 那为什么会导致几何间隔$\frac{2}{\Vert \omega \Vert }$不断的变小呢？

​ 假设我们已经有超平面可以将两类数据大部分分开，则正负支持向量之间的间隔恰好为$\frac{2}{\Vert \omega \Vert }$，当我们不惩罚${\zeta }_i$，并且想要把这个数据点也正确分类。为了使$y_i(\omega x_i+b)\ge 1-{\zeta }_i{\zeta }_i\ge 0$成立，我们不得不增大${\zeta }_i$，同时调整超平面。调整超平面可能就会导致我们的几何间隔变小，这会与我们间隔最大化这个问题相违背。所以必须增加惩罚。我们为每一个松弛变量添加惩罚，同时设置一个参数可以控制惩罚的力度，进而我们就得到了：
$$\begin{gathered} P^{\ast }=\max \frac{1}{\Vert \omega \Vert }\Vert +C\sum _{i=1}^N{\zeta }_i \\ s.t.y_i(\omega x_i+b)\ge 1-{\zeta }_i,i=1,2,\mathrm{3..}N \\ {\zeta }_i\ge 0,i=1,2,\mathrm{3..}N \end{gathered}$$
​ 我们的问题其实转为了在$\omega$和松弛变量$\zeta$ 之间寻求一个平衡，而C是来控制这个平衡的程度。最终我们将问题转为我们一开始的最小化问题P。

5. 求解P

​ 根据拉格朗如对偶法构建拉格朗日函数：
$$\begin{gathered} L(\omega ,b,\zeta ,\alpha ,\mu )=\frac{1}{2}\Vert \omega {\Vert }_2^2+C\sum _{i=1}^N{\zeta }_i-\sum _{i=1}^m{\alpha }_i[y_i(\omega x_i+b)-1+{\zeta }_i]-\sum _{i=1}^m{\mu }_i{\zeta }_i \\ and \\ {\mu }_i\ge 0,{\zeta }_i\ge 0 \end{gathered}$$

​ 则优化的目标函数为：${\min }_{\omega ,b,\zeta }{\max }_{{\mu }_i,{\zeta }_i}L(\omega ,b,\zeta ,\alpha ,\mu )$

​ 符合Slater条件转为对偶问题：${\max }_{{\mu }_i,{\zeta }_i}{\min }_{\omega ,b,\zeta }L(\omega ,b,\zeta ,\alpha ,\mu )$

​ 先求最小化问题：
$$\begin{gathered} \frac{\partial L}{\partial w}=0\Rightarrow w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i \\ \frac{\partial L}{\partial b}=0\Rightarrow \sum _{i=1}^m{\alpha }_i{y}_i=0 \\ \frac{\partial L}{\partial \xi }=0\Rightarrow C-{\alpha }_i-{\mu }_i=0 \end{gathered}$$
​ 代入消去$\omega ,b$
$$L(\omega ,b,\zeta ,\alpha ,\mu )=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
​ 仔细观察这个式子会发现其实与支持向量机最终得到的公式是一样的，但是不同的是约束条件：
$$\begin{gathered} \underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j \\ s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0 \\ C-{\alpha }_i-{\mu }_i=0 \\ {\alpha }_i\ge 0(i=1,2,...,m) \\ {\mu }_i\ge 0(i=1,2,...,m) \end{gathered}$$

对于三个约束来说代入消去$\mu$可以得到唯一一个约束也就是：$0\le {\alpha }_i\le C$，然后我们就可以通过SMO算法来解出最终的$\alpha 和b$