【leetcode练习·二叉树】用「分解问题」思维解题 I
本文参考labuladong算法笔记[【强化练习】用「分解问题」思维解题 I | labuladong 的算法笔记]
105. 从前序与中序遍历序列构造二叉树 | 力扣 | LeetCode |
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
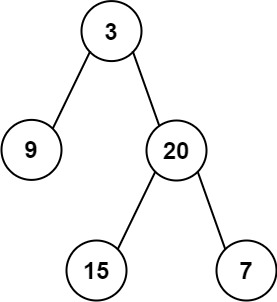
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
基本思路
构造二叉树,第一件事一定是找根节点,然后想办法构造左右子树。
二叉树的前序和中序遍历结果的特点如下:
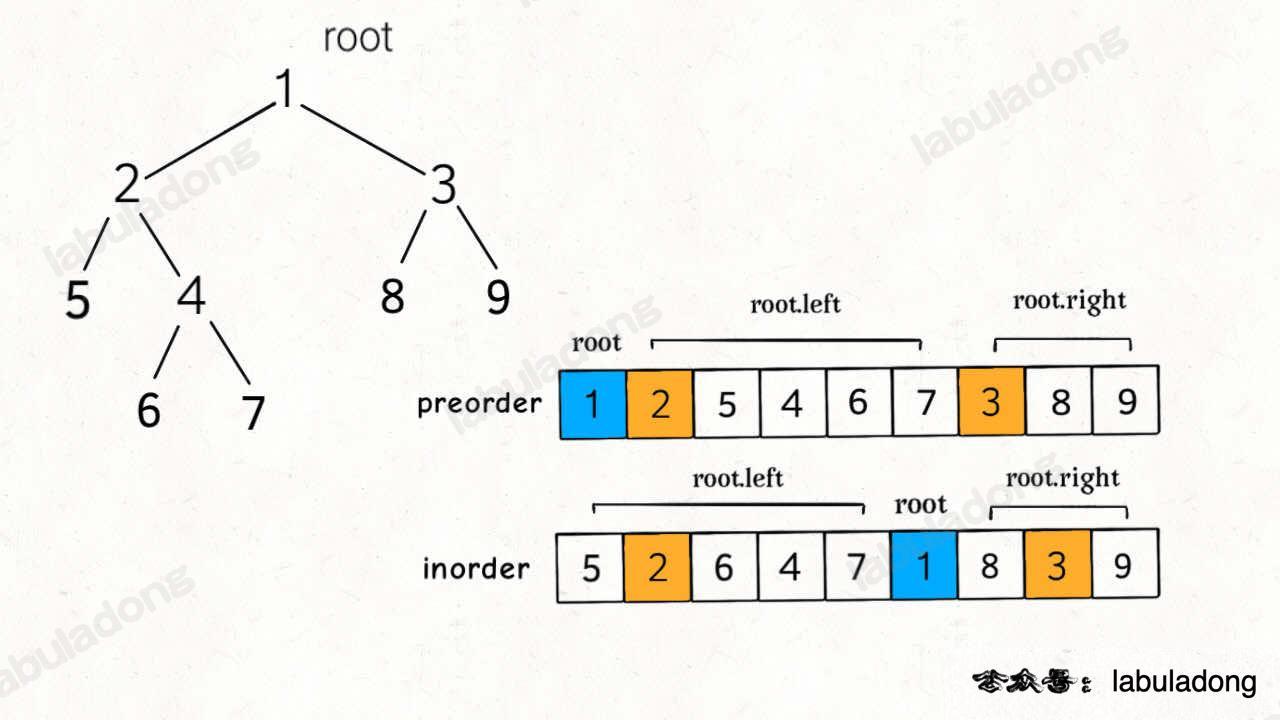
前序遍历结果第一个就是根节点的值,然后再根据中序遍历结果确定左右子树的节点。
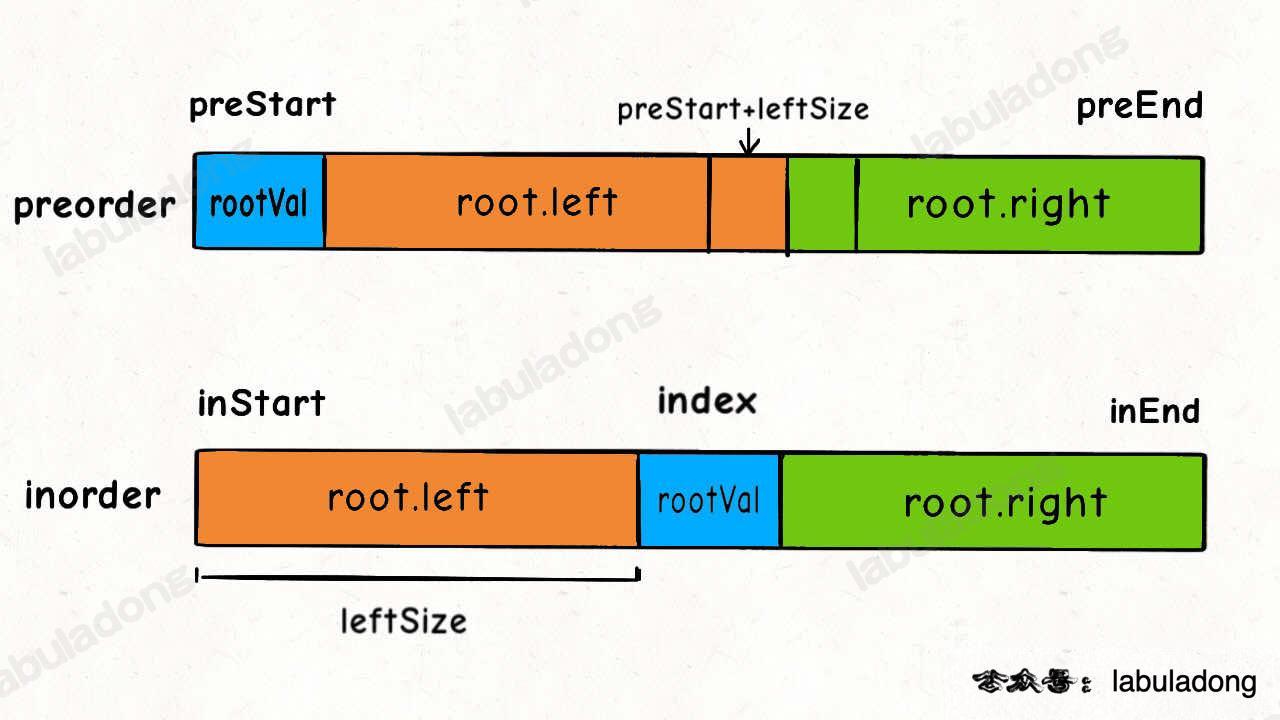
结合这个图看代码辅助理解。
详细题解
class Solution:# 存储 inorder 中值到索引的映射def __init__(self):self.valToIndex = {}def buildTree(self, preorder, inorder):for i in range(len(inorder)):self.valToIndex[inorder[i]] = ireturn self.build(preorder, 0, len(preorder) - 1,inorder, 0, len(inorder) - 1)# 定义:中序遍历数组为 inorder[inStart..inEnd],# 后序遍历数组为 postorder[postStart..postEnd],# build 函数构造这个二叉树并返回该二叉树的根节点def build(self, preorder, preStart, preEnd, inorder, inStart, inEnd):if preStart > preEnd:return None# root 节点对应的值就是前序遍历数组的第一个元素rootVal = preorder[preStart]# rootVal 在中序遍历数组中的索引index = self.valToIndex[rootVal]leftSize = index - inStart# 先构造出当前根节点root = TreeNode(rootVal)# 递归构造左右子树root.left = self.build(preorder, preStart + 1, preStart + leftSize,inorder, inStart, index - 1)root.right = self.build(preorder, preStart + leftSize + 1, preEnd,inorder, index + 1, inEnd)return root106. 从中序与后序遍历序列构造二叉树 | 力扣 | LeetCode |
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1] 输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
基本思路
构造二叉树,第一件事一定是找根节点,然后想办法构造左右子树。
二叉树的后序和中序遍历结果的特点如下:
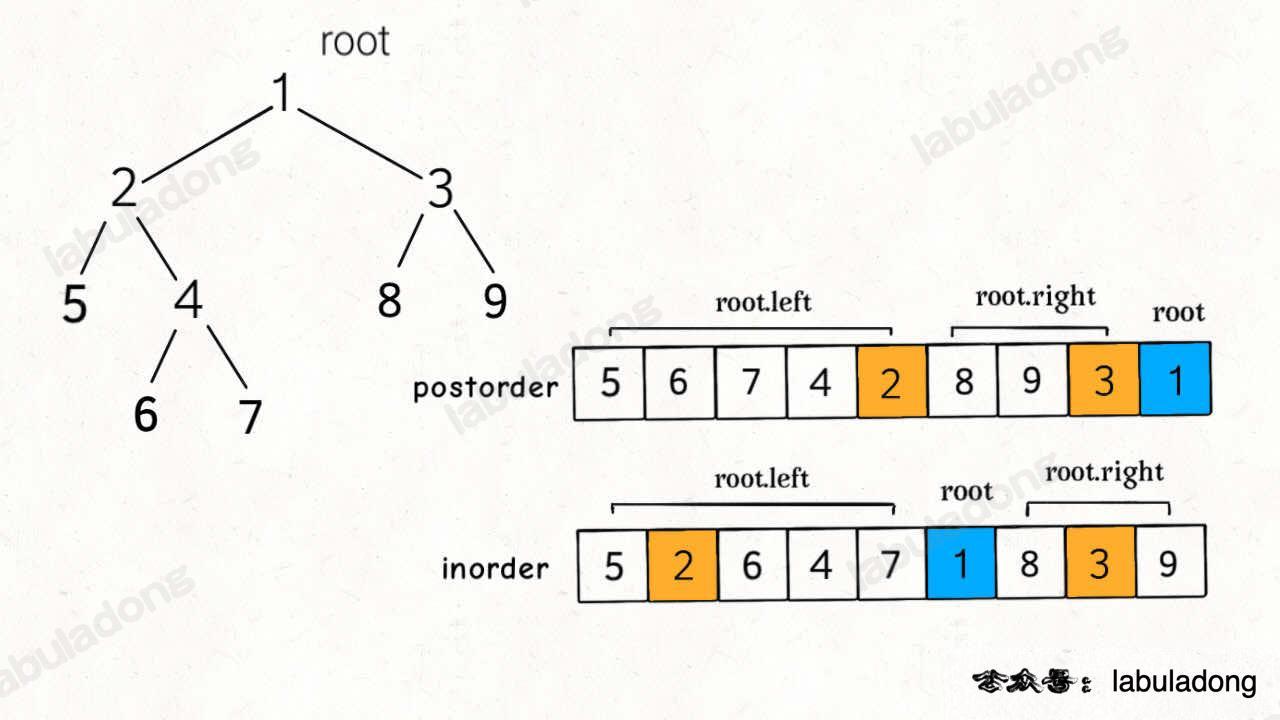
后序遍历结果最后一个就是根节点的值,然后再根据中序遍历结果确定左右子树的节点。
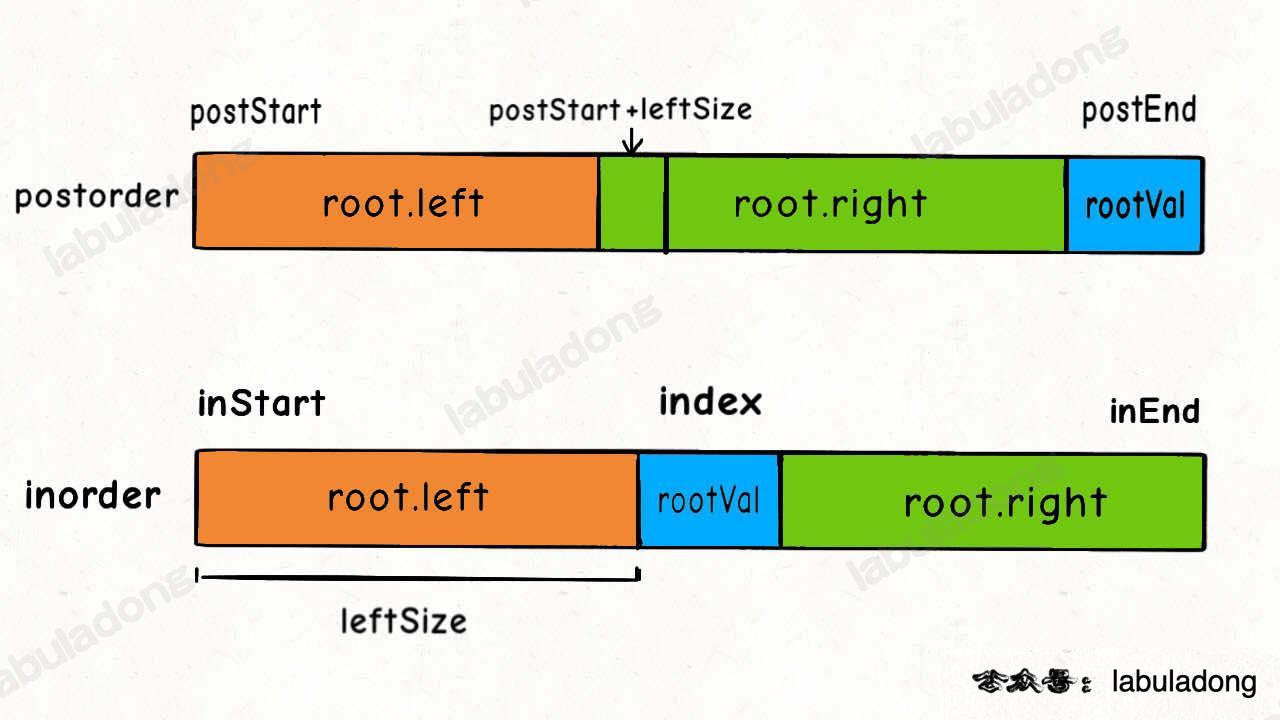
结合这个图看代码辅助理解。
详细题解
class Solution:# 存储 inorder 中值到索引的映射val_to_index = {}def buildTree(self, inorder, postorder):for i in range(len(inorder)):self.val_to_index[inorder[i]] = ireturn self.build(inorder, 0, len(inorder) - 1,postorder, 0, len(postorder) - 1)"""定义:中序遍历数组为 inorder[inStart..inEnd],后序遍历数组为 postorder[postStart..postEnd],构造这个二叉树并返回该二叉树的根节点"""def build(self, inorder, in_start, in_end,postorder, post_start, post_end):if in_start > in_end:return None# root 节点对应的值就是后序遍历数组的最后一个元素root_val = postorder[post_end]# rootVal 在中序遍历数组中的索引index = self.val_to_index[root_val]# 左子树的节点个数left_size = index - in_startroot = TreeNode(root_val) # 递归构造左右子树root.left = self.build(inorder, in_start, index - 1,postorder, post_start, post_start + left_size - 1)root.right = self.build(inorder, index + 1, in_end,postorder, post_start + left_size, post_end - 1)return root889. 根据前序和后序遍历构造二叉树 | 力扣 | LeetCode |
给定两个整数数组,preorder 和 postorder ,其中 preorder 是一个具有 无重复 值的二叉树的前序遍历,postorder 是同一棵树的后序遍历,重构并返回二叉树。
如果存在多个答案,您可以返回其中 任何 一个。
示例 1:

输入:preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1] 输出:[1,2,3,4,5,6,7]
示例 2:
输入: preorder = [1], postorder = [1] 输出: [1]
提示:
1 <= preorder.length <= 301 <= preorder[i] <= preorder.lengthpreorder中所有值都 不同postorder.length == preorder.length1 <= postorder[i] <= postorder.lengthpostorder中所有值都 不同- 保证
preorder和postorder是同一棵二叉树的前序遍历和后序遍历
基本思路
做这道题之前,建议你先看一下 二叉树心法(构造篇),做一下 105. 从前序与中序遍历序列构造二叉树(中等) 和 106. 从中序与后序遍历序列构造二叉树(中等) 这两道题。
这道题让用后序遍历和前序遍历结果还原二叉树,和前两道题有一个本质的区别:
通过前序中序,或者后序中序遍历结果可以确定一棵原始二叉树,但是通过前序后序遍历结果无法确定原始二叉树。题目也说了,如果有多种结果,你可以返回任意一种。
为什么呢?我们说过,构建二叉树的套路很简单,先找到根节点,然后找到并递归构造左右子树即可。
前两道题,可以通过前序或者后序遍历结果找到根节点,然后根据中序遍历结果确定左右子树。
这道题,你可以确定根节点,但是无法确切的知道左右子树有哪些节点。
举个例子,下面这两棵树结构不同,但是它们的前序遍历和后序遍历结果是相同的:
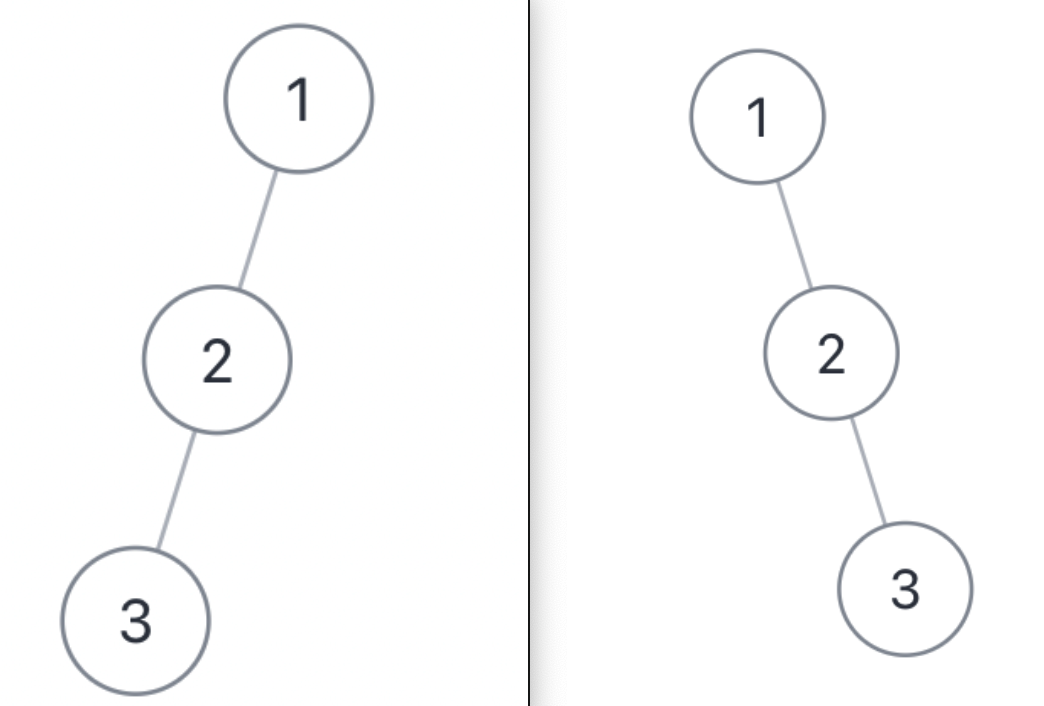
不过话说回来,用后序遍历和前序遍历结果还原二叉树,解法逻辑上和前两道题差别不大,也是通过控制左右子树的索引来构建:
1、首先把前序遍历结果的第一个元素或者后序遍历结果的最后一个元素确定为根节点的值。
2、然后把前序遍历结果的第二个元素作为左子树的根节点的值。
3、在后序遍历结果中寻找左子树根节点的值,从而确定了左子树的索引边界,进而确定右子树的索引边界,递归构造左右子树即可。
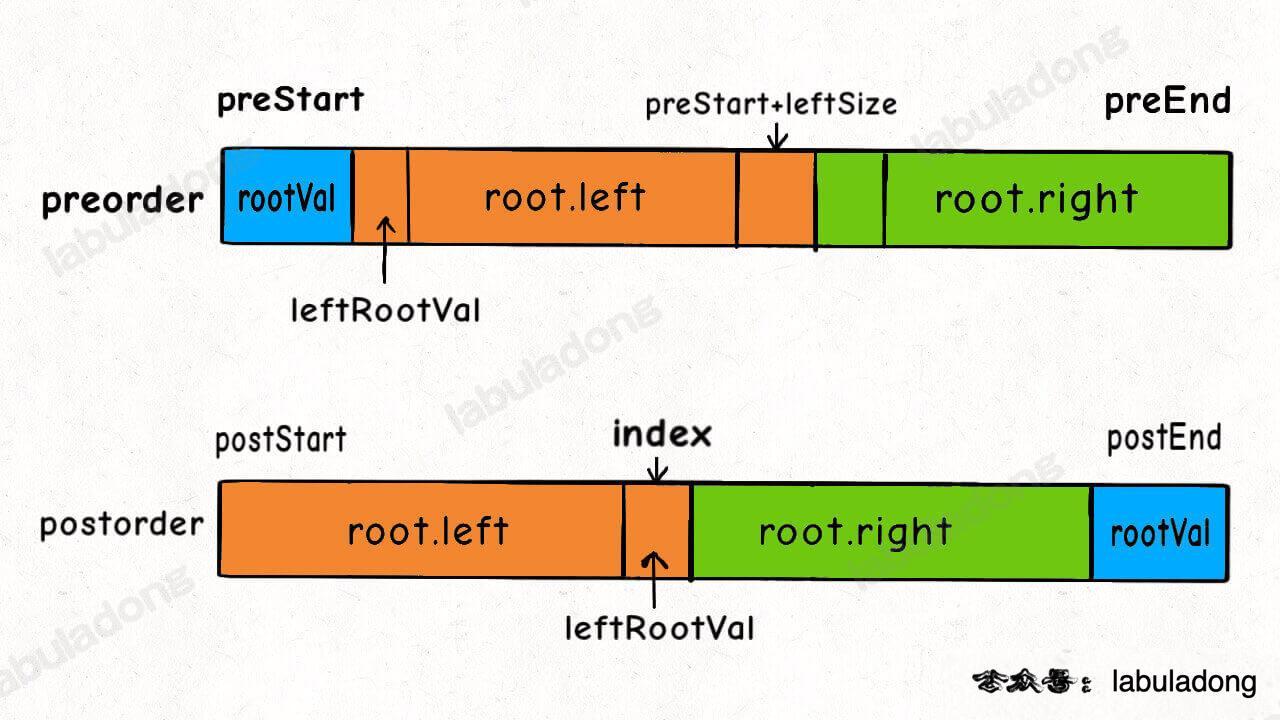
详细题解
class Solution:# 存储 postorder 中值到索引的映射def __init__(self):self.valToIndex = {}def constructFromPrePost(self, preorder, postorder):for i in range(len(postorder)):self.valToIndex[postorder[i]] = ireturn self.build(preorder, 0, len(preorder) - 1,postorder, 0, len(postorder) - 1)# 定义:根据 preorder[preStart..preEnd] 和 postorder[postStart..postEnd]# 构建二叉树,并返回根节点。def build(self, preorder, preStart, preEnd, postorder, postStart, postEnd):if preStart > preEnd:return Noneif preStart == preEnd:return TreeNode(preorder[preStart])# root 节点对应的值就是前序遍历数组的第一个元素rootVal = preorder[preStart]# root.left 的值是前序遍历第二个元素# 通过前序和后序遍历构造二叉树的关键在于通过左子树的根节点# 确定 preorder 和 postorder 中左右子树的元素区间leftRootVal = preorder[preStart + 1]# leftRootVal 在后序遍历数组中的索引index = self.valToIndex[leftRootVal]# 左子树的元素个数leftSize = index - postStart + 1# 先构造出当前根节点root = TreeNode(rootVal)# 递归构造左右子树# 根据左子树的根节点索引和元素个数推导左右子树的索引边界root.left = self.build(preorder, preStart + 1, preStart + leftSize,postorder, postStart, index)root.right = self.build(preorder, preStart + leftSize + 1, preEnd,postorder, index + 1, postEnd - 1)return root331. 验证二叉树的前序序列化 | 力扣 | LeetCode |
序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时,我们可以记录下这个节点的值。如果它是一个空节点,我们可以使用一个标记值记录,例如 #。
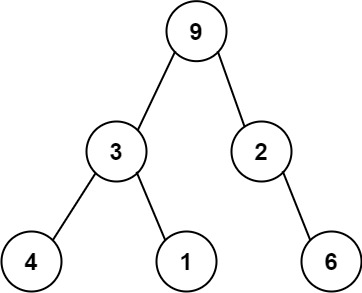
例如,上面的二叉树可以被序列化为字符串 "9,3,4,#,#,1,#,#,2,#,6,#,#",其中 # 代表一个空节点。
给定一串以逗号分隔的序列,验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。
保证 每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 '#' 。
你可以认为输入格式总是有效的
- 例如它永远不会包含两个连续的逗号,比如
"1,,3"。
注意:不允许重建树。
示例 1:
输入: preorder ="9,3,4,#,#,1,#,#,2,#,6,#,#"输出:true
示例 2:
输入: preorder ="1,#"输出:false
示例 3:
输入: preorder ="9,#,#,1"输出:false
提示
1 <= preorder.length <= 104preorder由以逗号“,”分隔的[0,100]范围内的整数和“#”组成
基本思路
首先,如果看过前文 手把手带你刷二叉树(序列化篇) 理解了前序遍历序列化和反序列化的原理,肯定可以通过改造反序列化函数 deserialize 来判断序列化的合法性。
另外还有一种更巧妙的解法,就是利用二叉树节点和边的关系。
每个非空的二叉树节点都会产生两条边,并消耗一条边;而每个空节点只会消耗一条边:
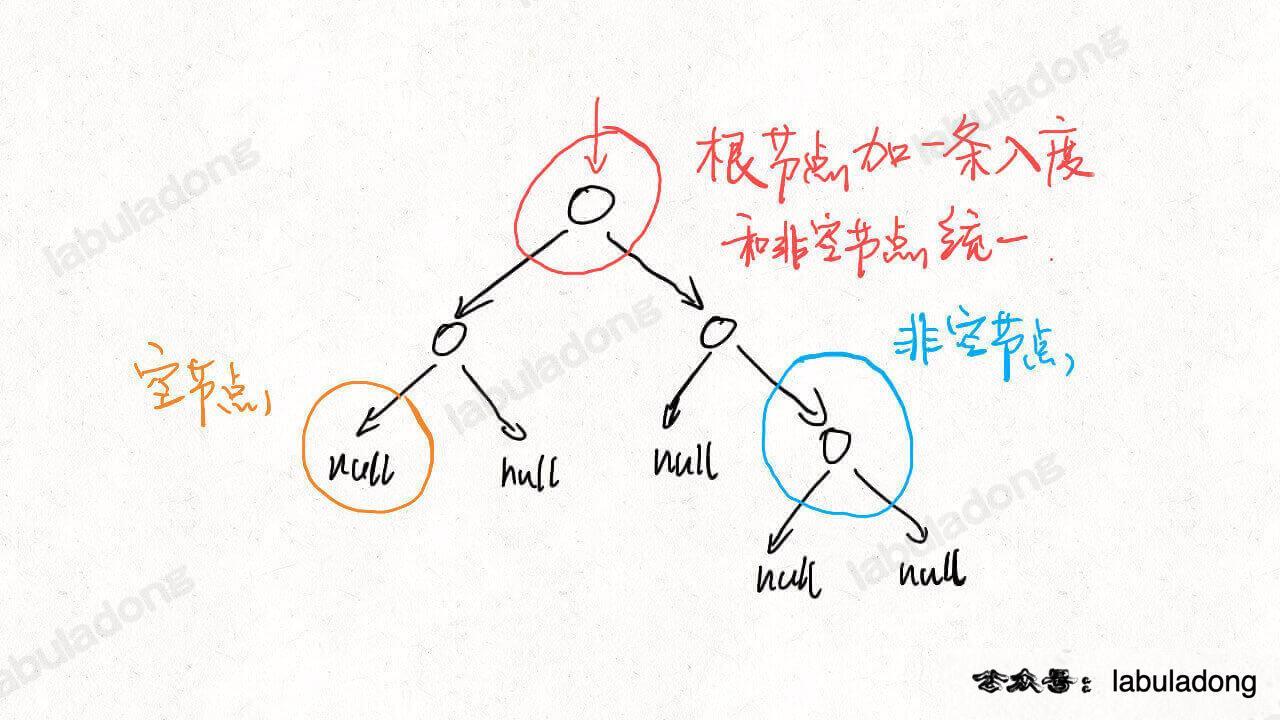
详细题解
class Solution:def isValidSerialization(self, preorder: str) -> bool:# 一条指向根节点的虚拟边edge = 1for node in preorder.split(","):# 任何时候,边数都不能小于 0if node == "#":# 空指针消耗一条空闲边edge -= 1if edge < 0:return Falseelse:# 非空节点消耗一条空闲边,增加两条空闲边edge -= 1if edge < 0:return Falseedge += 2# 最后不应该存在空闲边return edge == 0class Solution2:def isValidSerialization(self, preorder: str) -> bool:# 将字符串转化成列表nodes = list(preorder.split(","))return self.deserialize(nodes) and len(nodes) == 0# 改造后的前序遍历反序列化函数# 详细解析:https://labuladong.online/algo/data-structure/serialize-and-deserialize-binary-tree/def deserialize(self, nodes) -> bool:if not nodes:return False# ***** 前序遍历位置 *****# 列表最左侧就是根节点first = nodes.pop(0)if first == "#":return True# *********************return self.deserialize(nodes) and self.deserialize(nodes)654. 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:
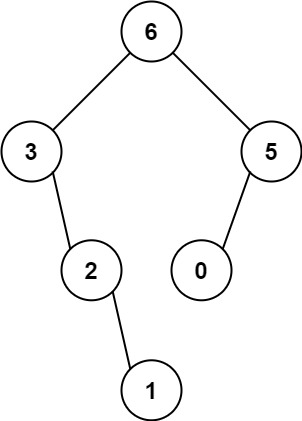
输入:nums = [3,2,1,6,0,5] 输出:[6,3,5,null,2,0,null,null,1] 解释:递归调用如下所示: - [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。- 空数组,无子节点。- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。- 空数组,无子节点。- 只有一个元素,所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。- 只有一个元素,所以子节点是一个值为 0 的节点。- 空数组,无子节点。
示例 2:
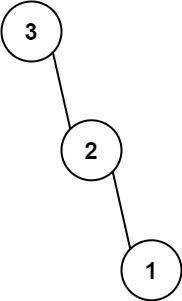
输入:nums = [3,2,1] 输出:[3,null,2,null,1]
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000nums中的所有整数 互不相同
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
做这道题之前,你一定要去做一下 654. 最大二叉树 这道题,知道了构建最大二叉树的逻辑就很容易解决这道题了。
新增的 val 是添加在原始数组的最后的,根据构建最大二叉树的逻辑,正常来说最后的这个值一定是在右子树的,可以对右子树递归调用 insertIntoMaxTree 插入进去。
但是一种特殊情况是 val 比原始数组中的所有元素都大,那么根据构建最大二叉树的逻辑,原来的这棵树应该成为 val 节点的左子树。
详细题解
class Solution:def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:def construct(left: int, right: int) -> Optional[TreeNode]:if left > right:return Nonebest = leftfor i in range(left + 1, right + 1):if nums[i] > nums[best]:best = inode = TreeNode(nums[best])node.left = construct(left, best - 1)node.right = construct(best + 1, right)return nodereturn construct(0, len(nums) - 1)
998. 最大二叉树 II | 力扣 | LeetCode |
最大树 定义:一棵树,并满足:其中每个节点的值都大于其子树中的任何其他值。
给你最大树的根节点 root 和一个整数 val 。
就像 之前的问题 那样,给定的树是利用 Construct(a) 例程从列表 a(root = Construct(a))递归地构建的:
- 如果
a为空,返回null。 - 否则,令
a[i]作为a的最大元素。创建一个值为a[i]的根节点root。 root的左子树将被构建为Construct([a[0], a[1], ..., a[i - 1]])。root的右子树将被构建为Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]])。- 返回
root。
请注意,题目没有直接给出 a ,只是给出一个根节点 root = Construct(a) 。
假设 b 是 a 的副本,并在末尾附加值 val。题目数据保证 b 中的值互不相同。
返回 Construct(b) 。
示例 1:
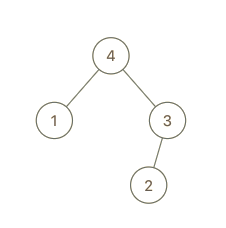
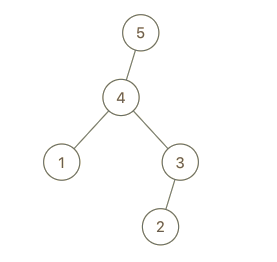
输入:root = [4,1,3,null,null,2], val = 5 输出:[5,4,null,1,3,null,null,2] 解释:a = [1,4,2,3], b = [1,4,2,3,5]
示例 2:
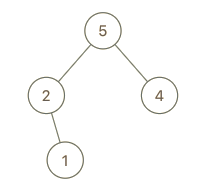

输入:root = [5,2,4,null,1], val = 3 输出:[5,2,4,null,1,null,3] 解释:a = [2,1,5,4], b = [2,1,5,4,3]
示例 3:
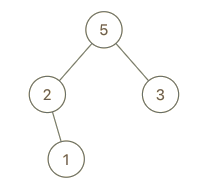
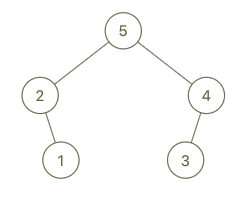
输入:root = [5,2,3,null,1], val = 4 输出:[5,2,4,null,1,3] 解释:a = [2,1,5,3], b = [2,1,5,3,4]
提示:
- 树中节点数目在范围
[1, 100]内 1 <= Node.val <= 100- 树中的所有值 互不相同
1 <= val <= 100
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
做这道题之前,你一定要去做一下 654. 最大二叉树 这道题,知道了构建最大二叉树的逻辑就很容易解决这道题了。
新增的 val 是添加在原始数组的最后的,根据构建最大二叉树的逻辑,正常来说最后的这个值一定是在右子树的,可以对右子树递归调用 insertIntoMaxTree 插入进去。
但是一种特殊情况是 val 比原始数组中的所有元素都大,那么根据构建最大二叉树的逻辑,原来的这棵树应该成为 val 节点的左子树。
详细题解
class Solution:def insertIntoMaxTree(self, root: TreeNode, val: int) -> TreeNode:if root is None:return TreeNode(val)if root.val < val:# 如果 val 是整棵树最大的,那么原来的这棵树应该是 val 节点的左子树,# 因为 val 节点是接在原始数组 a 的最后一个元素temp = rootroot = TreeNode(val)root.left = tempelse:# 如果 val 不是最大的,那么就应该在右子树上,# 因为 val 节点是接在原始数组 a 的最后一个元素root.right = self.insertIntoMaxTree(root.right, val)return root1110. 删点成林 | 力扣 | LeetCode |
给出二叉树的根节点 root,树上每个节点都有一个不同的值。
如果节点值在 to_delete 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。
返回森林中的每棵树。你可以按任意顺序组织答案。
示例 1:
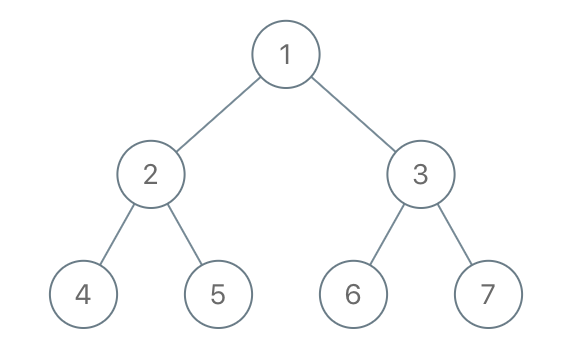
输入:root = [1,2,3,4,5,6,7], to_delete = [3,5] 输出:[[1,2,null,4],[6],[7]]
示例 2:
输入:root = [1,2,4,null,3], to_delete = [3] 输出:[[1,2,4]]
提示:
- 树中的节点数最大为
1000。 - 每个节点都有一个介于
1到1000之间的值,且各不相同。 to_delete.length <= 1000to_delete包含一些从1到1000、各不相同的值。
基本思路
前文 手把手刷二叉树总结篇 说过二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题需要用到「分解问题」的思维。
首先,如果在递归过程中修改二叉树结构,必须要让父节点接收递归函数的返回值,因为子树不管删成啥样,都要接到父节点上。
而且,手把手刷二叉树总结篇 说了可以通过函数参数传递父节点传递的数据,所以可以在前序位置判断是否得到了一个新的根节点。
详细题解
class Solution:def __init__(self):self.delSet = set()# 记录森林的根节点self.res = []def delNodes(self, root, to_delete):if root is None:return []for d in to_delete:self.delSet.add(d)self.doDelete(root, False)return self.res# 定义:输入一棵二叉树,删除 delSet 中的节点,返回删除完成后的根节点def doDelete(self, root, hasParent):if root is None:return None# 判断是否需要被删除deleted = root.val in self.delSetif not deleted and not hasParent:# 没有父节点且不需要被删除,就是一个新的根节点self.res.append(root)# 去左右子树进行删除root.left = self.doDelete(root.left, not deleted)root.right = self.doDelete(root.right, not deleted)# 如果需要被删除,返回 null 给父节点return None if deleted else root1485. 克隆含随机指针的二叉树 | 力扣 | LeetCode |
给你一个二叉树,树中每个节点都含有一个附加的随机指针,该指针可以指向树中的任何节点或者指向空(null)。
请返回该树的 深拷贝 。
该树的输入/输出形式与普通二叉树相同,每个节点都用 [val, random_index] 表示:
val:表示Node.val的整数random_index:随机指针指向的节点(在输入的树数组中)的下标;如果未指向任何节点,则为null。
该树以 Node 类的形式给出,而你需要以 NodeCopy 类的形式返回克隆得到的树。NodeCopy 类和Node 类定义一致。
示例 1:

输入:root = [[1,null],null,[4,3],[7,0]] 输出:[[1,null],null,[4,3],[7,0]] 解释:初始二叉树为 [1,null,4,7] 。 节点 1 的随机指针指向 null,所以表示为 [1, null] 。 节点 4 的随机指针指向 7,所以表示为 [4, 3] 其中 3 是树数组中节点 7 对应的下标。 节点 7 的随机指针指向 1,所以表示为 [7, 0] 其中 0 是树数组中节点 1 对应的下标。
示例 2:
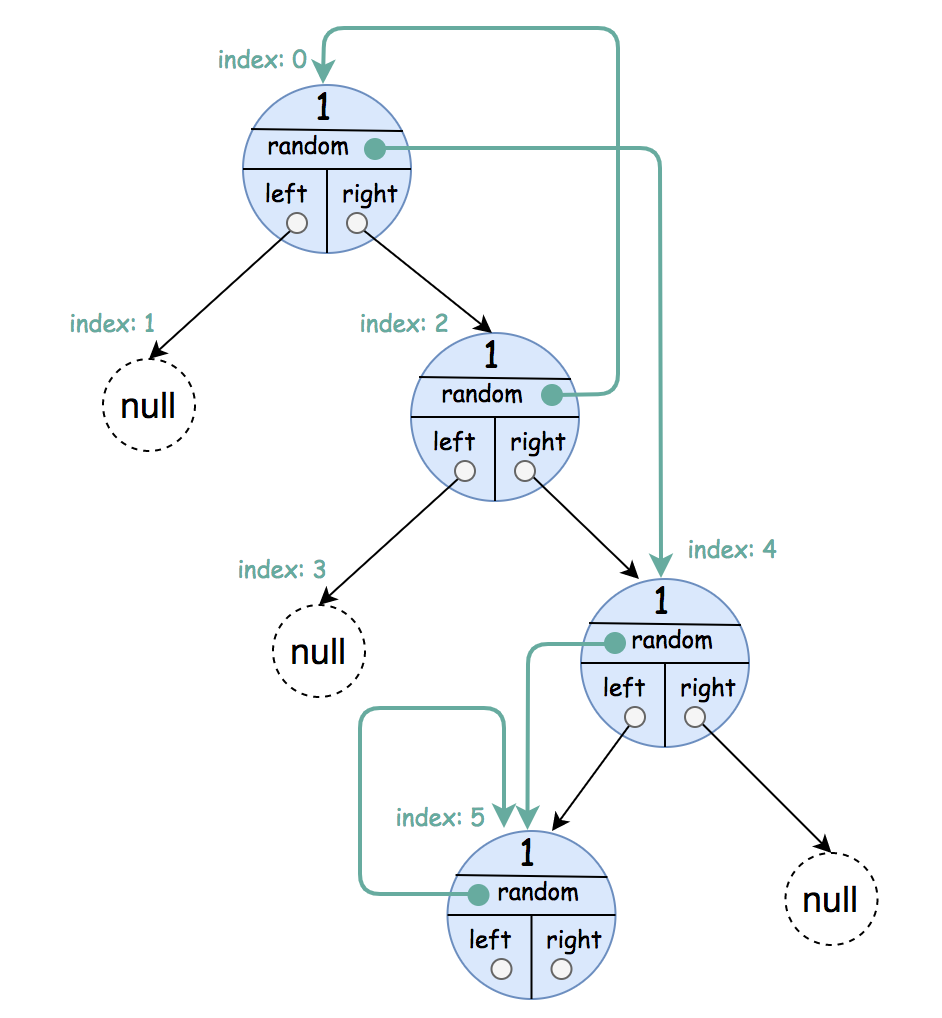
输入:root = [[1,4],null,[1,0],null,[1,5],[1,5]] 输出:[[1,4],null,[1,0],null,[1,5],[1,5]] 解释:节点的随机指针可以指向它自身。
示例 3:
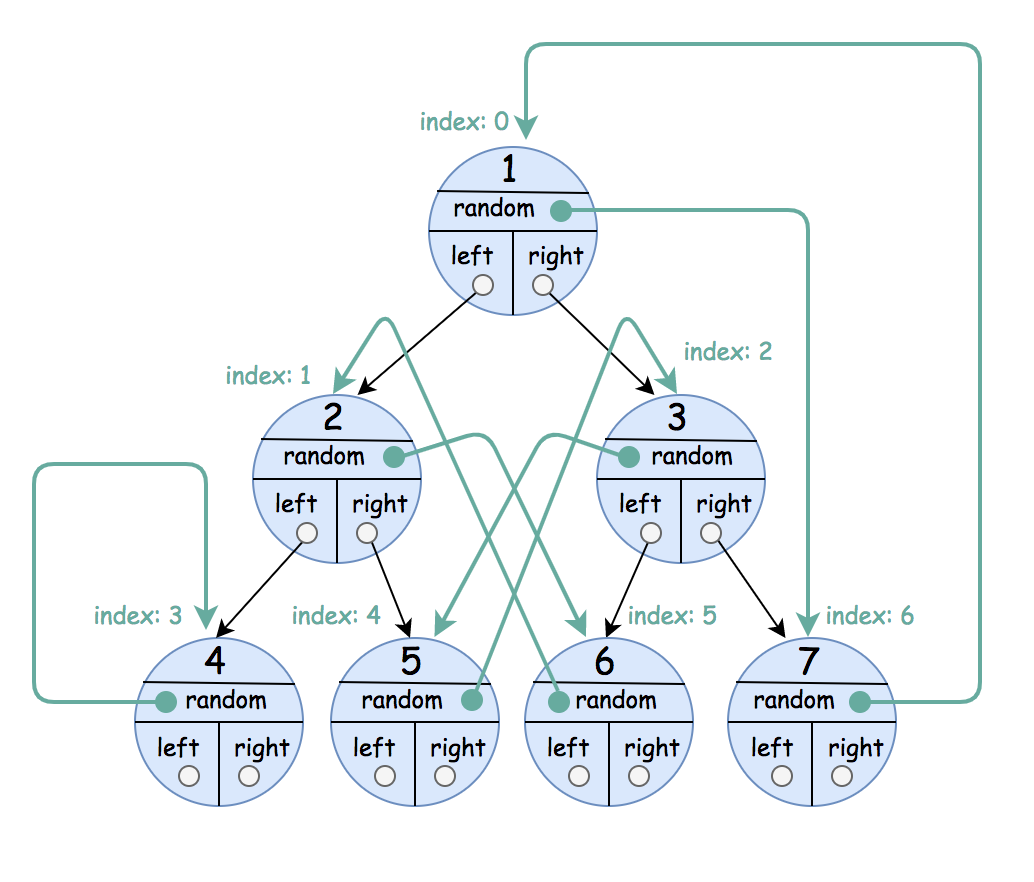
输入:root = [[1,6],[2,5],[3,4],[4,3],[5,2],[6,1],[7,0]] 输出:[[1,6],[2,5],[3,4],[4,3],[5,2],[6,1],[7,0]]
提示:
tree中节点数目范围是[0, 1000]- 每个节点的值的范围是
[1, 10^6]
基本思路
这道题和一般的二叉树构造问题思路是一样的,函数的定义就是复制二叉树并返回根节点,那么把根节点构造出来之后,递归调用子节点就行了,基本算法框架肯定是这样:
// 定义:输入一棵二叉树的根节点 root,复制这棵树并返回复制后的根节点
public NodeCopy copyRandomBinaryTree(Node root) {if (root == null) {return null;}NodeCopy rootCopy = new NodeCopy(root.val);// 根据函数定义递归构造三个子节点rootCopy.left = copyRandomBinaryTree(root.left);rootCopy.right = copyRandomBinaryTree(root.right);rootCopy.random = copyRandomBinaryTree(root.random);return rootCopy;
}但这道题的特殊之处在于 random 节点,可能指向任何节点,如果这个节点还没被构建出来,你应该把它 new 出来,但如果这个节点已经被构建出来了,你直接把 random 指针指向这个节点就行了。
想做到这一点也很简单,用一个 HashMap 存储原始节点到复制节点的映射就行了,这样就能知道哪些节点已经被构建出来了。
详细题解
class Solution:# 原始节点到复制节点的映射def __init__(self):self.node_to_copy = {}# 定义:输入一棵二叉树的根节点 root,复制这棵树并返回复制后的根节点def copyRandomBinaryTree(self, root):# 一个节点需要做的事情if root is None:return Noneif root in self.node_to_copy:return self.node_to_copy[root]# 在前序位置把自己存入 map 映射,之后如果有 random 指针# 指向自己的话可以直接从 map 里面拿出来root_copy = NodeCopy(root.val)self.node_to_copy[root] = root_copy# 根据函数定义递归构造三个子节点root_copy.left = self.copyRandomBinaryTree(root.left)root_copy.right = self.copyRandomBinaryTree(root.right)root_copy.random = self.copyRandomBinaryTree(root.random)return root_copy1660. 纠正二叉树 | 力扣 | LeetCode |
你有一棵二叉树,这棵二叉树有个小问题,其中有且只有一个无效节点,它的右子节点错误地指向了与其在同一层且在其右侧的一个其他节点。
给定一棵这样的问题二叉树的根节点 root ,将该无效节点及其所有子节点移除(除被错误指向的节点外),然后返回新二叉树的根结点。
自定义测试用例:
测试用例的输入由三行组成:
TreeNode rootint fromNode(在correctBinaryTree中不可见)int toNode(在correctBinaryTree中不可见)
当以 root 为根的二叉树被解析后,值为 fromNode 的节点 TreeNode 将其右子节点指向值为 toNode 的节点 TreeNode 。然后, root 传入 correctBinaryTree 的参数中。
示例 1:
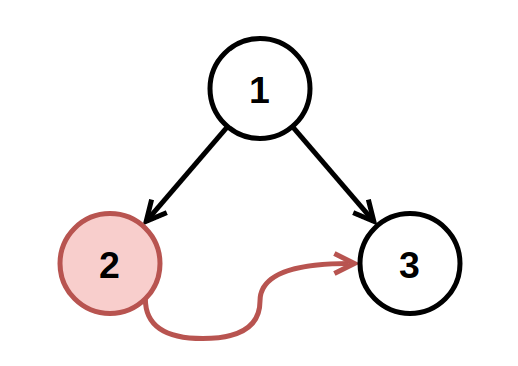
输入: root = [1,2,3], fromNode = 2, toNode = 3 输出: [1,null,3] 解释: 值为 2 的节点是无效的,所以移除之。
示例 2:
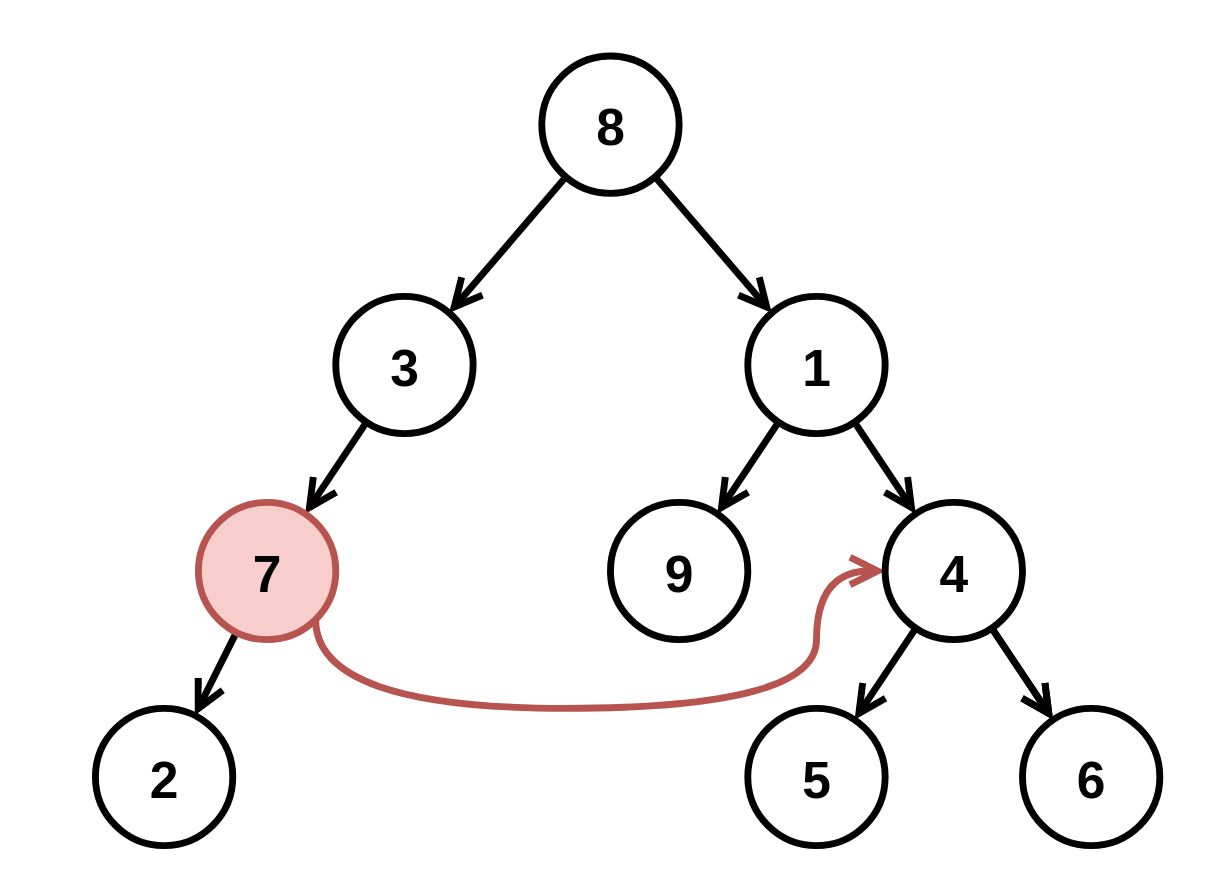
输入: root = [8,3,1,7,null,9,4,2,null,null,null,5,6], fromNode = 7, toNode = 4 输出: [8,3,1,null,null,9,4,null,null,5,6] 解释: 值为 7 的节点是无效的,所以移除这个节点及其子节点 2。
提示:
- 树中节点个数的范围是
[3, 104]。 -109 <= Node.val <= 109- 所有的
Node.val都是互不相同的。 fromNode != toNodefromNode和toNode将出现在树中的同一层。toNode在fromNode的右侧。fromNode.right在测试用例的树中建立后为null。
基本思路
这道题要求你熟悉如何构造二叉树,而且还要理解二叉树的遍历顺序。
如何知道一个节点 x 是「错误」节点?
需要要知道它的右子节点错误地指向同层右侧的一另一个节点。
那么如何让节点 x 知道自己错指了呢?
如果用层序遍历的方式应该比较容易想到解法,我们可以从右向左遍历每一行的节点并记录下来访问过的节点,如果你发现某个节点 x 的右子节点已经被访问过,那么这个节点 x 就是错误节点。
如果用递归遍历的方式,如何做到「从右向左」遍历每一行的节点呢?只要稍微改一下二叉树的遍历框架,先遍历右子树后遍历左子树,这样就是先遍历右侧节点后遍历左侧节点,也就相当于从右向左遍历了。
同理,遍历的时候我们同时记录已遍历的节点。这样 x 如果发现自己的右子节点已经被访问了,就说明 x 节点是「错误」的。具体思路见代码注释。
详细题解
class Solution:# 记录已访问过的节点visited = set()def correctBinaryTree(self, root: TreeNode) -> TreeNode:if root is None:return Noneif root.right is not None and root.right in self.visited:# 找到「无效节点」,删除整棵子树return Noneself.visited.add(root)# 要先遍历右子树,后遍历左子树root.right = self.correctBinaryTree(root.right)root.left = self.correctBinaryTree(root.left)return root相关文章:

【leetcode练习·二叉树】用「分解问题」思维解题 I
本文参考labuladong算法笔记[【强化练习】用「分解问题」思维解题 I | labuladong 的算法笔记] 105. 从前序与中序遍历序列构造二叉树 | 力扣 | LeetCode | 给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵…...

【gitlab-ce】各组件介绍
主要组件功能接介绍(chatgpt回答的) nginx:作为Web服务器和反向代理,用于访问GitLab的Web界面。可以关闭,但会导致无法通过Web界面访问GitLab。prometheus_monitoring:提供监控和报警功能,收集和…...

PostgreSQL分区表:基础语法与运维实践
引言 简介:什么是数据库分区 数据库分区是一种将大型表物理上分割成多个较小的部分的技术。每个部分称为一个分区,这些分区可以分布在不同的存储设备上,以提高查询性能和管理效率。 为什么使用分区表 提高查询性能:通过减少需…...

Docker入门系列——DockerFile的使用
前面了解了Docker的基本概念,今天来认识一下DockerFile。 Dockerfile 是一个文本文件,包含一系列指令来组装 Docker 镜像。每个指令执行一个特定动作,例如安装包、复制文件或定义启动命令。正确使用 Dockerfile 指令对于构建高效容器至关重要…...
数据集平台分享
Kaggle: Your Machine Learning and Data Science CommunityKaggle is the world’s largest data science community with powerful tools and resources to help you achieve your data science goals.https://www.kaggle.com/Kaggle 包含非常丰富的数据集和代码,…...

去地面算法——depth_clustering算法调试(1)
1 源码下载 论文: 《2016-Fast Range Image-Based Segmentation of Sparse 3D Laser Scans for Online Operation》 《2017-Efficient Online Segmentation for Sparse 3D Laser Scans》 代码:git链接 2 问题记录 2.1 无法找到qt问题 问题截图&…...

设计模式-七个基本原则之一-单一职责原则 + SpringBoot案例
单一职责原理:(SRP) 面向对象七个基本原则之一 清晰的职责:每个类应该有一个明确的职责,避免将多个责任混合在一起。降低耦合:通过将不同的职责分开,可以降低类之间的耦合度,提高系统的灵活性。易于维护:当…...

HWA高速辅助驾驶系统组成及功能场景
HWA最基本功能包括智能跟车、拨杆变道、压速变道、车道居中保持等功能,有效减轻驾驶疲劳。随着智能驾驶不断走向成熟,HWA升级到高速自动驾驶HWP,可实现智能避让汇入口、智能避让大车、分心/疲劳监测、智能进出匝道、智能判别易混分叉路口、智…...

SpringMVC学习笔记(一)
一、SpringMVC的基本概念 (一)三层架构和MVC 1、三层架构概述 我们的开发架构一般都是基于两种形式,一种是 C/S 架构,也就是客户端/服务器,另一种是 B/S 架构,也就是浏览器服务器。在 JavaEE 开发中&…...

kaggle 如何利用API下载数据集
首先 上传kaggle官网生成得 API 密钥: kaggle.json 文件。放到该代码同目录下,再运行一下代码。 注: 只需要修改下载竞赛数据集,就可以选择你的指定数据集。 jupyter文件运行 #首先 上传 kaggle.json 文件并设置 API 密钥 #再…...

第一个 Flutter 项目(1)共46节
前端开发工具vs code,安装Flutter sdk,如果你的下载速度比较慢,可以选择这个😄 flutter sdk 解压码:stwq 配置可以看这Flutter 新建工程一直等待 解决办法-CSDN博客 如果你是新的 Flutter 开发者,我们建…...

学术论文写作丨机器学习与深度学习
目录 第一章、ChatGPT-4o使用方法与技巧 第二章、ChatGPT-4o辅助文献检索、总结与分析 第三章、ChatGPT-4o辅助学术论文选题、创新点挖掘与实验方案设计 第四章、ChatGPT-4o辅助学术论文开题与大纲生成 第五章、ChatGPT-4o辅助学术论文写作马拉松活动介绍 第六章、ChatGP…...

导-4涉及的知识点
除了本课题,3D结构几何修复领域还有以下一些值得关注的研究: 1. **Poisson图像编辑**: 成功地将给定的纹理块融合到可能完全不同的背景图像上。 2. **张量投票(TV)框架**: - 讨论了使用张量投票框架进…...

从0开始深度学习(28)——序列模型
序列模型是指一类特别设计来处理序列数据的神经网络模型。序列数据指的是数据中的每个元素都有先后顺序,比如时间序列数据(股票价格、天气变化等)、自然语言文本(句子中的单词顺序)、语音信号等。 1 统计工具 前面介绍…...

vue2使用 <component> 标签动态渲染不同的表单组件
在后台管理系统中,涉及到大量表单信息的修改和新增。现在想对模板中代码做一些简单的优化。 1. 使用 v-for 循环简化表单项 可以将表单项的定义提取到一个数组中,然后使用 v-for 循环来生成这些表单项。这将减少重复代码,提高可维护性。 2…...

C#实现在windows上实现指定句柄窗口的指定窗口坐标点击鼠标左键和右键的详细情况
在Windows编程中,有时我们需要对特定窗口进行操作,比如模拟鼠标点击。这在自动化测试、脚本编写或某些特定应用程序的开发中尤为常见。本文将深入探讨如何在C#中实现对指定句柄窗口进行鼠标点击操作,包括左键和右键点击。我们会从理论背景开始…...

探索Python自动化新境界:Invoke库的神秘面纱
文章目录 **探索Python自动化新境界:Invoke库的神秘面纱**第一部分:背景介绍第二部分:Invoke库是什么?第三部分:如何安装Invoke库?第四部分:Invoke库函数使用方法1. 定义任务2. 执行任务3. 任务…...

CSS样式实现3D效果
CSS 3D效果是通过CSS3中的transform和perspective等属性来实现的。这些属性允许你创建具有深度感和三维外观的网页元素。以下是一些常见的CSS 3D效果及其实现方法: 1. 3D旋转(Rotate) 使用transform: rotateX(), rotateY(), rotateZ()来分别…...

华为eNSP:MSTP
一、什么是MSTP? 1、MSTP是IEEE 802.1S中定义的生成树协议,MSTP兼容STP和RSTP,既可以快速收敛,也提供了数据转发的多个冗余路径,在数据转发过程中实现VLAN数据的负载均衡。 2、MSTP可以将一个或多个VLAN映射到一个Inst…...

modbus协议 Mthings模拟器使用
进制转换 HEX 16进制 (0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F表示0-15) dec 10进制 n(16进制) -> 10 abcd.efg(n) d*n^0 c*n^1 b*n^2 a*n^3 e*n^-1 f*n^-2 g*n^-3(10) 10 -> n(16进制) Modbus基础概念 高位为NUM_H&…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
