深入解析贪心算法及其应用实例
标题:深入解析贪心算法及其应用实例
一、引言
贪心算法(Greedy Algorithm)是一类简单、直观的算法设计策略,广泛应用于优化问题中。其基本思想是每一步都选择当前状态下最优的选择,即在每一步做出局部最优的决策,期望通过这些局部最优选择的叠加,最终达到全局最优解。贪心算法因其实现简单、效率高而广泛应用于许多经典问题的求解中。
本篇文章将深入探讨贪心算法的基本原理、常见应用及其优势与局限,并通过具体实例来帮助读者更好地理解贪心算法的实际应用场景。
二、贪心算法的基本原理
贪心算法通过在每一步选择中都采取当前看来最优的选择,从而希望能够得到全局最优解。贪心算法的核心思想可以总结为以下几个步骤:
- 选择:在当前状态下选择一个看似最优的解。
- 决策:做出该选择后,更新问题的状态,进入下一阶段。
- 判断:判断是否已经找到问题的解,如果已经达到目标则结束算法;如果没有,则继续进行选择和决策。
贪心算法并不总是能得到全局最优解,尤其是在复杂问题中。其是否能够得到全局最优解,通常依赖于问题本身是否满足贪心选择性质和最优子结构两个条件:
- 贪心选择性质:通过选择局部最优解,能够达到全局最优解。
- 最优子结构:问题的最优解包含子问题的最优解。
三、贪心算法的特点
贪心算法与动态规划、回溯算法等其他算法设计方法相比,具有一些独特的特点:
- 简单性:贪心算法通常比其他算法更简单,易于实现和理解。
- 效率高:贪心算法每次都进行一次简单的选择和决策,通常时间复杂度较低,适合处理规模较大的问题。
- 局部最优性:贪心算法每次都选择局部最优解,而不考虑全局情况,这也使得它的解并不一定是全局最优解。
四、贪心算法的应用
贪心算法被广泛应用于许多领域,特别是在解决优化问题时。以下是几个经典的贪心算法应用实例。
1. 活动选择问题
活动选择问题(Activity Selection Problem)是一个典型的贪心算法问题,其目的是在给定的多个活动中,选择出最多的互不重叠的活动。活动的开始和结束时间已知,贪心算法通过选择最早结束的活动,能够保证剩余时间的活动选择空间最大,从而达到最大活动数量。
问题描述:
给定一组活动,每个活动都有开始时间和结束时间。要求选择最多的活动,使得它们之间没有时间冲突。
贪心选择策略:
- 每次选择结束时间最早的活动。
伪代码:
def activity_selection(start, finish):n = len(start)selected = []# 按结束时间排序activities = sorted(zip(start, finish), key=lambda x: x[1])# 第一个活动总是选择selected.append(activities[0])last_finish_time = activities[0][1]for i in range(1, n):if activities[i][0] >= last_finish_time: # 当前活动的开始时间大于或等于上一活动的结束时间selected.append(activities[i])last_finish_time = activities[i][1]return selected
通过贪心策略,活动选择问题能够有效地求解,并且算法的时间复杂度为O(n log n),其中n是活动的数量。
2. 零钱兑换问题
零钱兑换问题(Coin Change Problem)也是贪心算法的一种经典应用。给定一组硬币面额,要求用尽量少的硬币组合出某个金额。
问题描述:
给定一个金额和一组硬币面额,要求用最少的硬币组合来凑出该金额。
贪心选择策略:
- 每次选择面额最大的硬币,直到凑齐目标金额。
伪代码:
def coin_change(coins, amount):coins.sort(reverse=True) # 按从大到小排序count = 0for coin in coins:if amount >= coin:count += amount // coin # 使用尽量多的当前面额硬币amount %= coinif amount == 0:breakreturn count if amount == 0 else -1 # 如果金额无法凑齐,返回-1
虽然贪心算法对某些特定面额组合(如1、5、10、25等)能够得到最优解,但在其他面额组合下,贪心算法可能不能得到最优解。比如,对于面额为{1, 3, 4},如果目标金额是6,贪心算法选择的硬币组合是{4, 1, 1},而最优解应该是{3, 3}。
3. 哈夫曼编码
哈夫曼编码(Huffman Coding)是用于数据压缩的一种算法,其核心思想是通过构造最优的二叉树来实现字符的最优编码,从而减少数据传输所需要的空间。哈夫曼编码是典型的贪心算法应用。
问题描述:
给定一组字符及其频率,要求构造一个二叉树,使得频率较高的字符使用较短的编码,频率较低的字符使用较长的编码,从而达到数据压缩的目的。
贪心选择策略:
- 每次选择频率最小的两个节点进行合并,直到所有节点都合并成一棵树。
伪代码:
import heapqdef huffman_encoding(freq):heap = [[weight, [char, ""]] for char, weight in freq.items()]heapq.heapify(heap) # 构造最小堆while len(heap) > 1:lo = heapq.heappop(heap)hi = heapq.heappop(heap)for pair in lo[1:]:pair[1] = '0' + pair[1]for pair in hi[1:]:pair[1] = '1' + pair[1]heapq.heappush(heap, [lo[0] + hi[0]] + lo[1:] + hi[1:])return sorted(heap[0][1:], key=lambda p: (len(p[-1]), p))
在这个算法中,最小堆(优先队列)用于存储并不断选择频率最小的两个节点进行合并,直到所有节点被合并为一棵哈夫曼树。
五、贪心算法的局限性
尽管贪心算法在许多问题中表现出色,但它也有其局限性,特别是在以下情况下:
-
不一定能得到全局最优解:贪心算法的决策是基于当前局部最优解的,可能无法得到全局最优解。某些问题需要全局的信息来做出最优决策。
-
需要问题满足贪心选择性质和最优子结构:并不是所有问题都能够通过贪心算法得到最优解。要确保贪心算法能够正确工作,问题必须满足贪心选择性质和最优子结构。
六、总结
贪心算法是一种简单高效的算法设计策略,广泛应用于许多优化问题中。通过每次选择局部最优解,贪心算法能够在许多场景中提供有效的近似解。然而,贪心算法并不适用于所有问题,它只适用于那些满足贪心选择性质和最优子结构的问题。在实际应用中,我们需要根据问题的具体性质来判断是否采用贪心算法,并且需要根据问题的规模和复杂度选择合适的算法策略。
相关文章:

深入解析贪心算法及其应用实例
标题:深入解析贪心算法及其应用实例 一、引言 贪心算法(Greedy Algorithm)是一类简单、直观的算法设计策略,广泛应用于优化问题中。其基本思想是每一步都选择当前状态下最优的选择,即在每一步做出局部最优的决策&…...

电子工牌独立双通道定向拾音方案(有视频演示)
现在一些行业的客服人员在面对客户都要求使用电子工牌分别记录客服和顾客的声音,我们利用双麦克风阵列双波束拾音的方案设计了一个电子工牌方案.可以有效分别记录客服和顾客的声音. 方案思路: 我们采用了一个双麦阵列波束拾音的模块A-59,此模块可以利用2个麦克风组成阵列进行双…...
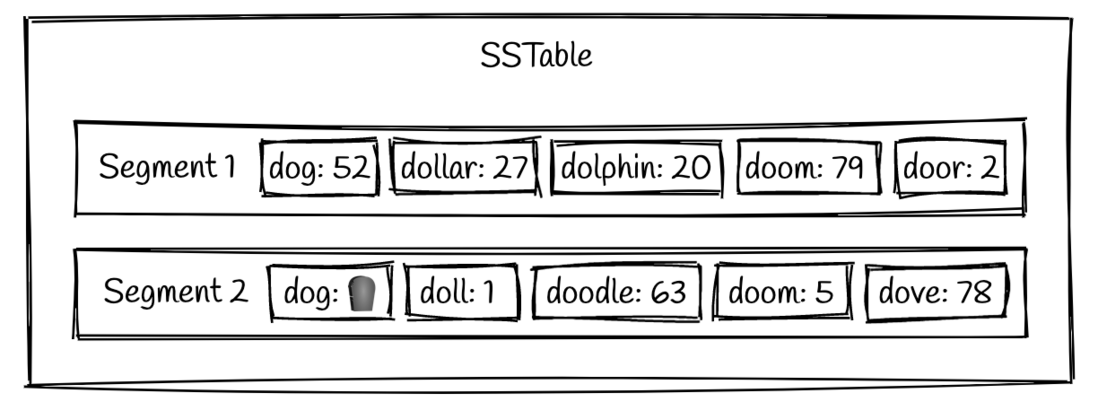
举例理解LSM-Tree,LSM-Tree和B+Tree的比较
写操作 write1:WAL 把操作同步到磁盘中WAL做备份(追加写、性能极高) write2:Memtable 完成WAL后将(k,v)数据写入内存中的Memtable,Memtable的数据结构一般是跳表或者红黑树 内存内采用这种数据结构一方面支持内存…...

React Native 全栈开发实战班 - 核心组件与导航
在 React Native 中,组件是构建用户界面的基本单元。React Native 提供了丰富的内置组件,涵盖了从基础布局到复杂交互的各种需求。本章节将详细介绍常用的内置组件,并重点讲解列表与滚动视图的使用。 1. 常用内置组件详解 React Native 提供…...

Leecode热题100-35.搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 示例 1: 输入: nums [1,3,5,6], target 5 输出: 2示例 2: 输入:…...

密码学知识点整理二:常见的加密算法
常用的加密算法包括对称加密算法、非对称加密算法和散列算法。 对称加密算法 AES:高级加密标准,是目前使用最广泛的对称加密算法之一,支持多种密钥长度(128位、192位、256位),安全性高,加密效率…...
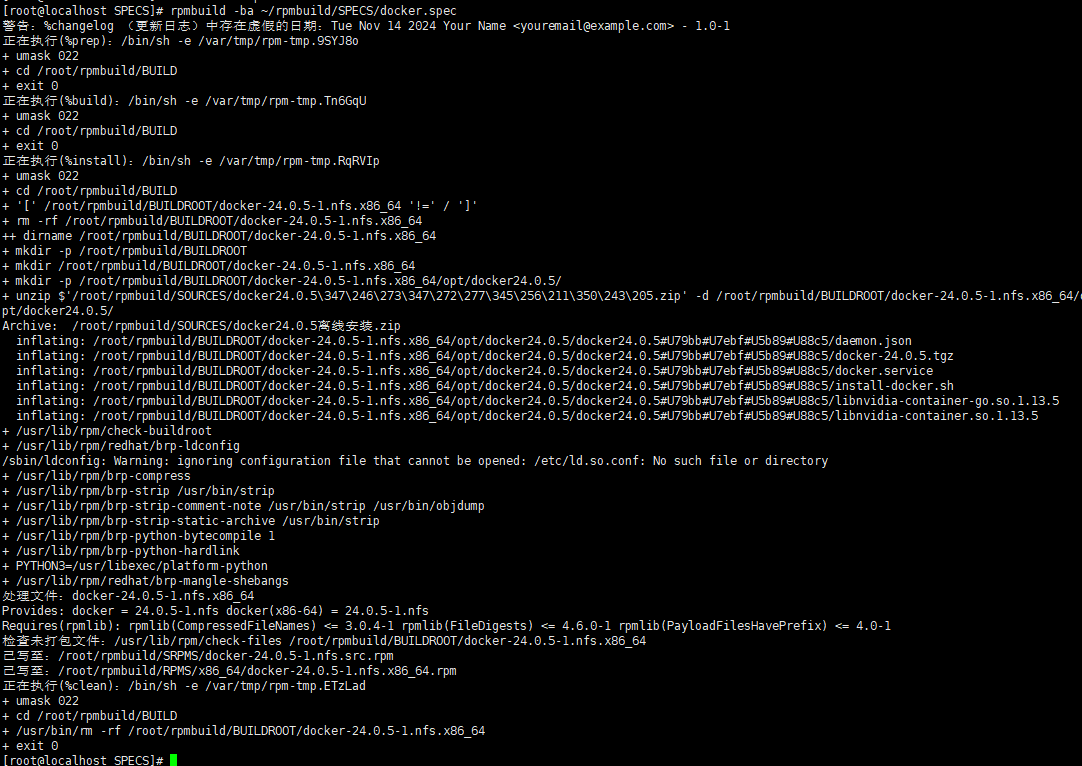
Linux如何将文件或目录打成rpm包?-- rpmbuild打包详解
👨🎓博主简介 🏅CSDN博客专家 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入!…...

RabbitMQ-死信队列(golang)
1、概念 死信(Dead Letter),字面上可以理解为未被消费者成功消费的信息,正常来说,生产者将消息放入到队列中,消费者从队列获取消息,并进行处理,但是由于某种原因,队列中的…...

爬虫开发工具与环境搭建——环境配置
第二章:爬虫开发工具与环境搭建 第二节:环境配置 在进行爬虫开发之前,首先需要配置好开发环境。一个良好的开发环境不仅能提高开发效率,还能避免因环境不一致带来的问题。以下是环境配置的详细步骤,涵盖了Python开发…...

15.UE5等级、经验、血条,魔法恢复和消耗制作
2-17 等级、经验、血条、魔法消耗_哔哩哔哩_bilibili 目录 1.制作UI,等级,经验,血条 2.为属性面板绑定角色真实的属性,实现动态更新 3.魔法的消耗和恢复 1.制作UI,等级,经验,血条 创建控…...

【Homework】【5】Learning resources for DQ Robotics in MATLAB
Lesson 5 代码-TwoDofPlanarRobot.m 表示一个 2 自由度平面机器人。该类包含构造函数、计算正向运动学模型的函数、计算平移雅可比矩阵的函数,以及在二维空间中绘制机器人的函数。 classdef TwoDofPlanarRobot%TwoDofPlanarRobot - 表示一个 2 自由度平面机器人类…...

vue3中 ref和reactive的区别
ref的主要作用 ref 函数接受的参数数据类型可以是原始数据类型也可以是引用数据类型。在模板中使用 ref 时,我们不需要加 .value,因为当 ref 在模板中作为顶层属性被访问时,它们会被自动解包, <p>count: {{ count }}</…...

第十四章 Spring之假如让你来写AOP——雏形篇
Spring源码阅读目录 第一部分——IOC篇 第一章 Spring之最熟悉的陌生人——IOC 第二章 Spring之假如让你来写IOC容器——加载资源篇 第三章 Spring之假如让你来写IOC容器——解析配置文件篇 第四章 Spring之假如让你来写IOC容器——XML配置文件篇 第五章 Spring之假如让你来写…...

群控系统服务端开发模式-应用开发-前端个人资料开发
一、总结 其实程序开发到现在,简单的后端框架就只剩下获取登录账号信息及获取登录账号菜单这两个功能咯。详细见下图: 1、未登录时总业务流程图 2、登录后总业务流程图 二、获取登录账号信息对接 在根目录下src文件夹下store文件夹下modules文件夹下的us…...

动态规划技巧点
动规五部曲(来自b站卡哥):1、确定DP数组中i、j…的含义。2、确定DP推导式。3、DP数组初始化。4、DP数组遍历顺序。5、DP数组打印校验。 父问题、子问题有些许区别:LeetCode343.整数拆分 今天在哔哩哔哩上刷到了一个非常有意思的l…...

深度学习之pytorch常见的学习率绘制
文章目录 0. Scope1. StepLR2. MultiStepLR3. ExponentialLR4. CosineAnnealingLR5. ReduceLROnPlateau6. CyclicLR7. OneCycleLR小结参考文献 https://blog.csdn.net/coldasice342/article/details/143435848 0. Scope 在深度学习中,学习率(Learning R…...
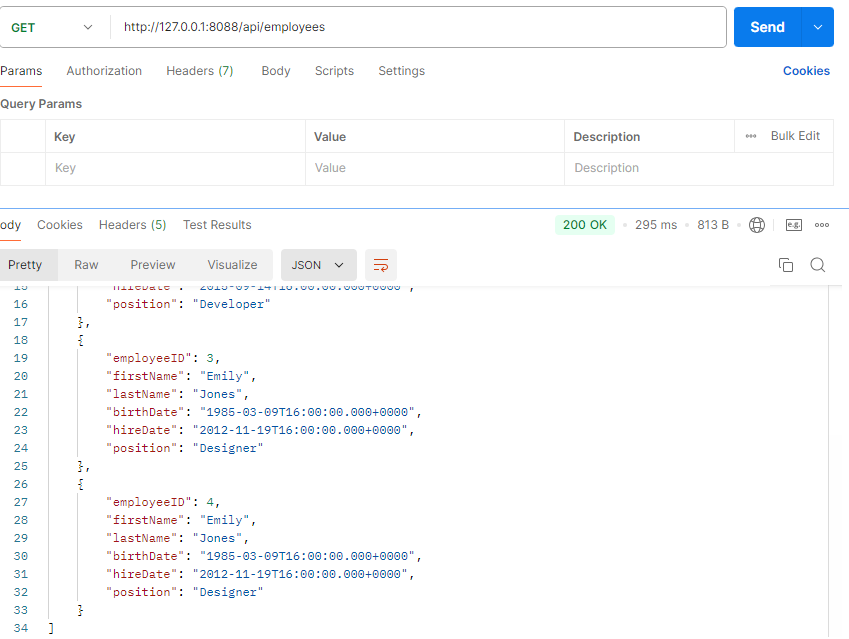
Spring Boot集成SQL Server快速入门Demo
1.什么是SQL Server? SQL Server是由Microsoft开发和推广的以客户/服务器(c/s)模式访问、使用Transact-SQL语言的关系数据库管理系统(DBMS),它最初是由Microsoft、Sybase和Ashton-Tate三家公司共同开发的&…...
低代码牵手 AI 接口:开启智能化开发新征程
一、低代码与 AI 接口的结合趋势 低代码开发平台近年来在软件开发领域迅速崛起。随着企业数字化转型的需求不断增长,低代码开发平台以其快速构建应用程序的优势,满足了企业对高效开发的需求。例如,启效云低代码平台通过范式化和高颗粒度的可配…...

【已解决】git push一直提示输入用户名及密码、fatal: Could not read from remote repository的问题
问题描述: 在实操中,git push代码到github上一直提示输入用户名及密码,并且跳出的输入框输入用户名和密码后,报错找不到远程仓库 实际解决中,发现我环境有两个问题解决: git push一直提示输入用户名及密码…...

python语言基础-4 常用模块-4.13 其他模块
声明:本内容非盈利性质,也不支持任何组织或个人将其用作盈利用途。本内容来源于参考书或网站,会尽量附上原文链接,并鼓励大家看原文。侵删。 4.13 其他模块 除此之外python中还有大量的功能模块,如: pill…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
