图论-代码随想录刷题记录[JAVA]
文章目录
- 前言
- 深度优先搜索理论基础
- 所有可达路径
- 岛屿数量
- 岛屿最大面积
- 孤岛的总面积
- 沉默孤岛
- Floyd 算法
- dijkstra(朴素版)
- 最小生成树之prim
- kruskal算法
前言
新手小白记录第一次刷代码随想录
1.自用 抽取精简的解题思路 方便复盘
2.代码尽量多加注释
3.记录踩坑
4.边刷边记录,更有成就感!
5.解题思路绝大部分来自代码随想录【仅自用 无商用!!!】
深度优先搜索理论基础
代码框架
void dfs(参数) {if (终止条件) {存放结果;return;}for (选择:本节点所连接的其他节点) {处理节点;dfs(图,选择的节点); // 递归回溯,撤销处理结果}
}
所有可达路径
【题目描述】
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
【输入描述】
第一行包含两个整数 N,M,表示图中拥有 N 个节点,M 条边
后续 M 行,每行包含两个整数 s 和 t,表示图中的 s 节点与 t 节点中有一条路径
【输出描述】
输出所有的可达路径,路径中所有节点的后面跟一个空格,每条路径独占一行,存在多条路径,路径输出的顺序可任意。
如果不存在任何一条路径,则输出 -1。
注意输出的序列中,最后一个节点后面没有空格! 例如正确的答案是 1 3 5,而不是 1 3 5, 5后面没有空格!
【输入示例】
5 5
1 3
3 5
1 2
2 4
4 5
【输出示例】
1 3 5
1 2 4 5
邻接矩阵
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;public class Main {static List<List<Integer>> result = new ArrayList<>(); // 收集符合条件的路径static List<Integer> path = new ArrayList<>(); // 1节点到终点的路径public static void dfs(int[][] graph, int x, int n) {// 当前遍历的节点x 到达节点nif (x == n) { // 找到符合条件的一条路径result.add(new ArrayList<>(path));return;}for (int i = 1; i <= n; i++) { // 遍历节点x链接的所有节点if (graph[x][i] == 1) { // 找到 x链接的节点path.add(i); // 遍历到的节点加入到路径中来dfs(graph, i, n); // 进入下一层递归path.remove(path.size() - 1); // 回溯,撤销本节点}}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 节点编号从1到n,所以申请 n+1 这么大的数组int[][] graph = new int[n + 1][n + 1];for (int i = 0; i < m; i++) {int s = scanner.nextInt();int t = scanner.nextInt();// 使用邻接矩阵表示无向图,1 表示 s 与 t 是相连的graph[s][t] = 1;}path.add(1); // 无论什么路径已经是从1节点出发dfs(graph, 1, n); // 开始遍历// 输出结果if (result.isEmpty()) System.out.println(-1);for (List<Integer> pa : result) {for (int i = 0; i < pa.size() - 1; i++) {System.out.print(pa.get(i) + " ");}System.out.println(pa.get(pa.size() - 1));}}
}
邻接表
import java.util.*;public class Main {static List<List<Integer>> res = new ArrayList<>();static List<Integer> path = new ArrayList<>();public static void dfs(List<LinkedList<Integer>> graph, int now, int n) {// 终止条件:找到一条从1到n的路径if (now == n) {res.add(new ArrayList<>(path));return;}// 遍历当前节点的所有邻接节点for (int i : graph.get(now)) {path.add(i); // 添加当前节点到路径中dfs(graph, i, n); // 递归探索下一节点path.remove(path.size() - 1); // 回溯,移除当前节点}}public static void main(String args[]) {Scanner sc = new Scanner(System.in);int n = sc.nextInt(); // 节点数int m = sc.nextInt(); // 边数// 初始化图的邻接表List<LinkedList<Integer>> graph = new ArrayList<>(n + 1);for (int i = 0; i <= n; i++) {graph.add(new LinkedList<>());}// 构建图的邻接表int a, b;while (m-- > 0) {a = sc.nextInt();b = sc.nextInt();graph.get(a).add(b); // 从a到b的边}// 从节点1开始路径搜索path.add(1); // 初始路径包含节点1dfs(graph, 1, n);// 如果没有路径if (res.isEmpty()) {System.out.println(-1); // 没有路径} else {// 打印所有路径for (List<Integer> re : res) {for (int i = 0; i < re.size() - 1; i++) {System.out.print(re.get(i) + " ");}System.out.println(re.get(re.size() - 1)); // 打印路径的最后一个节点}}}
}岛屿数量
给定一个由 1(陆地)和 0(水)组成的矩阵,你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述:
第一行包含两个整数 N, M,表示矩阵的行数和列数。
后续 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述:
输出一个整数,表示岛屿的数量。如果不存在岛屿,则输出 0。
输入示例:
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例:
3
数据范围:
1 <= N, M <= 50
深搜版
import java.util.Scanner;public class Main {static int cnt = 0; // 用于计数岛屿数量static int direct[][] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}}; // 四个方向的移动// 深度优先搜索public static void dfs(int graph[][], int x, int y, boolean visited[][]) {// 遍历四个方向for (int i = 0; i < 4; i++) {int nextX = x + direct[i][0]; // 下一个位置的x坐标int nextY = y + direct[i][1]; // 下一个位置的y坐标// 判断是否越界if (nextX < 0 || nextY < 0 || nextX >= graph.length || nextY >= graph[0].length) {continue; // 如果越界,跳过}// 如果当前位置是陆地并且未访问过,递归搜索if (!visited[nextX][nextY] && graph[nextX][nextY] == 1) {visited[nextX][nextY] = true; // 标记为已访问dfs(graph, nextX, nextY, visited); // 递归搜索}}}public static void main(String[] args) {int n, m, a;Scanner sc = new Scanner(System.in);n = sc.nextInt(); // 行数m = sc.nextInt(); // 列数int[][] graph = new int[n][m]; // 地图boolean[][] visited = new boolean[n][m]; // 记录每个位置是否已访问// 读取地图for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {a = sc.nextInt();graph[i][j] = a; // 1表示陆地,0表示水域}}// 遍历整个图,每当找到一个未访问的陆地,执行深度优先搜索for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {// 找到一个未访问的陆地,开始深度优先搜索if (!visited[i][j] && graph[i][j] == 1) {cnt++; // 找到一个岛屿visited[i][j] = true; // 标记为已访问dfs(graph, i, j, visited); // 递归搜索整个岛屿}}}// 输出岛屿的数量System.out.println(cnt);}
}另一种写终止条件的写法
public static void dfs(int[][] grid, boolean[][] visited, int x, int y) {// 终止条件:访问过的节点 或者 遇到海水(grid[x][y] == 0)if (visited[x][y] || grid[x][y] == 0) {return;}visited[x][y] = true; // 标记当前位置为已访问// 遍历四个方向for (int i = 0; i < 4; i++) {int nextX = x + dir[i][0];int nextY = y + dir[i][1];// 检查是否越界if (nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) {continue;}// 递归调用 DFSdfs(grid, visited, nextX, nextY);}}
广搜版
- 不少同学用广搜做这道题目的时候,超时了。 这里有一个广搜中很重要的细节:
- 根本原因是只要 加入队列就代表 走过,就需要标记,而不是从队列拿出来的时候再去标记走过。
- 很多同学可能感觉这有区别吗?
- 如果从队列拿出节点,再去标记这个节点走过,就会发生下图所示的结果,会导致很多节点重复加入队列。

import java.util.*;public class Main {// 定义四个方向的偏移量:下、右、上、左public static int[][] dir = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};// 下右上左// 自定义pair类,用于存储坐标static class pair {int first, second;pair(int x, int y) {this.first = x;this.second = y;}}// BFS遍历函数public static void bfs(int[][] grid, boolean[][] visited, int x, int y) {Queue<pair> queue = new LinkedList<pair>(); // 定义坐标队列queue.add(new pair(x, y)); // 入队当前坐标visited[x][y] = true; // 标记当前位置为已访问while (!queue.isEmpty()) {int curX = queue.peek().first; // 获取队列头的X坐标int curY = queue.poll().second; // 获取队列头的Y坐标并出队(poll是把对头元素出队了)// 遍历四个方向for (int i = 0; i < 4; i++) {// 计算下一个坐标int nextX = curX + dir[i][0];int nextY = curY + dir[i][1];// 检查越界if (nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) {continue;}// 如果没有访问过并且该点是陆地(值为1),则入队if (!visited[nextX][nextY] && grid[nextX][nextY] == 1) {queue.add(new pair(nextX, nextY));visited[nextX][nextY] = true; // 标记为已访问}}}}public static void main(String[] args) {Scanner sc = new Scanner(System.in);// 输入网格的行数和列数int m = sc.nextInt();int n = sc.nextInt();int[][] grid = new int[m][n];boolean[][] visited = new boolean[m][n];int ans = 0;// 输入网格的每个值(0为水域,1为陆地)for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {grid[i][j] = sc.nextInt();}}// 遍历网格,查找所有的岛屿for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 如果该点是陆地并且未访问过,则说明发现一个新的岛屿if (!visited[i][j] && grid[i][j] == 1) {ans++; // 岛屿数量加一bfs(grid, visited, i, j); // 通过BFS将该岛屿所有的陆地标记为已访问}}}// 输出岛屿数量System.out.println(ans);}
}岛屿最大面积
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,计算岛屿的最大面积。岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。后续 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示岛屿的最大面积。如果不存在岛屿,则输出 0。
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
4
写在前面
- count是类成员变量,如果不加 static,它们将被视为实例变量,只有通过实例化 Main 类才能访问它们。
- bfs 方法是静态方法,它可以直接通过类名 Main.bfs() 调用。如果不将其设为 static,它就需要依赖于一个 Main 类的实例来调用。
- 如果不加 static,访问count 以及调用 bfs 会出现问题,因为:count 是实例变量,而 bfs 是静态方法。静态方法只能访问静态变量和静态方法。
- 即使你没有实例化 Main 类,你也希望在 main 方法中访问它们,这就要求count 也必须是静态的。
dfs
写法一,dfs只处理下一个节点,即在主函数遇到岛屿就计数为1,dfs处理接下来的相邻陆地
import java.util.*;public class Main {// 定义四个方向的偏移量:右、下、左、上public static int[][] dir = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};static int count; // 记录每次DFS访问的陆地数量// 深度优先搜索 (DFS) 函数public static void dfs(int[][] grid, boolean[][] visited, int x, int y) {for (int i = 0; i < 4; i++) {int nextX = x + dir[i][0];int nextY = y + dir[i][1];// 检查越界if (nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) {continue;}// 如果该位置没有访问过且是陆地,则继续DFSif (!visited[nextX][nextY] && grid[nextX][nextY] == 1) {visited[nextX][nextY] = true;count++; // 增加当前岛屿的陆地数量dfs(grid, visited, nextX, nextY); // 递归访问相邻的陆地}}}public static void main(String[] args) {Scanner sc = new Scanner(System.in);// 输入网格的行数n和列数mint n = sc.nextInt();int m = sc.nextInt();// 创建网格并填充输入数据int[][] grid = new int[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {grid[i][j] = sc.nextInt();}}// 创建一个visited数组,用来标记访问过的位置boolean[][] visited = new boolean[n][m];int result = 0; // 最终记录最大岛屿面积// 遍历每一个格子for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {// 如果当前格子是陆地并且未被访问过,进行DFSif (!visited[i][j] && grid[i][j] == 1) {count = 1; // 这里遇到陆地了,先计数1visited[i][j] = true;dfs(grid, visited, i, j); // 递归访问与当前陆地相连的陆地result = Math.max(result, count); // 更新最大岛屿面积}}}// 输出结果System.out.println(result);}
}
写法二,dfs处理当前节点,即在主函数遇到岛屿就计数为0,dfs处理接下来的全部陆地
// 版本二
import java.util.Scanner;public class Main {// 定义四个方向的偏移量:右、下、左、上public static int[][] dir = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};static int count; // 记录每次DFS访问的陆地数量// 深度优先搜索 (DFS) 函数public static void dfs(int[][] grid, boolean[][] visited, int x, int y) {// 终止条件:访问过的节点 或者 遇到海水if (visited[x][y] || grid[x][y] == 0) return;visited[x][y] = true; // 标记当前位置为已访问count++; // 每访问到一个陆地,计数+1// 遍历四个方向for (int i = 0; i < 4; i++) {int nextX = x + dir[i][0];int nextY = y + dir[i][1];// 检查越界if (nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) {continue;}// 递归调用 DFSdfs(grid, visited, nextX, nextY);}}public static void main(String[] args) {Scanner sc = new Scanner(System.in);// 输入网格的行数n和列数mint n = sc.nextInt();int m = sc.nextInt();// 创建网格并填充输入数据int[][] grid = new int[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {grid[i][j] = sc.nextInt();}}// 创建一个visited数组,用来标记访问过的位置boolean[][] visited = new boolean[n][m];int result = 0; // 最终记录最大岛屿面积// 遍历每一个格子for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {// 如果当前格子是陆地并且未被访问过,进行DFSif (!visited[i][j] && grid[i][j] == 1) {count = 0; // 遇到陆地时先计数为0,进入DFS后开始从1计数dfs(grid, visited, i, j); // 递归访问与当前陆地相连的陆地result = Math.max(result, count); // 更新最大岛屿面积}}}// 输出结果System.out.println(result);}
}大家通过注释可以发现,两种写法,版本一,在主函数遇到陆地就计数为1,接下来的相邻陆地都在dfs中计算。
版本二 在主函数遇到陆地 计数为0,也就是不计数,陆地数量都去dfs里做计算。
bfs的代码省略
孤岛的总面积
目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要计算所有孤岛的总面积,岛屿面积的计算方式为组成岛屿的陆地的总数。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述
输出一个整数,表示所有孤岛的总面积,如果不存在孤岛,则输出 0。
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例:
沉默孤岛
思路
本题要求找到不靠边的陆地面积,那么我们只要从周边找到陆地然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋,然后再去重新遍历地图 统计此时还剩下的陆地就可以了。
Floyd 算法
【题目描述】
小明喜欢去公园散步,公园内布置了许多的景点,相互之间通过小路连接,小明希望在观看景点的同时,能够节省体力,走最短的路径。
给定一个公园景点图,图中有 N 个景点(编号为 1 到 N),以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。
小明有 Q 个观景计划,每个计划都有一个起点 start 和一个终点 end,表示他想从景点 start 前往景点 end。由于小明希望节省体力,他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。
【输入描述】
第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。
接下来的 M 行,每行包含三个整数 u, v, w,表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。
接下里的一行包含一个整数 Q,表示观景计划的数量。
接下来的 Q 行,每行包含两个整数 start, end,表示一个观景计划的起点和终点。
【输出描述】
对于每个观景计划,输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径,则输出 -1。
【输入示例】
7 3 1 2 4 2 5 6 3 6 8 2 1 2 2 3
【输出示例】
4 -1
【提示信息】
从 1 到 2 的路径长度为 4,2 到 3 之间并没有道路。
1 <= N, M, Q <= 1000.
思路
Floyd算法核心思想是动态规划。
-
例如我们再求节点1 到 节点9 的最短距离,用二维数组来表示即:grid[1][9],如果最短距离是10 ,那就是 grid[1][9] =10。
-
那 节点1 到 节点9 的最短距离 是不是可以由 节点1 到节点5的最短距离 + 节点5到节点9的最短距离组成呢? 即 grid[1][9] = grid[1][5] + grid[5][9]
-
节点1 到节点5的最短距离 是不是可以有 节点1 到 节点3的最短距离 + 节点3 到 节点5 的最短距离组成呢? 即 grid[1][5] = grid[1][3] + grid[3][5]
-
以此类推,节点1 到 节点3的最短距离 可以由更小的区间组成。那么这样我们是不是就找到了,子问题推导求出整体最优方案的递归关系呢。
-
节点1 到 节点9 的最短距离 可以由 节点1 到节点5的最短距离 + 节点5到节点9的最短距离组成, 也可以有 节点1 到节点7的最短距离 + 节点7 到节点9的最短距离的距离组成。
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt(); // 顶点数int m = sc.nextInt(); // 边数// 初始化距离矩阵,最大值设置为10005final int INF = 10005;int[][] grid = new int[n + 1][n + 1];// 初始化 grid 数组for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (i != j) {grid[i][j] = INF;}}}// 输入边信息for (int i = 0; i < m; i++) {int p1 = sc.nextInt();int p2 = sc.nextInt();int val = sc.nextInt();grid[p1][p2] = val;grid[p2][p1] = val; // 双向图}// Floyd-Warshall 算法//注意k要放在最外层for (int k = 1; k <= n; k++) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (grid[i][k] + grid[k][j] < grid[i][j]) {grid[i][j] = grid[i][k] + grid[k][j];}}}}// 输出查询结果int z = sc.nextInt(); // 查询次数while (z-- > 0) {int start = sc.nextInt();int end = sc.nextInt();if (grid[start][end] == INF) {System.out.println(-1);} else {System.out.println(grid[start][end]);}}sc.close(); // 关闭Scanner}
}dijkstra(朴素版)
【题目描述】
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。
小明的起点是第一个车站,终点是最后一个车站。然而,途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素(如天气变化)等不同,这些因素都会影响每条路径的通行时间。
小明希望能选择一条花费时间最少的路线,以确保他能够尽快到达目的地。
【输入描述】
第一行包含两个正整数,第一个正整数 N 表示一共有 N 个公共汽车站,第二个正整数 M 表示有 M 条公路。
接下来为 M 行,每行包括三个整数,S、E 和 V,代表了从 S 车站可以单向直达 E 车站,并且需要花费 V 单位的时间。
【输出描述】
输出一个整数,代表小明从起点到终点所花费的最小时间。
思路
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组
- minDist数组 用来记录 每一个节点距离源点的最小距离。
- 示例中节点编号是从1开始,所以为了让大家看的不晕,minDist数组下标我也从 1 开始计数,下标0 就不使用了,这样 下标和节点标号就可以对应上了,避免大家搞混
模拟过程
0、初始化
minDist数组数值初始化为int最大值。
这里在强点一下 minDist数组的含义:记录所有节点到源点的最短路径,那么初始化的时候就应该初始为最大值,这样才能在后续出现最短路径的时候及时更新。

源点(节点1) 到自己的距离为0,所以 minDist[1] = 0
此时所有节点都没有被访问过,所以 visited数组都为0
- 模拟过程
以下为dijkstra 三部曲
1.1 第一次模拟
1、选源点到哪个节点近且该节点未被访问过
源点距离源点最近,距离为0,且未被访问。
2、该最近节点被标记访问过
标记源点访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:

更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
源点到节点2的最短距离为1,小于原minDist[2]的数值max,更新minDist[2] = 1
源点到节点3的最短距离为4,小于原minDist[3]的数值max,更新minDist[3] = 4
1.2 第二次模拟
1、选源点到哪个节点近且该节点未被访问过
未访问过的节点中,源点到节点2距离最近,选节点2
2、该最近节点被标记访问过
节点2被标记访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:

更新 minDist数组,即:源点(节点1) 到 节点6 、 节点3 和 节点4的距离。
以后的过程以此类推
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);// 输入节点数 n 和边数 mint n = sc.nextInt();int m = sc.nextInt();// 定义一个邻接矩阵,初始化为一个很大的数final int INF = Integer.MAX_VALUE;int[][] grid = new int[n + 1][n + 1];// 初始化 grid 为 INF,表示没有直接路径for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (i != j) {grid[i][j] = INF;}}}// 输入边的信息for (int i = 0; i < m; i++) {int p1 = sc.nextInt();int p2 = sc.nextInt();int val = sc.nextInt();grid[p1][p2] = val;}// 设置起点和终点int start = 1;int end = n;// 存储从源点到每个节点的最短距离int[] minDist = new int[n + 1];// 记录顶点是否被访问过boolean[] visited = new boolean[n + 1];// 初始化最短距离数组,起始点到自身的距离为0,其他为INFfor (int i = 1; i <= n; i++) {minDist[i] = INF;}minDist[start] = 0;// 遍历所有节点,执行Dijkstra算法for (int i = 1; i <= n; i++) {int minVal = INF;int cur = -1;// 选择距离起点最近且未访问过的节点for (int v = 1; v <= n; v++) {if (!visited[v] && minDist[v] < minVal) {minVal = minDist[v];cur = v;}}// 如果当前节点无法访问,则跳出循环(即剩下的节点不可达)if (cur == -1) break;visited[cur] = true; // 标记该节点已被访问// 更新非访问节点到源点的最短距离for (int v = 1; v <= n; v++) {if (!visited[v] && grid[cur][v] != INF && minDist[cur] + grid[cur][v] < minDist[v]) {minDist[v] = minDist[cur] + grid[cur][v];}}}// 输出结果,如果终点不可达,输出 -1if (minDist[end] == INF) {System.out.println(-1);} else {System.out.println(minDist[end]);}sc.close(); // 关闭Scanner}
}
最小生成树之prim
卡码网:53.寻宝
题目描述:
在世界的某个区域,有一些分散的神秘岛屿,每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路,方便运输。
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将 所有岛屿联通起来。
给定一张地图,其中包括了所有的岛屿,以及它们之间的距离。以最小化公路建设长度,确保可以链接到所有岛屿。
输入描述:
第一行包含两个整数V 和 E,V代表顶点数,E代表边数 。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
接下来共有 E 行,每行三个整数 v1,v2 和 val,v1 和 v2 为边的起点和终点,val代表边的权值。
输出描述:
输出联通所有岛屿的最小路径总距离
输入示例:
7 11
1 2 1
1 3 1
1 5 2
2 6 1
2 4 2
2 3 2
3 4 1
4 5 1
5 6 2
5 7 1
6 7 1
输出示例:
6
思路
-
第一步,选距离生成树最近节点
-
第二步,最近节点加入生成树
-
第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
-
minDist数组用来记录 每一个节点距离最小生成树的最近距离。
-
示例中节点编号是从1开始,minDist数组下标也从 1 开始计数。
初始状态
minDist 数组 里的数值初始化为 最大数,因为本题 节点距离不会超过 10000,所以 初始化最大数为 10001就可以。
现在 还没有最小生成树,默认每个节点距离最小生成树是最大的,这样后面我们在比较的时候,发现更近的距离,才能更新到 minDist 数组上。

模拟过程(只模拟两轮)
第一轮
1、prim三部曲,第一步:选距离生成树最近节点
选择距离最小生成树最近的节点,加入到最小生成树,刚开始还没有最小生成树,所以随便选一个节点加入就好(因为每一个节点一定会在最小生成树里,所以随便选一个就好),那我们选择节点1 (符合遍历数组的习惯,第一个遍历的也是节点1)
2、prim三部曲,第二步:最近节点加入生成树
此时 节点1 已经算最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)

注意图中我标记了 minDist数组里更新的权值,是哪两个节点之间的权值,例如 minDist[2] =1 ,这个 1 是 节点1 与 节点2 之间的连线,清楚这一点对最后我们记录 最小生成树的权值总和很重要。
第二轮
1、prim三部曲,第一步:选距离生成树最近节点
选取一个距离 最小生成树(节点1) 最近的非生成树里的节点,节点2,3,5 距离 最小生成树(节点1) 最近,选节点 2(其实选 节点3或者节点2都可以,距离一样的)加入最小生成树。
2、prim三部曲,第二步:最近节点加入生成树
此时 节点1 和 节点2,已经是最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来,我们要更新节点距离最小生成树的距离,如图:

import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int v = scanner.nextInt();int e = scanner.nextInt();// 初始化邻接矩阵,所有值初始化为一个大值,表示无穷大int[][] grid = new int[v + 1][v + 1];for (int i = 1; i <= v; i++) {Arrays.fill(grid[i], 10001);}// 读取边的信息并填充邻接矩阵for (int i = 0; i < e; i++) {int x = scanner.nextInt();int y = scanner.nextInt();int k = scanner.nextInt();grid[x][y] = k;grid[y][x] = k;}// 所有节点到最小生成树的最小距离int[] minDist = new int[v + 1];Arrays.fill(minDist, 10001);// 记录节点是否在树里boolean[] isInTree = new boolean[v + 1];// Prim算法主循环 只需要循环v-1次建立v-1条边for (int i = 1; i < v; i++) {int cur = -1;// 用于记录距离生成树最近的节点int minVal = Integer.MAX_VALUE; // 记录最短距离// 选择距离生成树最近的节点for (int j = 1; j <= v; j++) {// 如果这个点不在生成树里面,且它的距离小于当前最小值if (!isInTree[j] && minDist[j] < minVal) {minVal = minDist[j];cur = j;}}// 将最近的节点加入生成树isInTree[cur] = true;// 更新非生成树节点到生成树的距离for (int j = 1; j <= v; j++) {//当前cur节点比较if (!isInTree[j] && grid[cur][j] < minDist[j]) {minDist[j] = grid[cur][j];}}}// 统计结果int result = 0;for (int i = 2; i <= v; i++) {result += minDist[i];// 从2开始,跳过起始节点}System.out.println(result);scanner.close();}
}kruskal算法
- 题目同上题,找最小生成树。
思路
- prim 算法是维护节点的集合,而 Kruskal 是维护边的集合。
- 边的权值排序,因为要优先选最小的边加入到生成树里
- 遍历排序后的边
- 如果边首尾的两个节点在同一个集合,说明如果连上这条边图中会出现环
- 如果边首尾的两个节点不在同一个集合,加入到最小生成树,并把两个节点加入同一个集合
模拟

排序后的边顺序为[(1,2) (4,5) (1,3) (2,6) (3,4) (6,7) (5,7) (1,5) (3,2) (2,4) (5,6)]
(1,2) 表示节点1 与 节点2 之间的边。权值相同的边,先后顺序无所谓。
开始从头遍历排序后的边。
选边(1,2),节点1 和 节点2 不在同一个集合,所以生成树可以添加边(1,2),并将 节点1,节点2 放在同一个集合。
 选边(4,5),节点4 和 节点 5 不在同一个集合,生成树可以添加边(4,5) ,并将节点4,节点5 放到同一个集合。
选边(4,5),节点4 和 节点 5 不在同一个集合,生成树可以添加边(4,5) ,并将节点4,节点5 放到同一个集合。

在上面的讲解中,看图的话 大家知道如何判断 两个节点 是否在同一个集合(是否有绿色的线连在一起),以及如何把两个节点加入集合(就在图中把两个节点连上)
- 但在代码中,如果将两个节点加入同一个集合,又如何判断两个节点是否在同一个集合呢?
- 用并查集
import java.util.*;class Edge {int l, r, val;Edge(int l, int r, int val) {this.l = l;this.r = r;this.val = val;}
}
public class Main {private static int n = 10001;private static int[] father = new int[n];// 并查集初始化public static void init() {for (int i = 0; i < n; i++) {father[i] = i;}}// 并查集的查找操作public static int find(int u) {if (u == father[u]) return u;return father[u] = find(father[u]);}public static void join(int u, int v) {u = find(u);v = find(v);if (u == v) return;father[v] = u;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int v = scanner.nextInt();int e = scanner.nextInt();List<Edge> edges = new ArrayList<>();int result_val = 0;for (int i = 0; i < e; i++) {int v1 = scanner.nextInt();int v2 = scanner.nextInt();int val = scanner.nextInt();edges.add(new Edge(v1, v2, val));}//对边进行排序edges.sort(Comparator.comparingInt(edge -> edge.val));// 并查集初始化init();// 从头开始遍历边for (Edge edge : edges) {int x = find(edge.l);int y = find(edge.r);if (x != y) {result_val += edge.val;join(x, y);}}System.out.println(result_val);scanner.close();}
}相关文章:

图论-代码随想录刷题记录[JAVA]
文章目录 前言深度优先搜索理论基础所有可达路径岛屿数量岛屿最大面积孤岛的总面积沉默孤岛Floyd 算法dijkstra(朴素版)最小生成树之primkruskal算法 前言 新手小白记录第一次刷代码随想录 1.自用 抽取精简的解题思路 方便复盘 2.代码尽量多加注释 3.记录…...

c#加载shellcode
本地加载bin文件 SharpPELoader项目如下: using System; using System.IO; using System.Runtime.InteropServices;namespace TestShellCode {internal class Program{private const uint MEM_COMMIT 0x1000;private const uint PAGE_EXECUTE_READWRITE 0x40;pr…...

HarmonyOS 开发环境搭建
HarmonyOS(鸿蒙操作系统)作为一种面向全场景多设备的智能操作系统,正逐渐在市场上崭露头角。为了进入HarmonyOS生态,开发者需要搭建一个高效的开发环境。本文将详细介绍如何搭建HarmonyOS开发环境,特别是如何安装和配置…...

【网络云计算】2024第46周周考-磁盘管理的基础知识-RAID篇
文章目录 1、画出各个RAID的结构图,6句话说明优点和缺点,以及磁盘可用率和坏盘数量,磁盘总的数量2、写出TCP五层模型以及对应的常用协议 【网络云计算】2024第46周周考-磁盘管理的基础知识-RAID篇 1、画出各个RAID的结构图,6句话说…...

深入理解 SQL_MODE 之 ANSI_QUOTES
引言 在 MySQL 数据库中,sql_mode 是一个重要的配置参数,它定义了 MySQL 应该遵循的 SQL 语法标准以及数据验证规则。其中,ANSI_QUOTES 是 sql_mode 中的一个重要选项,它改变了 MySQL 对于字符串和标识符的识别方式,使…...

容器技术在持续集成与持续交付中的应用
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 容器技术在持续集成与持续交付中的应用 容器技术在持续集成与持续交付中的应用 容器技术在持续集成与持续交付中的应用 引言 容器…...

【嵌入式软件-STM32】OLED显示屏+调试方法
目录 一、调试方式 1)串口调试 优势 弊端 2)显示屏调试 优势 弊端 3)Keil调试模式 4)点灯调试法 5)注释调试法 6)对照法 二、OLED简介 OLED组件 OLED显示屏 0.96寸OLED模块 OLED外观和种类…...
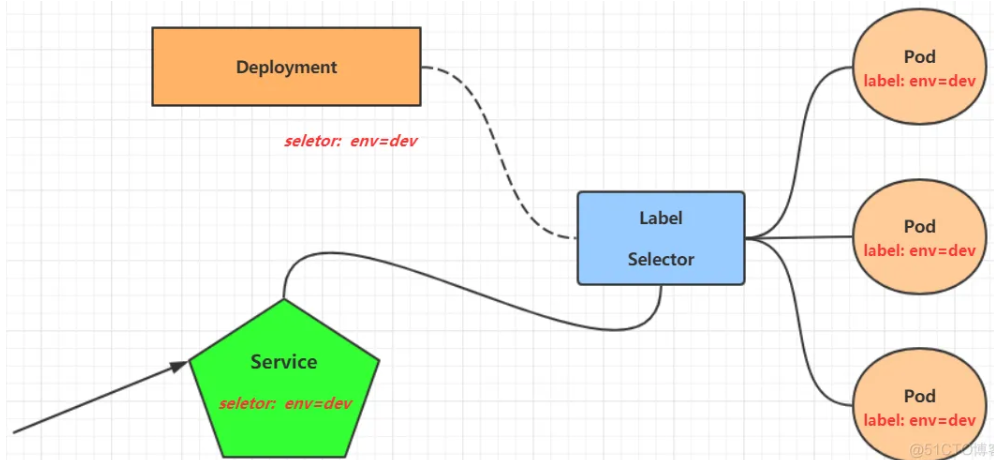
kubernetes简单入门实战
本章将介绍如何在kubernetes集群中部署一个nginx服务,并且能够对其访问 Namespace Namespace是k8s系统中一个非常重要的资源,它的主要作用是用来实现多套环境的资源隔离或者多租户的资源隔离。 默认情况下,k8s集群中的所有的Pod都是可以相…...

Python连接Mysql、Postgre、ClickHouse、Redis常用库及封装方法
博主在这里分享一些常见的python连接数据库或中间件的库和封装方案,希望对大家有用。 Mysql封装 #!/usr/bin/python # -*- coding: utf-8 -*- import sys import pymysql from settings import MYSQL_DB, MYSQL_PORT, MYSQL_USER, MYSQL_PASSWORD, MYSQL_HOST, EN…...

如何修改npm包
前言 开发中遇到一个问题,配置 Element Plus 自定义主题时,添加了 ElementPlusResolver({ importStyle: "sass" }) 后,控制台出现报错,这是因为 Dart Sass 2.0 不再支持使用 !global 来声明新变量,虽然当前…...

Django 2024全栈开发指南(三):数据库模型与ORM操作(上篇)
目录 一、模型的定义二、数据迁移三、数据表关系四、数据表操作4.1 Shell工具4.2 数据新增4.3 数据修改4.4 数据删除4.5 数据查询 Django 对各种数据库提供了很好的支持,包括 PostgreSQL、MySQL、SQLite 和 Oracle,而且为这些数据库提供了统一的 API 方法…...

低代码可视化-uniapp开关选择组件-低码生成器
开关(Switch)选择组件是一种用户界面元素,允许用户在两种状态(通常是开/关、是/否、启用/禁用等)之间进行切换。这种组件在移动应用、桌面软件、网页以及物联网设备中广泛应用。以下是对开关Switch选择组件的详细介绍&…...

【arxiv‘24】Vision-Language Navigation with Continual Learning
论文信息 题目:Vision-Language Navigation with Continual Learning 视觉-语言导航与持续学习 作者:Zhiyuan Li, Yanfeng Lv, Ziqin Tu, Di Shang, Hong Qiao 论文创新点 VLNCL范式:这是一个新颖的框架,它使得智能体能够在适…...
如何在 Ubuntu 上安装 Jupyter Notebook
本篇文章将教你在 Ubuntu 服务器上安装 Jupyter Notebook,并使用 Nginx 和 SSL 证书进行安全配置。 我将带你一步步在云服务器上搭建 Jupyter Notebook 服务器。Jupyter Notebook 在数据科学和机器学习领域被广泛用于交互式编码、可视化和实验。在远程服务器上运行…...
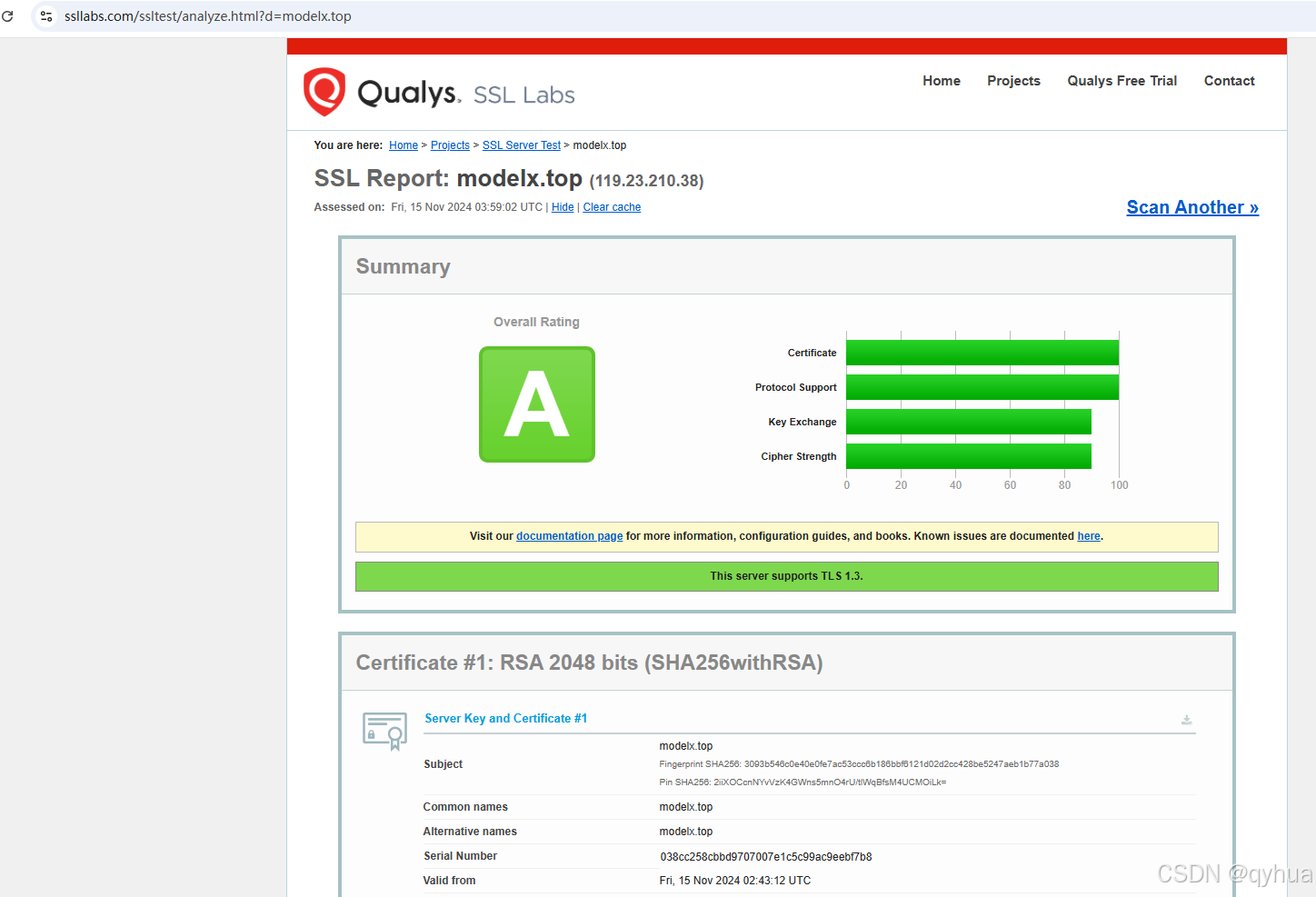
免费申请 Let‘s Encrypt SSL 证书
免费申请 Lets Encrypt SSL 证书 在网络安全日益重要的今天,为网站启用 SSL 证书是保障数据安全和用户信任的关键。Lets Encrypt 提供的免费 SSL 证书是一个很好的选择。下面我们详细介绍如何为网站域名申请该证书。 一、准备工作 域名 确保已注册要使用 SSL 证书的…...

【JAVA】Java基础—面向对象编程:继承—重写父类方法
在Java开发中,重写(Override)是面向对象编程(OOP)中的一个重要概念。它允许子类提供父类方法的具体实现,从而改变或扩展父类的行为。重写是实现多态性的重要手段,使得程序在运行时能够根据对象的…...

【C++初阶】C++入门
1、C第一个程序 C是脱胎于C语言的,所以也包含了C语言绝大多数的内容,C兼容C语言绝大多数的语法,在C语言中能实现的程序在C中也是可以执行的,但需要将定义文件代码的后缀改为.cpp 就比如hello world程序 // test.cpp #include<stdio.h&g…...

自然推理系统:的拒取式的解析
要推导出 **"非A"** 的拒取式 (rejection form),首先我们要理解逻辑推理中几个基本的概念。 假设我们有以下前提: 1. **A → B** (如果A成立,那么B成立) 2. **非B** (B不成立) 我们…...
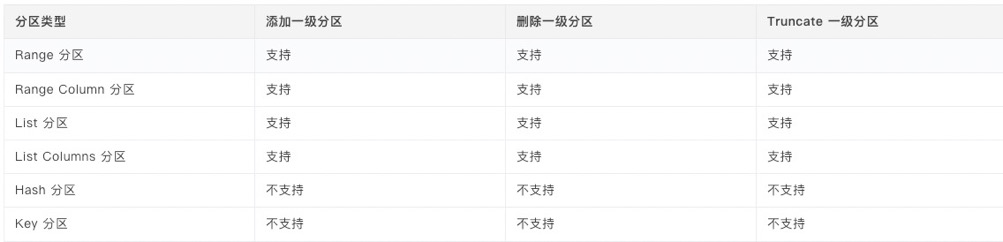
OceanBase 分区表详解
1、分区表的定义 在OceanBase数据库中,普通的表数据可以根据预设的规则被分割并存储到不同的数据区块中,同一区块的数据是在一个物理存储上。这样被分区块的表被称为分区表,而其中的每一个独立的数据区块则被称为一个分区。 如下图所示&…...

Java中 LinkedList<>,ArrayDeque<>的区别 || Queue和Deque的区别
我是你爹 LinkedList<> 和 ArrayDeque<> 的区别Queue接口 和 Deque接口区别Queue 的用法Deque 的用法 LinkedList<> 和 ArrayDeque<> 的区别 1. 数据结构实现方式: LinkedList: 基于链表结构,是一个双向链表。每个…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
