论文阅读 - Causally Regularized Learning with Agnostic Data Selection

代码链接: GitHub - HMTTT/CRLR: CRLR尝试实现
https://arxiv.org/pdf/1708.06656v2
目录
摘要
INTRODUCTION
2 RELATED WORK
3 CAUSALLY REGULARIZED LOGISTIC REGRESSION
3.1 Problem Formulation
3.2 Confounder Balancing
3.3 Causally Regularized Logistic Regression
3.4 Optimization
3.5 Complexity Analysis
4 EXPERIMENTS0
4.2 Baselines
4.3 Experiments on Synthetic Data
4.4 Experiments on YFCC100M Dataset
摘要
之前的大部分机器学习算法都是基于 i.i.d 提出的。假设。然而,这种理想的假设在实际应用中经常被违反,其中训练和测试过程之间可能会出现选择偏差。此外,在许多场景中,测试数据在训练过程中甚至不可用,这使得迁移学习等传统方法由于需要测试分布的先验而变得不可行。因此,如何解决鲁棒模型学习的不可知选择偏差对于学术研究和实际应用都至关重要。
本文在假设变量间的因果关系在不同领域间具有稳健性的前提下,将因果技术融入预测建模中,通过联合优化全局混杂因素平衡和加权逻辑回归,提出了一种新颖的因果正则化逻辑回归(CRLR)算法。
全局混杂因素平衡有助于识别因果特征,这些特征对结果的因果影响在不同领域是稳定的,然后对这些因果特征进行逻辑回归,从而构建一个稳健的预测模型,避免不可知论偏差。
为了验证 CRLR 算法的有效性,在合成数据集和真实数据集上进行了全面实验。实验结果清楚地表明,CRLR 算法优于最先进的方法,并且方法的可解释性可以通过特征可视化来充分描述。
INTRODUCTION
传统机器学习中的一个常见假设是,测试数据与训练数据独立地来自同一分布(即 i.i.d 假设)。这样,从训练数据中学到的模型就可以直接用于对测试数据进行经验误差最小的预测。违反 i.i.d. 假设所带来的危险和风险在传统的机器学习方法中往往被忽视,尽管这些方法在许多棘手的任务中取得了显著的成功,如图像分类、语音识别、物体定位等。然而,在许多实际应用中,无法完全控制数据收集过程,因此选择偏差可能会导致违反 i.i.d. 假设。
此外,在大多数情况下,测试数据在训练过程中是不可见的,因此测试数据的选择偏差变得不可知。因此,如果不考虑不可知的数据选择偏差,现有的预测模型在不同偏差的数据上就会缺乏鲁棒性,其预测结果也可能不可靠。
如图 1 所示,识别狗的分类器主要通过狗在草地上的图像进行训练,而通过狗在草地上的图像进行测试(即 i.i.d.情况下)和另一张雪地里有一只狗的图像(即非 i.i.d.情况下)。基于相关性的方法在 i.i.d. 案例中取得了成功,但在非 i.i.d. 案例中却失败了。失败的主要原因是,由于草地特征与训练集中的标签高度相关,因此在分类器中被赋予了较高的权重,但它们并没有出现在测试图像中。

相关工作:解决选择偏差的问题
最近,有几篇文献旨在解决由选择偏差引起的非同义问题。
基于特征空间转换[8, 19, 21, 27]、不变特征学习[10, 33]和分布匹配[20, 34],提出了多种领域适应方法。
然而,这些方法都需要测试数据的先验知识,而在某些实际应用中可能无法获得这些先验知识。
为克服这一难题,人们提出了领域泛化方法,主要基于仅使用训练数据学习领域无关模型或不变表示的理念[11, 17, 22]。
这些方法假定训练数据中存在已知的选择偏差(由不同领域描述),因此不能很好地泛化到不可知的选择偏差。
在这项工作中,在不知道测试数据或训练数据的领域信息的情况下,研究了在不可知数据选择偏差的数据上进行学习的问题。与之前的所有工作相比,目标定位问题更具普遍性,在实际应用中也更实用。
解决不可知论选择偏差方法介绍:因果推断
解决不可知论选择偏差的一个合理方法是学习带有因果变量的预测模型,这些因果变量对结果变量的影响对选择偏差不敏感。
因果推理是发现因果变量和结构的强大统计工具。
由于在确定因果变量时对混杂影响进行了严格审查[26],因果变量在不同领域或数据选择偏差中具有稳定性,这一点已得到公认。
因果变量的稳定性主要体现在给定这些因果变量的结果变量的条件分布在不同领域保持不变。
相反,相关变量则不具备这一特性。
确定变量因果影响的黄金标准是进行 A/B 测试等随机化实验。但完全随机化实验通常成本高昂,在某些情况下甚至不可行。
尽管如此,只要满足无混杂性假设[26],即所有混杂因素都包括在内,并且在给定观察变量时,treatment(干预)分布与潜在结果无关,就可以直接从观察数据中精确估计因果效应。
近来,基于观察数据的因果推断开始流行起来,具有代表性的方法包括倾向得分匹配或再加权[2, 3, 15]、马尔可夫毯[13, 25]和混杂因素平衡[1, 12, 14]等。然而,这些方法大多旨在估计变量对输出的因果影响,很少有方法利用因果关系的优势,特别是在预测建模中不同环境下的稳定性。
因果分析与非独立同分布相结合的挑战
追求将因果分析与非独立同分布相结合。学习上,还面临两个挑战。首先,现有的因果分析方法是在精心设计的环境中提出的,通常只考虑少量的干预变量;因为在机器学习问题的高维设置中,对因果关系的先验知识很少,因此必须将所有变量都视为干预变量。这使得现有的因果模型因计算复杂而不可行。
此外,虽然可以首先选择因果变量,然后根据这些变量学习模型,但这种方法在统计上对因果变量选择的阈值很敏感,而且这种分步方法在实践中很难优化。因此,要为有数据选择偏差的预测问题设计一种可扩展的因果学习方法是非常困难的。
在本文中,主要考虑分类问题,并提出了一种新颖的因果正则化逻辑回归(CRLR)模型,用于对不可知选择偏差的数据进行分类。
该模型由一个加权逻辑损失项和一个微妙的去符号因果正则化器组成。
具体来说,因果正则调节器通过样本再加权直接平衡每个干预特征的混杂因素分布。
为了降低模型的复杂性,提出了一种全局样本再加权方法,通过学习共同的样本再加权矩阵来最大限度地平衡所有干预特征的混杂因素。
通过这种方法,加权逻辑损失和因果正则被联合优化,从而得到既有预测能力又有因果含义的回归系数。
这些优点使得生成的模型能够准确、稳定地进行预测,而不会受到不可知论选择偏差的严重影响。
本文在技术上有三方面的贡献:
研究了一个新的问题,即如何在具有不可知选择偏差的数据上进行学习。这个问题的设置比之前的领域适应和领域基因化等工作更普遍,在实际应用中也更实用。
将因果推理引入预测建模,并提出了一种新的因果正则化逻辑回归模型来解决上述问题,在该模型中,因果正则化和预测损失以一种有效的方式得到了联合优化。
在合成数据和真实数据中进行了广泛的实验,实验结果表明,方法在学习具有不可知偏差的数据时非常有效。方法的可解释性也是一个显著的优点。
2 RELATED WORK
在本节中,将简要回顾和讨论之前的相关工作,这些工作可分为领域适应、领域泛化和因果推理。
领域适应
为了解决非 i.i.d. 问题,人们提出了多种域适应方法。域适应的一种直观方法是移动源域分布以对齐目标主域分布,并提出了多种技术,如重新检测采样 [34] 和偏差感知概率方法 [18]。另一种直觉是学习特征空间的变换或直接学习领域不变的特征表示[8, 10, 19- 21, 27, 33],利用强大的表示学习技术,如深度神经网络。
领域泛化
与领域适应密切相关的任务是领域泛化,而测试数据是在训练过程中无法使用。在这种情况下,领域无关分类器 [11, 17, 22] 是在多领域训练数据上学习的,并应用于对未见领域的预测。上述所有方法都需要测试数据的先验知识或训练数据的明确域分离,这在许多实际应用中都是不切实际的。
不可知选择偏差
在这项工作中,研究了一个更具普遍性和挑战性的问题,即在训练数据和测试数据的偏差都未知的情况下,如何在不可知选择偏差的数据上进行学习。目标问题有别于之前的研究,在实际场景中更加实用。
因果推断是一种强大的统计建模工具,可用于前计划性分析。估计因果效应的主要问题是平衡不同干预水平的混杂因素分布。罗森鲍姆和鲁宾[26]建议通过倾向得分匹配或再加权来实现平衡。基于倾向分数的方法已广泛应用于各个领域,包括经济学[28]、流行病学[9]、医疗保健[7]、社会科学[16]和广告学[29]。但这些方法只能处理一个或少数几个处理变量,无法直接应用于多媒体任务,因为在多媒体任务中,通常有大量特征被视为潜在的处理变量。有越来越多的文献提出直接优化样本权重以平衡混杂因素分布。Hainmueller [12] 提出了通过指定样本矩直接调整样本权重的方法。Athey 等人[1] 提出了通过拉索残差回归调整样本权重学习的近似残差平衡。Kuang等人[14]学习了不同的混杂因素权重和平衡混杂因素分布来估计干预效果。这些方法提供了一种在没有先验知识结构的情况下估算因果影响的有效方法,但它们对以单一干预变量为目标的样本进行了再加权,不能直接应用于预测建模。作者将调整重权平衡技术,使其适用所针对的大规模因果影响评估设置。
3 CAUSALLY REGULARIZED LOGISTIC REGRESSION
介绍问题的提出、因果推断的一些关键概念的初步介绍、混杂因素平衡以及提出的因果正规化逻辑回归(CRLR)方法的详细介绍。
3.1 Problem Formulation
将目标问题--具有不可知论选择偏差的数据分类--表述如下:
Problem 1 (Classification on Data with Agnostic Selection Bias).
给定训练数据:,
代表特征,
代表标签,任务是学习一个分类器
用参数θ精确预测测试数据的标签
,
, 在不可知的选择偏差设置中,不知道分布如何从训练数据转移到看不见的测试数据。
为了解决这个具有挑战性的问题,引入了因果关系这一强大的统计建模工具. 因果推理是估计每个变量对结果的因果影响,或者换句话说,确定因果变量,而因果变量可以直接由珀尔因果 DAG [24] 中结果的父节点确定。当将每个变量设定为干预变量以估计其对结果的因果影响时,其他变量被视为混杂变量。如前所述,因果变量在不同选择偏差下的稳定性使其比相关变量更适合目标问题。为了将因果推理应用到分类问题中,将每个特征 视为处理变量(即治疗),将所有剩余特征 X-j = X\ Xj 视为混杂变量(即合并变量),将标签 Y 视为结果变量。
由于对因果结构没有先验知识,因此将每个变量视为治疗变量,而将所有其他变量视为混合变量 是一种合理的方法[12]。在不失一般性的前提下,为了便于讨论和理解,假设所有特征和标签都是二进制的(分类和连续特征可以通过二进制和单次编码转换为二进制特征)。给定一个特征作为处理,如果该特征在样本中出现(或不出现),则该样本成为处理(或对照)样本。为了安全地估计给定特征 Xj 对标签 Y 的因果贡献,必须消除混杂偏差,混杂偏差是由混杂因素 X-j 在处理组和对照组之间的不同分布引起的。在消除混杂偏差后处理组和对照组之间标签 Y 的差异可以被视为特征 Xj 对标签 Y 的因果贡献。
由于因果贡献率 β∈在不同领域都是稳健而稳定的,因此可以将具有不可知论选择偏差的数据分类问题无缝转换为以下因果分类问题。
Problem 2 (Causal Classification Problem).
给定训练数据 D = (X, Y),其中 X ∈ 表示特征,Y∈
表示标签,任务是联合识别所有特征的因果贡献 β∈
,并根据 β 学习分类器 fβ (-),进行分类。
因果分类问题的关键挑战在于如何联合优化因果贡献识别和分类。在本文中,作者提出了一种由因果正则和逻辑回归项组成的协同学习算法。
3.2 Confounder Balancing
在此,简要介绍混杂因素平衡的一些必要背景,这将对设计因果正则器有所启发。在观察性研究中,需要平衡混杂因素的分布,以纠正非随机分配带来的偏差。由于矩可以唯一地确定一个分布,混杂因素平衡方法通过调整样本权重来直接平衡混杂因素矩[1, 12, 14]。样本权重 W 的学习方法如下:

给定一个干预特征 T,和
分别代表有干预和无干预样本中混杂因素的平均值。平衡混杂因素后,处理变量与输出变量之间的相关性代表了因果影响。在公式 1 中只考虑了一阶矩(适用于二元变量),通过加入更多特征,可以很容易地纳入高阶矩。请注意,混杂因素平衡技术旨在估计单个干预特征的因果效应。在例子中,需要估计所有特征的因果影响。这意味着需要学习 p × n 样本权重,这在高维场景中显然是不可行的。因此,在 3.3 节中提出了一种全局平衡方法作为因果正则化器。
3.3 Causally Regularized Logistic Regression
受混杂因素平衡法的启发,提出了一种因果正则器,将每个特征连续设置为干预变量,并找到一组最佳样本权重,使每个处理变量的处理组和对照组分布均衡。

其中 W 是样本权重。整体表示将特征 j 设为干预变量时混杂因素平衡的损失,X-j 表示所有剩余特征(即混杂因素),将其第 j 列替换为 0 后即为 X。Ij 指 I 的第 j 列,指将特征 j 设为处理变量时单位 i 的处理状态。然后,将因果正则和逻辑回归模型结合起来,提出了因果正则化逻辑回归(CRLR)算法,以共同优化样本权重 W 和回归因子 β:

其中,![]() 表示加权逻辑损失。
表示加权逻辑损失。
弹性网约束![]() 有助于避免过度拟合。
有助于避免过度拟合。
W 0 约束每个样本权重为非负值。
在规范![]() 的情况下,可以减小样本权重的方差,从而达到稳定的目的。
的情况下,可以减小样本权重的方差,从而达到稳定的目的。
公式 ![]() 可以避免所有样本权重为 0。
可以避免所有样本权重为 0。
在传统的逻辑回归模型中,回归系数反映了特征与标签之间的相关性。但由于混杂偏差,高度相关的特征并不意味着因果关系。在模型中,从因果正则器中学习到的样本权重能够纠正偏差,并在全局平衡任何处理特征的处理组和对照组的分布。因此,估计的系数 β 可以同时暗示因果关系和对标签的预测能力。
3.4 Optimization
对公式 3 中的上述模型进行优化的目标是:在参数 W 和 β 的约束下最小化 J (W , β)。

对于公式 4 中的最终优化问题,很难得到一个分析解。采用迭代优化算法来解决这个问题。
首先,初始化样本权重 W 和因果贡献率 β,然后在每次迭代中,先通过修正 W 更新 β,再通过修正 β 更新 W:
更新 β: 固定 W 时,问题 (4) 等价于优化以下目标函数:

这是一个标准的 ℓ1 和 ℓ2 规范正则化最小二乘问题,可以用任何弹性网求解器求解。在这里,使用近似梯度算法[23]和近似算子来优化 (5) 中的目标函数。
更新 W:固定,通过优化 (4)可以得到 W。这等同于优化以下目标函数:

为确保 W 的非负性,设 W = ω ⊙ ω,其中 ω∈ ,⊙ 指 Hadamard 积(逐元素相乘积)。那么问题(6)可以重拟为:

项 J (ω) 相对于 ω 的部分梯度为:

![]()

然后, 通过线搜索确定步长 a,使用梯度下降更新 ω,并在第 t 次迭代时更新 :

之后,计算损失值J(W)
反复更新 β 和 W,直到目标函数 (4) 收敛。
3.5 Complexity Analysis
在优化过程中,主要代价是计算损失 J (W , β)、更新因果特征权重 β 和样本权重 W。将逐一分析其时间复杂性。
对于损失的计算,其复杂度为 O(),其中 n 是样本大小,p 是变量维度。对于更新 β,这是一个标准的弹性网问题,其复杂度为 O(np)。
对于更新 W,复杂度主要取决于计算函数 J (ω) 相对于变量 ω 的部分梯度的步骤。∂ J(ω) / ∂ω 的复杂度为 O()。
4 EXPERIMENTS0
合成数据集: 生成具有独立高斯分布的预测变量 X = {C, V} ∼ N (0, 1),其中预测变量 X 分为两部分:因果变量 C 和噪声变量 V。为了使 Y 成为二进制变量,如果 Y ≥ 0,我们设置 Y = 1,否则 Y = 0。为了测试算法在不可知选择偏差数据上的有效性,通过改变 P(Y |V ) 的分布来生成不同的偏差数据。具体来说,通过偏差率 r∈ (0, 1) 的偏差样本选择来改变 P(Y |V ) 。对于每个样本,如果其噪声特征 V 等于结果变量 Y,则以概率 r 选择该样本,否则以概率 (1 - r ) 选择该样本。
YFCC100M [30]是一个大规模数据集,提供1亿张图像,每个图像包含多个标签。为了模拟各种非独立同分布。针对现实世界中的情况,作者构建了原始YFCC100M的子集,其中包括10个类别,并且类别中的图像被分为5个上下文。例如,在狗类别中,5 个上下文是草地、海滩、汽车、海洋和雪。为了便于可视化和解释,使用 SURF [4] 和 Bag-of-Words [6] 作为特征来表示图像。
WeChat Ads是2015年9月从腾讯微信App收集的真实在线广告数据集。对于每个广告,有两种类型的反馈:“喜欢”和“不喜欢”。该数据集包含 14,891 个喜欢和 93,108 个不喜欢的用户反馈。对于每个用户,有 56 个特征来描述他/她的个人资料,包括 (1) 人口统计属性,例如年龄、性别,(2) 朋友数量,(3) 设备(iOS 或 Android),以及 (4) 用户设置在微信应用程序上。很容易模拟针对一个或多个配置文件属性具有不同选择偏差的多个子集。
Office-Caltech 数据集 Office-Caltech 数据集收集了来自亚马逊、数码单反相机、网络摄像头和加州理工学院四个不同领域的图像,平均拥有近千张标记图像。由于不同的数据收集过程会产生偏差,因此 Office-Caltech 数据集在域适应领域得到了广泛应用 [32]。
4.2 Baselines
由于缺乏针对同一问题的直接相关研究,采用了几种基于相关性的经典算法和一种基于因果关系的两步算法来与 CRLR 进行比较。采用经典的逻辑回归(LR)作为最直接的基准,因为模型就是基于 LR 的。为了避免过度简化并获得更易解释的模型,还在逻辑回归(LR+L1)上施加了 L1 正则化,就像 Lasso [31] 所做的那样。还将 CRLR 与带线性核的支持向量机(SVM)和带 3 个隐藏层的多层感知器(MLP)进行了比较。此外,还采用了一种直截了当的两步解决方案(Two-Step),即首先通过混杂因素平衡[1]进行因果特征选择,然后应用逻辑回归。
通过对验证集进行交叉验证来调整算法和基线的参数。请注意,在图像分类实验中,省略了与基于 CNN 的图像分类器的比较,因为数据集中只有数千张图像,要从头开始训练一个 CNN 模型是不可行的。同时,由于非 i.i.d. 问题设置,无法使用预先训练好的深度模型(如 AlexNet),因为这些模型是用数百万张图像训练出来的,几乎涵盖了所有可能的文本。作者的目标是使用小规模或中等规模的训练数据来评估这些方法,因为非 i.i.d. 问题经常发生。
4.3 Experiments on Synthetic Data
在测试集上测试了不同偏差率(从 0.1 到 0.9)的算法,并计算了平均 RMSE 和标准误差。结果如图 2 所示。可以清楚地看到,在不同的训练设置下,逻辑回归的性能随着测试集上不同偏差率的变化而出现剧烈波动(标准误差较大),提出的方法则取得了相对更稳定、更准确的预测结果。这是因为 CRLR 利用了因果关系的稳定性,利用因果贡献而不是相关性进行预测。

4.4 Experiments on YFCC100M Dataset

相关文章:

论文阅读 - Causally Regularized Learning with Agnostic Data Selection
代码链接: GitHub - HMTTT/CRLR: CRLR尝试实现 https://arxiv.org/pdf/1708.06656v2 目录 摘要 INTRODUCTION 2 RELATED WORK 3 CAUSALLY REGULARIZED LOGISTIC REGRESSION 3.1 Problem Formulation 3.2 Confounder Balancing 3.3 Causally Regularized Lo…...

计算机网络之会话层
一、会话层的核心功能 会话层作为OSI模型的第五层,不仅承担着建立、管理和终止通信会话的基本任务,还隐含着许多复杂且关键的功能,这些功能共同确保了网络通信的高效、有序和安全。 1. 会话建立与连接管理: 身份验证与授权&…...

blind-watermark - 水印绑定
文章目录 一、关于 blind-watermark安装 二、bash 中使用三、Python 调用1、基本使用2、attacks on Watermarked Image3、embed images4、embed array of bits 四、并发五、相关 Project 一、关于 blind-watermark Blind watermark 基于 DWT-DCT-SVD. github : https://githu…...

reduce-scatter:适合分布式计算;Reduce、LayerNorm和Broadcast算子的执行顺序对计算结果的影响,以及它们对资源消耗的影响
目录 Gather Scatter Reduce reduce-scatter:适合分布式计算 Reduce、LayerNorm和Broadcast算子的执行顺序对计算结果的影响,以及它们对资源消耗的影响 计算结果理论正确性 资源消耗方面 Gather 这个也很好理解,就是把多个进程的数据拼凑在一起。 Scatter 不同于Br…...
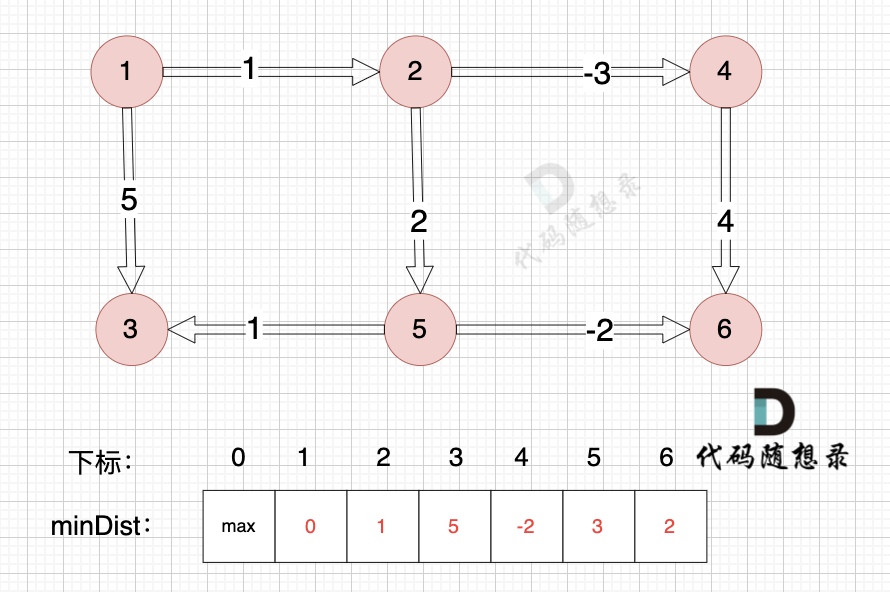
DAY64||dijkstra(堆优化版)精讲 ||Bellman_ford 算法精讲
dijkstra(堆优化版)精讲 题目如上题47. 参加科学大会(第六期模拟笔试) 邻接表 本题使用邻接表解决问题。 邻接表的优点: 对于稀疏图的存储,只需要存储边,空间利用率高遍历节点链接情况相对容…...

使用Git工具在GitHub的仓库中上传文件夹(超详细)
如何使用Git工具在GitHub的仓库中上传文件夹? 如果觉得博主写的还可以,点赞收藏关注噢~ 第一步:拥有一个本地的仓库 可以fork别人的仓库或者自己新创建 fork别人的仓库 或者自己创建一个仓库 按照要求填写完成后,点击按钮创建…...

Python酷库之旅-第三方库Pandas(218)
目录 一、用法精讲 1021、pandas.DatetimeIndex.inferred_freq属性 1021-1、语法 1021-2、参数 1021-3、功能 1021-4、返回值 1021-5、说明 1021-6、用法 1021-6-1、数据准备 1021-6-2、代码示例 1021-6-3、结果输出 1022、pandas.DatetimeIndex.indexer_at_time方…...

斗鱼大数据面试题及参考答案
MySQL 索引及引擎区别 一、MySQL 索引 索引是一种数据结构,用于快速查找数据库中的数据。它就像是一本书的目录,通过索引可以快速定位到需要的数据行,而不用全表扫描。 普通索引 普通索引是最基本的索引类型,它没有任何限制,可以在一个或多个列上创建。例如,在一个用户表…...

后仿真中的GLS测试用例的选取规则
一 仿真目的 门级仿真的主要目的,从根本上来说,是确保在物理实现阶段所应用的SDC(Standard Delay Constraint,标准延迟约束文件)中的各项约束条件准确无误地反映了设计的初衷和要求。这一环节在芯片设计的整体流程中占据着至关重要的地位,因为它直接关系到最终芯片的物理…...

对接阿里云实人认证
对接阿里云实人认证-身份二要素核验接口整理 目录 应用场景 接口文档 接口信息 请求参数 响应参数 调试 阿里云openApi平台调试 查看调用结果 查看SDK示例 下载SDK 遇到问题 本地调试 总结 应用场景 项目有一个提现的场景,需要用户真实的身份信息。 …...

UI库架构设计
UI库架构设计 分层 rc-xxx,提供基础组件,unstyled component (headless) ,只具备功能交互,不具备UI表现样式体系基础组件复合组件,Search:Input Select ,IconButton:Icon Button业…...

电子应用产品设计方案-9:全自动智能马桶系统设计方案
一、系统概述 本全自动智能马桶系统旨在提供舒适、卫生、便捷和智能化的如厕体验。通过融合多种传感器技术、电子控制单元和机械执行机构,实现马桶的自动冲洗、座圈加热、臀部清洗、烘干等功能,并具备智能感应、用户个性化设置和健康监测等特色功能。 二…...

My_SQL day3
知识点:约束 1.dafault 默认约束 2.not null 非空约束 3.unique key 唯一约束 4.primary key 主键约束 5.anto_increment 自增长约束 6.foreign key 外键约束 知识点:表关系 1.一对一 2.一对多 3.多对多 知识点:约束 1.default 默认约束 …...

【代码随想录day31】【C++复健】56. 合并区间;738.单调递增的数字
56. 合并区间 遇到了三个问题,一一说来: 1 比较应该按左区间排序,我却写了右区间。由于本题是合并区间,判断是否连续显然是用下一个的左区间与前一个的右区间比较,属于没想清楚了。 2 在写for循环时写成了如下的代码…...

jmeter常用配置元件介绍总结之逻辑控制器
系列文章目录 安装jmeter jmeter常用配置元件介绍总结之逻辑控制器 逻辑控制器1.IF控制器2.事务控制器3.循环控制器4.While控制器5.ForEach控制器6.Include控制器7.Runtime控制器8.临界部分控制器9.交替控制器10.仅一次控制器11.简单控制器12.随机控制器13.随机顺序控制器14.吞…...

解决Windows远程桌面 “为安全考虑,已锁定该用户账户,原因是登录尝试或密码更改尝试过多。请稍后片刻再重试,或与系统管理员或技术支持联系“问题
当我们远程连接服务器连接不上并提示“为安全考虑,已锁定该用户账户,原因是登录尝试或密码更改尝试过多。请稍候片刻再重试,或与系统管理员或技术支持联系”时,根本原因是当前计算机远程连接时输入了过多的错误密码,触…...

中文书籍对《人月神话》的引用(161-210本):微软的秘密
中文书籍对《人月神话》的引用(第001到160本)>> 《人月神话》于1975年出版,1995年出二十周年版。自出版以来,该书被大量的书籍和文章引用,直到现在热潮不退。 2023年,清华大学出版社推出《人月神话》…...

关于写React的一些反思和总结
这两个星期我都一直在写IT资产管理这个模块。关于这个模块,前端和后端都是我来处理,对于后端,我碰到了很多问题,但是很多问题都可以在比较短的时间内解决,而且不会说完全没有头绪的那种,这一方面源于我本身…...

Qt 每日面试题 -10
91、Qt设计界面有哪些方式? 手工编写创建界面的代码︰此方法比较复杂,不够直观;使用Qt Designer界面编辑器设计︰可直接拖放控件、设置控件的属性,简单、直观、易于操作;动态加载Ul文件并生成界面︰(QUiLoader类加载xx.ui)此方法很灵活,当需…...

三正科技笔试题
(15题,45分钟,闭卷) 一、( 8 分 )请问以下程序输出什么结果? char *getStr(void) 。 { char p[] "hellow world"; return p; } void test(void) { ch…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
