平衡二叉搜索树之 红黑 树的模拟实现【C++】
文章目录
- 红黑树的简单介绍
- 定义
- 红黑树的特性
- 红黑树的应用
- 全部的实现代码放在了文章末尾
- 准备工作
- 包含头文件
- 类的成员变量和红黑树节点的定义
- 构造函数和拷贝构造
- swap和赋值运算符重载
- 析构函数
- find
- insert【重要】
- 第一步:按照二叉搜索树的方式插入新节点
- 第二步:调整颜色,维护红黑树的规则
- 情况一:新插入的节点的父亲节点颜色为黑
- 情况二:新插入的节点的父亲节点颜色为红,且叔叔节点不为空且为红
- 情况三:新插入的节点的父亲节点颜色为红,且叔叔节点为空或者为黑
- empty
- size
- 中序遍历
- 红黑树和AVL树的比较
- 全部代码
红黑树的简单介绍
定义
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,只能是Red或Black。
通过对任何一条从根到空节点的路径上各个结点着色方式的限制
红黑树确保没有一条路径会比其他路径长出俩倍,即最长路径的长度最多是最短路径长度的两倍,这样的话就能保证红黑树是接近平衡的树

红黑树的特性
红黑树通过以下特性来保持树的平衡,保证最长路径的长度最多是最短路径长度的两倍:
-
节点颜色:每个节点只能是红色或黑色。
-
根节点:树的根节点是黑色。
-
红色规则:如果一个节点是红色,则它的两个子节点都是黑色(也就是说,一条路径
不能有两个连续的红色节点)。 -
黑色高度:从任一节点到其每个叶子的
所有简单路径都包含相同数目的黑色节点。 -
空节点:所有的空节点(NIL节点,通常是叶子节点的子节点)都是黑色。
为什么满足上面的特性,红黑树就能保证:最长路径的长度最多是最短路径长度的两倍呢?
其实很好理解
因为
特性2:根节点是黑的
特性4:每条路径的黑色节点个数是相同的
特性5:所有的空节点(NIL节点,通常是叶子节点的子节点)都是黑色。
那么任何一个红黑树可能出现的最短路径就是只有黑色节点的路径,因为每条路径的黑色节点个数是相同的
而任何一个红黑树可能出现的最长路径就是一黑一红交替的路径
为什么?
因为
特性1:每个节点只能是红色或黑色
特性3:每一条路径都不可能出现连续的红色节点
特性4:每条路径的黑色节点个数是相同的
所以最短路径和最长路径的黑色节点个数一样
所以最长也只能是黑红节点交替出现
因此
可能的最短的路径,是全黑节点
可能的最长路径是一黑一红,交替出现的路径,红黑节点个数相同
所以
如果全黑节点的路径长度为h
那么一黑一红交替出现的路径长度最多只能是2*h
红黑树的应用
红黑树是一种高效的自平衡二叉搜索树,因其出色的性能和良好的平衡特性,在计算机科学中被广泛应用。以下是红黑树的一些主要应用场景:
-
Java 和 C++ 中的集合和数据结构:
- 在 Java 中,红黑树被用于实现
TreeSet和TreeMap,分别提供有序集合和有序映射的功能。 - 在 C++ 中,红黑树是
std::set、std::multiset、std::map和std::multimap的底层数据结构。
- 在 Java 中,红黑树被用于实现
-
数据库索引:
- 红黑树常用于数据库系统中,作为索引结构来提高数据查询和更新的效率。
通过维持数据的有序性和快速搜索特性,红黑树能够有效地管理大量数据。
- 红黑树常用于数据库系统中,作为索引结构来提高数据查询和更新的效率。
-
操作系统的内存管理:
- 在操作系统中,红黑树可用于管理内存分配。例如,在 Linux 的虚拟内存管理中,红黑树被用来维护页面分配的信息,确保内存的高效使用。
-
文件系统和文件管理:
- 在文件系统中,红黑树可以用来存储文件元数据,比如文件名、大小和修改时间等信息,以便快速检索和排序。
-
网络协议和算法:
- 在一些网络协议的实现中,红黑树可以用来管理连接状态或路由表,以实现高效的数据包转发和路由决策。
-
图形渲染和游戏开发:
- 在图形渲染和游戏开发中,红黑树可用于管理场景中的物体,通过快速搜索和排序来优化渲染列表。
-
科学计算和数据分析:
- 在科学计算和数据分析中,红黑树可以用于管理大量的有序数据,提供快速的搜索和更新操作,这对于时间序列数据的处理尤为重要。
红黑树可以确保数据结构的稳定性和效率,对于处理大量动态变化的数据集合尤为重要。
全部的实现代码放在了文章末尾
准备工作
创建两个文件,一个头文件RBTree.hpp,一个源文件test.cpp
【因为模板的声明和定义不能分处于不同的文件中,所以把成员函数的声明和定义放在了同一个文件RBTree.hpp中】
-
RBTee.hpp:存放包含的头文件,命名空间的定义,成员函数和命名空间中的函数的定义
-
test.cpp:存放main函数,以及测试代码
包含头文件
- iostream:用于输入输出
- cmath:提供数学函数
类的成员变量和红黑树节点的定义
红黑树类的成员变量只有一个,就是指向红黑树的根节点的指针

红黑树的节点类:

为什么红黑树新插入的节点【或者新节点】一定是红色的?
其实就是维护成本的问题:
1.如果新插入的节点为黑色
因为插入之前,这棵树一定是红黑树
所以他的每一条路径上的黑色节点个数都相同
但是因为你新插入了一个黑色的,这一条路径就会比其他路径多一个黑色节点,为了保持红黑树的规则(每一条路径上的黑色节点个数都相同)
就得想办法让每一条路径也都增加一个黑色节点,维护成本太高了
2.如果新插入的节点为红色
① 新插入的节点的父亲为黑色,就可以直接结束了,因为满足红黑树的所有规则
②就算新插入的节点的父亲为红色,调整的情况也只有两种,维护成本更低
构造函数和拷贝构造
构造函数没什么好说的,默认构造就行了
RBTree() :_root(nullptr)
{}
拷贝构造:
因为节点都是从堆区new出来的,所以要深拷贝
使用递归实现深拷贝:
因为拷贝构造不能有多余的参数,但是递归函数又必须使用参数记录信息

然后在拷贝构造里面调用一下这个函数就行了
RBTree(const RBTree& obj)
{_root = Copy(obj._root, nullptr);
}swap和赋值运算符重载
交换两颗红黑树的本质就是交换两颗数的资源(数据),而它们的资源都是从堆区申请来的,然后用指针指向这些资源

并不是把资源存储在了红黑树对象中
所以资源交换很简单,直接交换_root指针的指向即可
void Swap(RBTree& obj)
{std::swap(_root, obj._root);
}
赋值运算符重载
RBTree& operator=(RBTree obj)
{this->Swap(obj);return *this;
}
为什么上面的两句代码就可以完成深拷贝呢?
这是因为:
使用了传值传参,会在传参之前调用拷贝构造,再把拷贝构造出的临时对象作为参数传递进去
赋值运算符的左操作数,*this再与传入的临时对象obj交换,就直接完成了拷贝
在函数结束之后,存储在栈区的obj再函数结束之后,obj生命周期结束
obj调用析构函数,把指向的从*this那里交换来的不需要的空间销毁
析构函数
使用递归遍历,把所有从堆区申请的节点都释放掉:
因为析构函数不能有多余的参数,但是递归函数又必须使用参数记录信息
所以再封装一个成员函数,专门用来递归释放:

然后在拷贝构造里面调用一下这个函数就行了
~RBTree()
{Destroy(_root);_root = nullptr;
}
find
具体流程:
从根节点开始,将目标值(传入的key)与当前节点的key进行比较。
如果目标值小于当前节点值,则在左子树中继续查找;
如果目标值大于当前节点值,则在右子树中继续查找。
这个过程一直进行,直到找到与目标值或者到达空节点为止。
把上述过程转成代码:

insert【重要】
红黑树就是在二叉搜索树的基础上节点有了颜色,因此红黑树也可以看成是二叉搜索树。
那么AVL树的插入过程可以分为两步:
-
先按照二叉搜索树的方式插入新节点
-
再调整颜色,维护红黑树的规则
第一步:按照二叉搜索树的方式插入新节点
插入的具体过程如下:
-
树为空,则直接新增节点,赋值给二叉搜索树的成员变量
_root指针 -
树不空,则按照查找(
find)的逻辑找到新节点应该插入的位置 -
树不空,如果树中已经有了一个节点的key值与要插入的节点的key相同,就插入失败
这个过程一直进行,直到找到与传入的key相等的节点或者到达空节点为止。
把上述过程转成代码:

第二步:调整颜色,维护红黑树的规则
颜色调整分以下3种情况:
- 新插入的节点(cur)的父亲节点(parent)颜色为
黑 - 新插入的节点(cur)的父亲节点(parent)颜色为
红,且叔叔(uncle)节点不为空且为红 - 新插入的节点(cur)的父亲节点(parent)颜色为
红,且叔叔(uncle)节点为空或者为黑
情况一:新插入的节点的父亲节点颜色为黑
此时插入节点,并没有违反任何红黑树规则,所以不需要调整颜色/树的结构
直接结束插入就行
情况二:新插入的节点的父亲节点颜色为红,且叔叔节点不为空且为红

(cur为新插入的节点,g是爷爷节点,u是父亲的兄弟节点;a,b,c,d,e是都是符合条件的红黑树)
cur的位置是不固定的
cur也可以是上图的c,d,e
cur的p,g,u相应的改变即可
最主要看的是cur和它的g,p,u的颜色,是否满足情况一
因为插入的节点的颜色为红色,而且它的父亲节点也是红色
那么它就违反了红黑树的第3条规则:同一路径不能出现连续的红色节点
所以必须进行调整。
因为叔叔节点不为空且为红,所以没有严重违反红黑树的规则,只需要对颜色进行调整即可
所以调整方案是:
①把p,u都变黑,把g变红:这样就能让连续的红色节点去除,但是g(爷爷接节点)变成红色了,g的父亲节点也可能是红色
所以需要
②再把g看作cur继续循环向上调整,再根据新的c,p,u,g节点的颜色,判断是情况一,情况二还是情况三
具体实现代码:

情况三:新插入的节点的父亲节点颜色为红,且叔叔节点为空或者为黑

【此时cur的位置也是不固定的
cur也可以是上图的c,d,e
cur的p,g,u相应的改变即可
最主要看的是cur和它的g,p,u的颜色,是否满足情况二】
因为插入的节点的颜色为红色,而且它的父亲节点也是红色
那么它就违反了红黑树的第3条规则:同一路径不能出现连续的红色节点
所以必须进行调整。
因为叔叔(uncle)节点为空或者为黑,所以严重违反红黑树的规则,需要调整红黑树的部分结构和调整颜色
所以此时的调整方案是:
先旋转[根据cur,p和g的相对位置,进行左旋,右旋,双旋],再变颜色
【如果不知道旋转是什么的话,可以看我这篇文章:平衡二叉搜索树之 AVL 树的模拟实现【C++】中的怎么旋转】
①单旋:p变黑,g变红
因为单旋之后, p就变成了c,p,g及其子树组成的这棵树的根节点
然后又因为g是黑色,所以他旋转下去的话,
那么c那条路径就会比其他路径少一个黑色节点
所以需要把作为新的根节点的p变黑,这样c那条路径的黑色节点数量才会与其他路径上的相同
但是这样又会让g那条路径比其他的路径多一个黑色节点
所以再把g变红

②双旋:c变黑,g变红
因为单旋之后, c就变成了c,p,g及其子树组成的这棵树的根节点
然后的推导就与单旋的类似了
具体代码实现:



empty
bool Empty()
{如果_root为空,那么树就是空的return _root == nullptr;
}
size
使用递归实现二叉搜索树的节点个数统计:
因为我们经常使用的stl的容器的size都是没有参数的,但是递归函数又必须使用参数记录信息
所以再封装一个成员函数,专门用来递归:

然后再size里面调用一下就行了
size_t Size()
{return _Size(_root);
}
中序遍历
中序遍历的递归函数:

然后再调用递归函数
void InOrder()
{_InOrder(_root);
}
红黑树和AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O( l o g 2 N log_2 N log2N)
红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,减少了旋转的次数
所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单
所以实际运用中红黑树更多
全部代码
#define _CRT_SECURE_NO_WARNINGS#include<iostream>
#include<cmath>
using namespace std;//定义枚举,枚举节点的颜色
enum Color
{RED,//红色BLACK//黑色
};template<class T>
struct RBTreeNode
{T _data;//节点中存储的数据RBTreeNode* _parent;//指向节点的父亲节点RBTreeNode* _left;//指向节点的左孩子RBTreeNode* _right;//指向节点的右孩子Color _color;//存储节点的颜色//默认构造RBTreeNode(const T& data = T()):_data(data),_parent(nullptr),_left(nullptr),_right(nullptr),_color(RED)//新节点的颜色默认是红色{}
};//模板参数T,就是节点中存储的数据的类型
template<class T>
class RBTree
{//给节点类重命名typedef RBTreeNode<T> Node;
private://指向红黑树的根节点的指针Node* _root = nullptr;public:RBTree():_root(nullptr){}RBTree(const RBTree& obj){_root = Copy(obj._root, nullptr);}RBTree& operator=(RBTree obj){this->Swap(obj);return *this;}~RBTree(){Destroy(_root);_root = nullptr;}void Swap(RBTree& obj){std::swap(_root, obj._root);}bool Insert(const T& data){Node* newnode = new Node(data);if (_root == nullptr){_root = newnode;_root->_color = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_data < data){parent = cur;cur = cur->_right;}else if (cur->_data > data){parent = cur;cur = cur->_left;}else{return false;}}if (parent->_data > data){parent->_left = newnode;}else{parent->_right = newnode;}newnode->_parent = parent;cur = newnode;//如果新插入的节点的父节点的颜色是 黑色// 因为已经符合红黑树的规则了,直接结束插入if (parent->_color == BLACK)return true;//直接结束else//否则{Node* grandpa = parent->_parent;//爷爷节点Node* uncle = nullptr;//叔叔节点,即cur的父亲节点的 兄弟节点if (parent == grandpa->_left)//如果parent是左孩子{uncle = grandpa->_right;//那么它的兄弟节点就是右孩子}else//如果parent是右孩子{uncle = grandpa->_left;//那么它的兄弟节点就是左孩子}//情况二:// cur的父亲节点(parent)为红,且叔叔(uncle)节点不为空且为红//只需要继续 循环 向上调整while (parent->_color == RED && uncle && uncle->_color == RED){//调整颜色grandpa->_color = RED;parent->_color = BLACK;uncle->_color = BLACK;//如果调整到根节点,就不需要再向上调整了if (grandpa == _root){//因为根节点只能是黑色//所以把爷爷节点(grandpa)的颜色调成黑色grandpa->_color = BLACK;return true;//直接结束}//重新赋值//继续向上调整cur = grandpa;//让原来的爷爷节点作为curparent = cur->_parent;//重新得出新的父亲节点//如果新的父亲节点为黑,就和刚插入节点时一样// 因为已经符合红黑树的规则了,直接结束插入if (parent->_color == BLACK)return true;//直接结束grandpa = parent->_parent;//重新得出新的爷爷节点//重新得出新的叔叔节点if (parent == grandpa->_left){uncle = grandpa->_right;}else{uncle = grandpa->_left;}}//情况三:// cur的父亲节点(parent)为红,且叔叔(uncle)节点为空或者为黑//就只能根据情况,旋转处理一次if (parent->_color == RED&&uncle == nullptr || uncle->_color == BLACK){if (parent == grandpa->_right && cur == parent->_right)//左单旋{RotateL(grandpa);//调整颜色parent->_color = BLACK;grandpa->_color = RED;}else if (parent == grandpa->_left && cur == parent->_left)//右单旋{RotateR(grandpa);//调整颜色parent->_color = BLACK;grandpa->_color = RED;}else if (parent == grandpa->_left && cur == parent->_right)//左右双旋{RotateL(parent);RotateR(grandpa);//调整颜色cur->_color = BLACK;grandpa->_color = RED;}else if (parent == grandpa->_right && cur == parent->_left)//右左双旋{RotateR(parent);RotateL(grandpa);//调整颜色cur->_color = BLACK;grandpa->_color = RED;}}}return true;}Node* Find(const T& data){Node* cur = _root;while (cur){if (cur->_data < data){cur = cur->_right;}else if (cur->_data > data){cur = cur->_left;}else{return cur;}}return nullptr;}void InOrder(){_InOrder(_root);cout << endl;}bool Empty(){return _root == nullptr;}size_t Size(){return _Size(_root);}size_t Height(){return _Height(_root);}bool IsRBTree(){if (_root == nullptr)return true;if (_root->_color != BLACK)return false;int count = 0;Node* cur = _root;while (cur){if (cur->_color == BLACK)count++;cur = cur->_left;}return _IsRBTree(_root, count, 0);}
private:bool _IsRBTree(const Node* root, const int& total, int count){if (root == nullptr){if (count != total)return false;elsereturn true;}if (root->_color == RED && root->_parent->_color == RED)return false;if (root->_color == BLACK)count++;if (_IsRBTree(root->_left, total, count) == false)return false;if (_IsRBTree(root->_right, total, count) == false)return false;return true;}size_t _Height(Node* root){if (root == nullptr)return 0;int left = _Height(root->_left);int right = _Height(root->_right);return left > right ? left + 1 : right + 1;}// 左单旋void RotateL(Node* parent){//记录一下PR和PRLNode* PR = parent->_right;Node* PRL = PR->_left;//把PRL链接在parent的右边parent->_right = PRL;//因为PRL可能为空,为了防止空指针访问,必须判断一下if (PRL != nullptr){//PRL不为空,就把它的父亲节点变成parentPRL->_parent = parent;}//把parent链接在PR的左边PR->_left = parent;//更改PR的父亲节点PR->_parent = parent->_parent;//只有AVL树的根节点的父亲节点为空//所以parent是根节点if (parent->_parent == nullptr){//PR变成了这颗子树的根,替代了原来parent的位置//所以得把AVL树的根节点更新一下_root = PR;}else//如果parent不是根节点{//PR还是要带替parent的位置//所以parent在父亲的左,PR就在左//parent在父亲的右,PR就在右if (parent == parent->_parent->_left)parent->_parent->_left = PR;elseparent->_parent->_right = PR;}//更新一下parent的父亲节点parent->_parent = PR;}// 右单旋void RotateR(Node* parent){//记录一下PL和PLRNode* PL = parent->_left;Node* PLR = PL->_right;//把PLR链接在parent的右边parent->_left = PLR;//因为PLR可能为空,为了防止空指针访问,必须判断一下if (PLR != nullptr){//不为空,就把它的父亲节点变成parentPLR->_parent = parent;}//把parent链接在PL的左边PL->_right = parent;//更新PL的父亲节点PL->_parent = parent->_parent;//只有AVL树的根节点的父亲节点为空//所以parent是根节点if (parent->_parent == nullptr){//PL变成了这颗子树的根,替代了原来parent的位置//所以得把AVL树的根节点更新一下_root = PL;}else//如果parent不是根节点{//PL还是要带替parent的位置//所以parent在父亲的左,PL就在左//parent在父亲的右,PL就在右if (parent == parent->_parent->_left)parent->_parent->_left = PL;elseparent->_parent->_right = PL;}//更新一下parent的父亲节点parent->_parent = PL;}//因为无法直接获取到父亲节点的地址//所以需要传参传进来Node* Copy(Node* root, Node* parent){//空节点不需要拷贝,直接返回nullptrif (root == nullptr)return nullptr;//从堆区申请空间,并初始化节点Node* newnode = new Node(root->_data);//连接上传入函数的父亲节点newnode->_parent = parent;//拷贝颜色newnode->_color = root->_color;//递归拷贝左右子树newnode->_left = Copy(root->_left, newnode);newnode->_right = Copy(root->_right, newnode);return newnode;//返回新节点}//使用后序遍历进行释放void Destroy(Node* root){//空节点if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_data << " ";_InOrder(root->_right);}size_t _Size(Node* root){if (root == nullptr)return 0;int left = _Size(root->_left);int right = _Size(root->_right);return left + right + 1;}
};相关文章:

平衡二叉搜索树之 红黑 树的模拟实现【C++】
文章目录 红黑树的简单介绍定义红黑树的特性红黑树的应用 全部的实现代码放在了文章末尾准备工作包含头文件类的成员变量和红黑树节点的定义 构造函数和拷贝构造swap和赋值运算符重载析构函数findinsert【重要】第一步:按照二叉搜索树的方式插入新节点第二步&#x…...

2:Vue.js 父子组件通信:让你的组件“说话”
上一篇我们聊了如何用 Vue.js 创建一个简单的组件,这次咱们再往前走一步,讲讲 Vue.js 的父子组件通信。组件开发里,最重要的就是让组件之间能够“说话”,数据能流通起来。废话不多说,直接开干! 父组件传数据…...

6. Keepalived配置Nginx自动重启,实现7x24提供服务
一. Keepalived配置Nginx自动重启,实现7x24提供服务 1.编写不停的检查nginx服务器状态,停止并重启,重启失败后则停止keepalived脚本 cd /etc/keepalived/ vim check_nginx_alive_or_not.sh #---内容如下:--------------- #!/bin/bash A=`ps -C nginx --no-header |wc -l...

【PS】蒙版与通道
内容1: 、选择蓝色通道并复制,对复制的蓝色通道ctrli进行反向选择,然后ctrll调整色阶。 、选择载入选区,然后点击rgb。 、点击蒙版 、点击云彩图层调整位置 、点击色相/饱和度,适当调整 、最后使用滤镜等功能添加光圈…...

C++创建型模式之生成器模式
解决的问题 生成器模式(Builder Pattern)主要解决复杂对象的构建问题。当一个对象的创建过程非常复杂,涉及多个步骤和多个部件时,使用生成器模式可以将对象的构建过程与其表示分离,使得同样的构建过程可以创建不同的表…...

鸿蒙NEXT应用示例:切换图片动画
【引言】 在鸿蒙NEXT应用开发中,实现图片切换动画是一项常见的需求。本文将介绍如何使用鸿蒙应用框架中的组件和动画功能,实现不同类型的图片切换动画效果。 【环境准备】 电脑系统:windows 10 开发工具:DevEco Studio NEXT B…...
继承特性和分区实现)
postgresql(功能最强大的开源数据库)继承特性和分区实现
PostgreSQL实现了表继承,在多重表继承下,对上亿条不同类别的数据条目进行按型号、按月份双层分区管理,既可在总表查阅所有条目的共有字段,也可在各类型字表查询附加字段,非常高效。 分区是通过继承的方式来实现的&…...
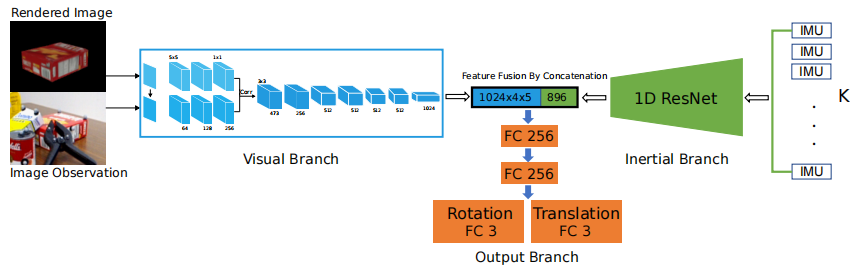
论文笔记(五十六)VIPose: Real-time Visual-Inertial 6D Object Pose Tracking
VIPose: Real-time Visual-Inertial 6D Object Pose Tracking 文章概括摘要I. INTRODACTIONII. 相关工作III. APPROACHA. 姿态跟踪工作流程B. VIPose网络 文章概括 引用: inproceedings{ge2021vipose,title{Vipose: Real-time visual-inertial 6d object pose tra…...

微服务治理详解
文章目录 什么是微服务架构为什么要使用微服务单体架构如何转向微服务架构服务治理服务治理治的是什么服务注册与发现服务熔断降级服务网关服务调用服务负载均衡服务配置中心 微服务解决方案SpringCloud体系EurekaHystrixGatewayOpenFeignRibbonConfig SpringCloud Alibaba体系…...
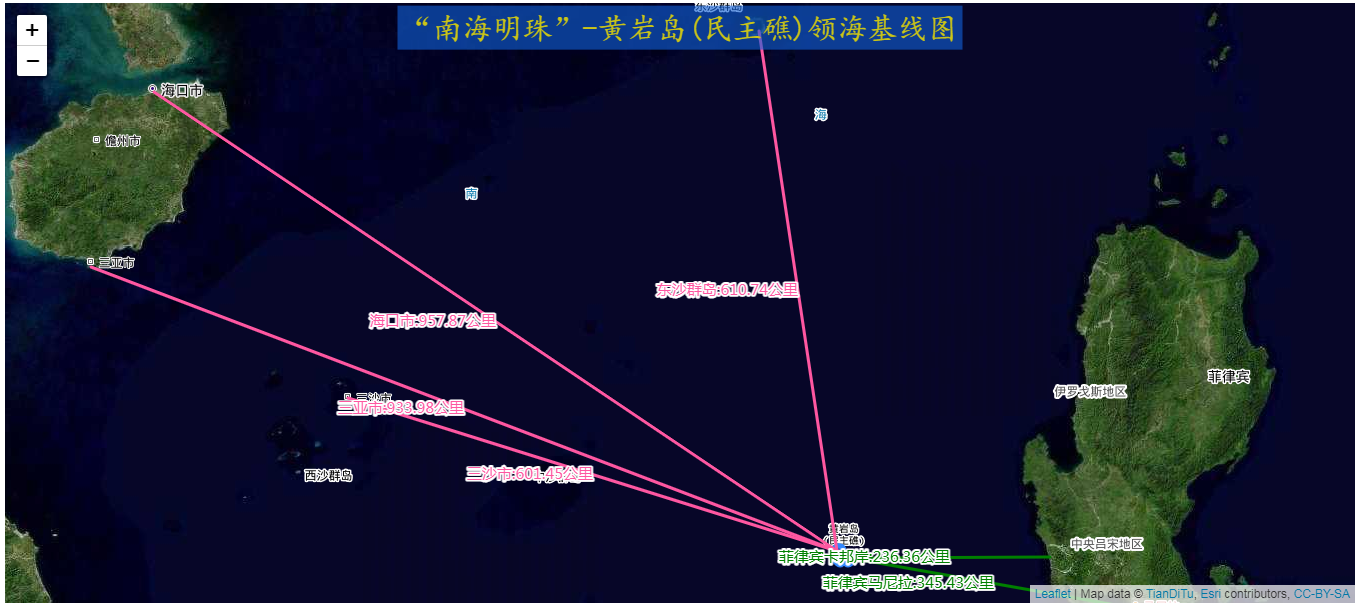
“南海明珠”-黄岩岛(民主礁)领海基线WebGIS绘制实战
目录 前言 一、关于岛屿的基点位置 1、领海基点 二、基点坐标的转换 1、最底层的左边转换 2、单个经纬度坐标点转换 3、完整的转换 三、基于天地图进行WebGIS展示 1、领海基点的可视化 2、重要城市距离计算 四、总结 前言 南海明珠黄岩岛,这座位于南海的…...

Oracle数据库 创建dblink的过程及其用法详解
前言 dblink是Oracle数据库中用于连接不同数据库实例的一种机制。通过dblink,用户可以在一个数据库实例中直接查询或操作另一个数据库实例中的表、视图或存储过程。 dblink的作用主要体现在以下几个方面: 跨数据库操作:允许用户…...

Linux从0——1之shell编程4
声明! 学习视频来自B站up主 **泷羽sec** 有兴趣的师傅可以关注一下,如涉及侵权马上删除文章,笔记只是方便各位师傅的学习和探讨,文章所提到的网站以及内容,只做学习交流,其他均与本人以及泷羽sec团队无关&a…...

pycharm快速更换虚拟环境
目录 1. 选择Conda 虚拟环境2. 创建环境3. 直接选择现有虚拟环境 1. 选择Conda 虚拟环境 2. 创建环境 3. 直接选择现有虚拟环境...

MVVM框架
MVVM由以下三个内容构成: Model:数据模型View:界面ViewModel:作为桥梁负责沟通View和Model 在JQuery时期,如果需要刷新UI,需要先取到对应的 DOM 再更新 UI,这样数据和业务的逻辑就和⻚⾯有强耦合。 在 MVVM 中,UI 是…...

数据仓库在大数据处理中的作用
数据仓库(Data Warehouse,简称DW或DWH)是一个面向主题的、集成的、相对稳定的、反映历史变化的数据集合,用于支持管理决策。以下是对数据仓库及其在大数据处理中作用的详细解释: 一、数据仓库的定义 面向主题&#x…...
)
前端Javascript、Vue、CSS等场景面试题目(二)
前端面试场景题目(一)-CSDN博客 针对您提供的前端场景面试题目,以下是详细的回答: 1. 如何通过 CSS 实现美观的自定义复选框和单选按钮? 方法:使用 CSS 伪元素 ::before 和 ::after,以及隐藏…...
)
鸿蒙学习生态应用开发能力全景图-开发者支持平台(5)
鸿蒙相关平台作用: 开发者社区:开发者技术交流平台,帮助开发者探索开发实践、交流心得经验、获悉业界动态、答疑解惑。 开发者学堂:聚合官方鸿蒙生态课程,课程有慕课、微课、直播课、训练营等多种形式ÿ…...

计算机网络各层设备总结归纳(更新ing)
计算机网络按照OSI(开放式系统互联)模型分为七层,每一层都有其特定的功能和对应的网络设备。以下是各层对应的设备: 1. 物理层(Physical Layer) 设备:中继器(Repeater)、集线器…...

3. Spring Cloud Eureka 服务注册与发现(超详细说明及使用)
3. Spring Cloud Eureka 服务注册与发现(超详细说明及使用) 文章目录 3. Spring Cloud Eureka 服务注册与发现(超详细说明及使用)前言1. Spring Cloud Eureka 的概述1.1 服务治理概述1.2 服务注册与发现 2. 实践:创建单机 Eureka Server 注册中心2.1 需求说明 图解…...
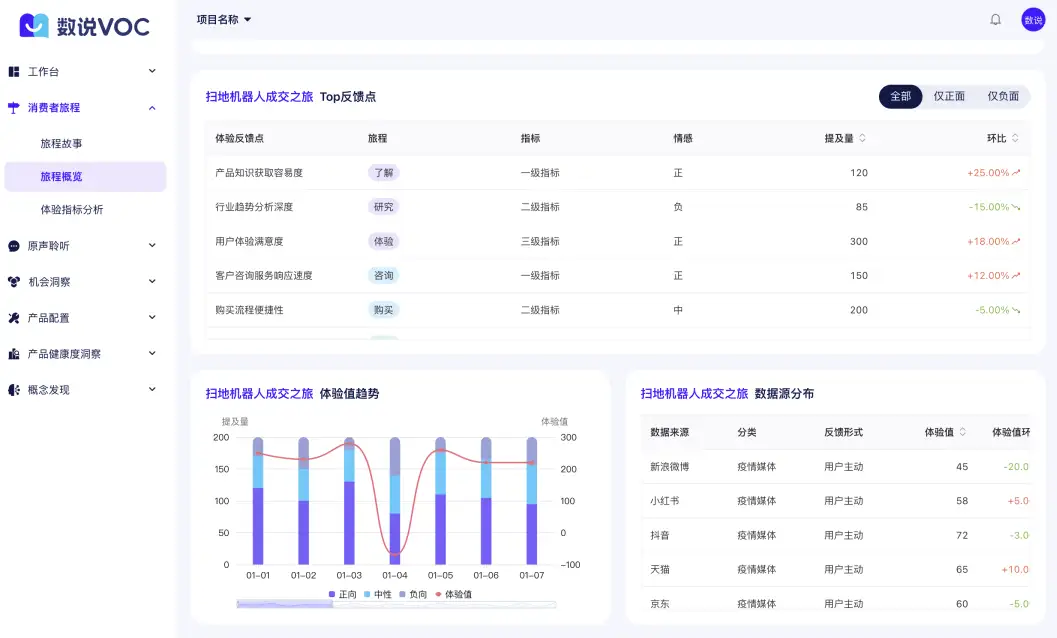
品牌如何利用大数据工具,进行消费者洞察分析?
存量竞争的时代, 消费者聆听是品牌持续增长的关键,借助大数据的消费者数据洞察,可以帮助品牌分析消费者的所思所想及行为特征,获取消费者对产品的需求痛点、使用感受,对品牌的评价口碑等,从而帮助品牌更好地…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
