树状数组+概率论,ABC380G - Another Shuffle Window
目录
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
二、解题报告
1、思路分析
2、复杂度
3、代码详解
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
G - Another Shuffle Window
二、解题报告
1、思路分析
不难用树状数组计算全局逆序对tot
我们可以在滑窗过程中维护当前 k-子数组的逆序对数目cur(不计入滑窗内的数和滑窗外的数字构成的逆序对)
对于滑窗的每个时刻,滑窗外元素对逆序对的贡献为 tot - cur
也就是说,每个滑窗,不带滑窗内会有tot - cur个逆序对
每个滑窗这一部分的贡献为 (tot - cur) * (n - k + 1),因为 n - k + 1个滑窗等概率,所以贡献比例相同,这一部分的答案我们滑窗过程中直接累加
关键在于如何理解滑窗内元素之间的逆序对数目?
我们发现我们只需计算子数组内产生的逆序对,而对于一个数组而言,数组内任意两个数之间构成逆序对的数目为 1 / 2,而 k-数组 pair 的数目为 k * (k - 1) / 2,每个pair 贡献1个逆序对的概率为1/2,根据二项分布的数学期望计算公式:E = np可得,k-数组的逆序对贡献期望为 k * (k - 1) / 4
那么答案就是把两部分加起来,详细看代码
2、复杂度
时间复杂度: O(NlogN)空间复杂度:O(N)
3、代码详解
#include <bits/stdc++.h>// #define DEBUGusing u32 = unsigned;
using i64 = long long;
using u64 = unsigned long long;constexpr int inf32 = 1E9 + 7;
constexpr i64 inf64 = 1E18 + 7;template<class T>
constexpr T power(T a, i64 b) {T res = 1;for (; b; b /= 2, a *= a) {if (b % 2) {res *= a;}}return res;
}constexpr i64 mul(i64 a, i64 b, i64 p) {i64 res = a * b - i64(1.L * a * b / p) * p;res %= p;if (res < 0) {res += p;}return res;
}
template<i64 P>
struct MLong {i64 x;constexpr MLong() : x{} {}constexpr MLong(i64 x) : x{norm(x % getMod())} {}static i64 Mod;constexpr static i64 getMod() {if (P > 0) {return P;} else {return Mod;}}constexpr static void setMod(i64 Mod_) {Mod = Mod_;}constexpr i64 norm(i64 x) const {if (x < 0) {x += getMod();}if (x >= getMod()) {x -= getMod();}return x;}constexpr i64 val() const {return x;}explicit constexpr operator i64() const {return x;}constexpr MLong operator-() const {MLong res;res.x = norm(getMod() - x);return res;}constexpr MLong inv() const {assert(x != 0);return power(*this, getMod() - 2);}constexpr MLong &operator*=(MLong rhs) & {x = mul(x, rhs.x, getMod());return *this;}constexpr MLong &operator+=(MLong rhs) & {x = norm(x + rhs.x);return *this;}constexpr MLong &operator-=(MLong rhs) & {x = norm(x - rhs.x);return *this;}constexpr MLong &operator/=(MLong rhs) & {return *this *= rhs.inv();}friend constexpr MLong operator*(MLong lhs, MLong rhs) {MLong res = lhs;res *= rhs;return res;}friend constexpr MLong operator+(MLong lhs, MLong rhs) {MLong res = lhs;res += rhs;return res;}friend constexpr MLong operator-(MLong lhs, MLong rhs) {MLong res = lhs;res -= rhs;return res;}friend constexpr MLong operator/(MLong lhs, MLong rhs) {MLong res = lhs;res /= rhs;return res;}friend constexpr std::istream &operator>>(std::istream &is, MLong &a) {i64 v;is >> v;a = MLong(v);return is;}friend constexpr std::ostream &operator<<(std::ostream &os, const MLong &a) {return os << a.val();}friend constexpr bool operator==(MLong lhs, MLong rhs) {return lhs.val() == rhs.val();}friend constexpr bool operator!=(MLong lhs, MLong rhs) {return lhs.val() != rhs.val();}
};template<>
i64 MLong<0LL>::Mod = i64(1E18) + 9;template<int P>
struct MInt {int x;constexpr MInt() : x{} {}constexpr MInt(i64 x) : x{norm(x % getMod())} {}static int Mod;constexpr static int getMod() {if (P > 0) {return P;} else {return Mod;}}constexpr static void setMod(int Mod_) {Mod = Mod_;}constexpr int norm(int x) const {if (x < 0) {x += getMod();}if (x >= getMod()) {x -= getMod();}return x;}constexpr int val() const {return x;}explicit constexpr operator int() const {return x;}constexpr MInt operator-() const {MInt res;res.x = norm(getMod() - x);return res;}constexpr MInt inv() const {assert(x != 0);return power(*this, getMod() - 2);}constexpr MInt &operator*=(MInt rhs) & {x = 1LL * x * rhs.x % getMod();return *this;}constexpr MInt &operator+=(MInt rhs) & {x = norm(x + rhs.x);return *this;}constexpr MInt &operator-=(MInt rhs) & {x = norm(x - rhs.x);return *this;}constexpr MInt &operator/=(MInt rhs) & {return *this *= rhs.inv();}friend constexpr MInt operator*(MInt lhs, MInt rhs) {MInt res = lhs;res *= rhs;return res;}friend constexpr MInt operator+(MInt lhs, MInt rhs) {MInt res = lhs;res += rhs;return res;}friend constexpr MInt operator-(MInt lhs, MInt rhs) {MInt res = lhs;res -= rhs;return res;}friend constexpr MInt operator/(MInt lhs, MInt rhs) {MInt res = lhs;res /= rhs;return res;}friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {i64 v;is >> v;a = MInt(v);return is;}friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {return os << a.val();}friend constexpr bool operator==(MInt lhs, MInt rhs) {return lhs.val() == rhs.val();}friend constexpr bool operator!=(MInt lhs, MInt rhs) {return lhs.val() != rhs.val();}
};template<>
int MInt<0>::Mod = 998244353;template<int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();constexpr int P = 998244353;
using Z = MInt<P>;template<typename T>
class FenWick {
private:int n;std::vector<T> tr;
public:FenWick(int _n) : n(_n), tr(_n + 1) {}FenWick(const std::vector<T> &_init) : FenWick(_init.size()) {init(_init);}void init(const std::vector<T> &_init) {for (int i = 1; i <= n; ++ i) {tr[i] += _init[i - 1];int j = i + (i & -i);if (j <= n)tr[j] += tr[i];}}void add(int x, int k) {for (; x <= n; x += x & -x) tr[x] += k;}void add(int l, int r, T k) {add(l, k);if (r + 1 <= n)add(r + 1, -k);}T query(int x) const {T res = T{};for (; x; x &= x - 1) { res += tr[x];}return res;}T query(int l, int r) const {if (l > r) return T{};return query(r) - query(l - 1);}int select(int k) {int x = 0;T cur{};for (int i = 1 << std::__lg(n); i; i /= 2) {if (x + i <= n && cur + tr[x + i] < k) {x += i;cur = cur + tr[x];}}return x + 1;}void clear() {tr.assign(n + 1, T{});}
};void solve() {int n, k;std::cin >> n >> k;std::vector<int> p(n);for (int i = 0; i < n; ++ i) {std::cin >> p[i];}FenWick<Z> fen(n);Z tot = 0;for (int i = n - 1; ~i; -- i) {tot += fen.query(p[i]);fen.add(p[i], 1);}fen.clear();Z cur = 0;for (int i = k - 1; ~i; -- i) {cur += fen.query(p[i]);fen.add(p[i], 1);}Z ans = tot - cur;for (int i = 0; i + k < n; ++ i) {fen.add(p[i], -1);cur -= fen.query(p[i]);cur += fen.query(p[i + k], n);fen.add(p[i + k], 1);ans += tot - cur;}std::cout << (ans * Z(n - k + 1).inv() + Z(4).inv() * Z(k) * Z(k - 1)) << '\n';
}int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);#ifdef DEBUGint START = clock();freopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);
#endifint t = 1;// std::cin >> t;while (t --) {solve();}
#ifdef DEBUGstd::cerr << "run-time: " << clock() - START << '\n';
#endifreturn 0;
}相关文章:

树状数组+概率论,ABC380G - Another Shuffle Window
目录 一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 二、解题报告 1、思路分析 2、复杂度 3、代码详解 一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 G - Another Shuffle Window 二、解题报告 1、思路分析 不难用树状数组计…...

机器学习day1-数据集
机器学习 一、机器学习 1.定义 让计算机在数据中学习规律并根据得到的规律对未来进行预测。 2.发展史 19世纪50年代:图灵测试提出、塞缪尔开发的西洋跳棋程序,标志着机器学习正式进入发展期 19世纪80年代:神经网络反向传播(…...

【Golang】——Gin 框架中的路由与请求处理
文章目录 1. 路由基础1.1 什么是路由?1.2 Gin 中的路由概述 2. 创建简单路由2.1 基本路由定义2.2 不同请求方法的路由 3. 路由参数3.1 路径参数3.2 查询参数 4. 路由分组4.1 为什么使用路由分组?4.2 路由分组示例 5. 请求处理与响应5.1 Gin 中的 Context…...

nuxt3添加wowjs动效
1、安装wowjs pnpm i wowjs1.1.32、node_modules复制wowjs代码 路径/node_modules/wowjs/dist/wow.js。不知道路径则查看node_modules/wowjs/package.json里面的main选项 2.1、在public文件夹创建wowjs.js文件 /public/wowjs.js export default (callthis) > { // !!// 这是…...

我们是如何实现 TiDB Cloud Serverless 的 - 成本篇
作者: shiyuhang0 原文来源: https://tidb.net/blog/fbedeea4 背景 Serverless 数据库是云原生时代的产物,它提供全托管,按需付费,自动弹性的云数据库服务,让客户免于繁重的数据库运维工作。关于 Serve…...

PCL算法汇总
参考 【2024最新版】PCL点云处理算法汇总(C长期更新版)_pcl点云聚类c-CSDN博客...
sql注入之二次注入(sqlilabs-less24)
二阶注入(Second-Order Injection)是一种特殊的 SQL 注入攻击,通常发生在用户输入的数据首先被存储在数据库中,然后在后续的操作中被使用时,触发了注入漏洞。与传统的 SQL 注入(直接注入)不同&a…...

Android compose 软键盘 遮挡对话框中TextField 输入框
在AlertDialog对话框中含有TextField输入框时,弹出软件盘会遮挡输入框 解决1: 在AndroidManifest.xml的 MainActivity中添加如下 android:windowSoftInputMode"adjustResize" 然后AlertDialog 中的modify. modify.windowInsetsP…...
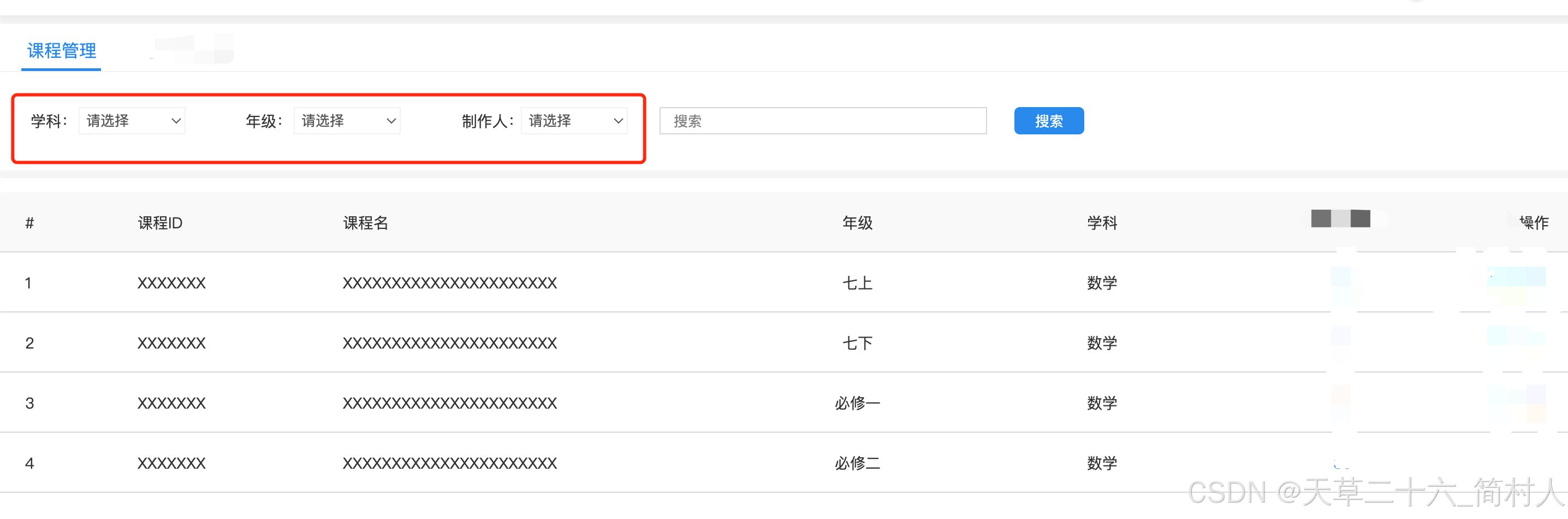
spring-data-elasticsearch 3.2.4 实现桶bucket排序去重,实现指定字段的聚合搜索
一、背景 es索引有一个文档CourseIndex,下面是示意: creatorIdgradesubjectnameno1002270英语听力课程一N00232DS91004380数学口算课程N00209DK71003480物理竞赛课程N00642XS21002280英语听力课程二N00432WS31002290英语听力课程三N002312DP5 在搜索的时候&#…...

【项目开发】分析六种常用软件架构
未经许可,不得转载。 文章目录 软件架构核心内容设计原则分层架构常见层次划分优缺点应用场景事件驱动架构核心组件优缺点应用场景微核架构核心概念优缺点应用场景微服务架构核心组件设计与实施优缺点应用场景云架构云架构模式优缺点应用场景软件架构 软件架构是指一个软件系…...

算法和程序的区别
算法(Algorithm)和程序(Program)是计算机科学中两个密切相关但不同的概念。让我们通过以下几个方面来比较它们: ### 1. 设计 vs 实现 - **算法设计(Algorithm Design)**: - **定…...

用指针遍历数组
#include<stdio.h> int main() {//定义一个二维数组int arr[3][4] {{1,2,3,4},{2,3,4,5},{3,4,5,6},};//获取二维数组的指针int (*p)[4] arr;//二维数组里存的是一维数组int[4]for (int i 0; i < 3; i){//遍历一维数组for (int j 0; j <4; j){printf("%d &…...

《Probing the 3D Awareness of Visual Foundation Models》论文解析——多视图一致性
一、论文简介 论文讨论了大规模预训练产生的视觉基础模型在处理任意图像时的强大能力,这些模型不仅能够完成训练任务,其中间表示还对其他视觉任务(如检测和分割)有用。研究者们提出了一个问题:这些模型是否能够表示物体…...

使用pip安装esp32的擦除、写入固件的esptool库
esptool库可以为esp32的开发板烧录新的固件,但是如果为了烧录固件就要装esp-idf软件包,甚至需要用make编译安装很久,实在太费时费力了! 好消息就是,esp提供了python的esptool库,这样只要使用pip安装上这个…...

传奇996_23——杀怪掉落,自动捡取,捡取动画
一、杀怪掉落 前置: 添加地图地图刷怪怪物掉落(术语叫爆率,掉落叫爆率,而且文档上叫爆率) 刷怪步骤:在\MirServer\Mir200\Envir\MonItems文件夹中建立以怪物名字为文件名的txt文件写法案例: …...

【030】基于51单片机甲醛检测报警器【Proteus仿真+Keil程序+报告+原理图】
☆、设计硬件组成:51单片机最小系统 ZE08-CH2O甲醛传感器AT24C02存储芯片LCD1602液晶显示按键设置蜂鸣器报警。 1、本设计采用STC89C52、AT89C52、AT89S52作为主控芯片; 2、采用ZE08-CH2O甲醛传感器采集环境中的甲醛浓度值,LCD1602实时显示…...

微信小程序:vant组件库安装步骤
前言:在微信小程序中引用vant组件报错,提示路径不存在,这很有可能是因为没有安装构建vant组件库导致。下面是我整理的安装vant组件库的步骤: 第一步:安装node.js(执行完第一步请重启小程序) 具体步骤请看链接:node.js…...

处理namespace问题:Namespace not specified for AGP 8.0.0
How do I fix ‘namespace not specified’ error in Android Studio? Namespace not specified for AGP 8.0.0 解决方案 <?xml version"1.0" encoding"utf-8"?> <manifest xmlns:android"http://schemas.android.com/apk/res/androi…...

C++(Qt)软件调试---内存分析工具Heob(26)
C(Qt)软件调试—内存分析工具Heob(26) 文章目录 C(Qt)软件调试---内存分析工具Heob(26)[toc]1、概述🐜2、环境配置🪲3、功能说明4、使用Heob分析qt 程序内存泄漏🦧5、使用Heob检测qt 程序野指针…...

Redis五大基本类型——String字符串命令详解(命令用法详解+思维导图详解)
目录 一、String字符串类型介绍 二、常见命令 1、SET 2、GET 3、MGET 4、MSET 使用MGET 和 使用多次GET的区别 5、DEL 6、SETNX SET、SET NX和SET XX执行流程 7、INCR 8、INCRBY 9、DECR 10、DECYBY 11、INCRBYFLOAT 12、APPEND 13、GETRANGE 14、SETRANGE …...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...


